ServletContextListener知识点

1 知识点

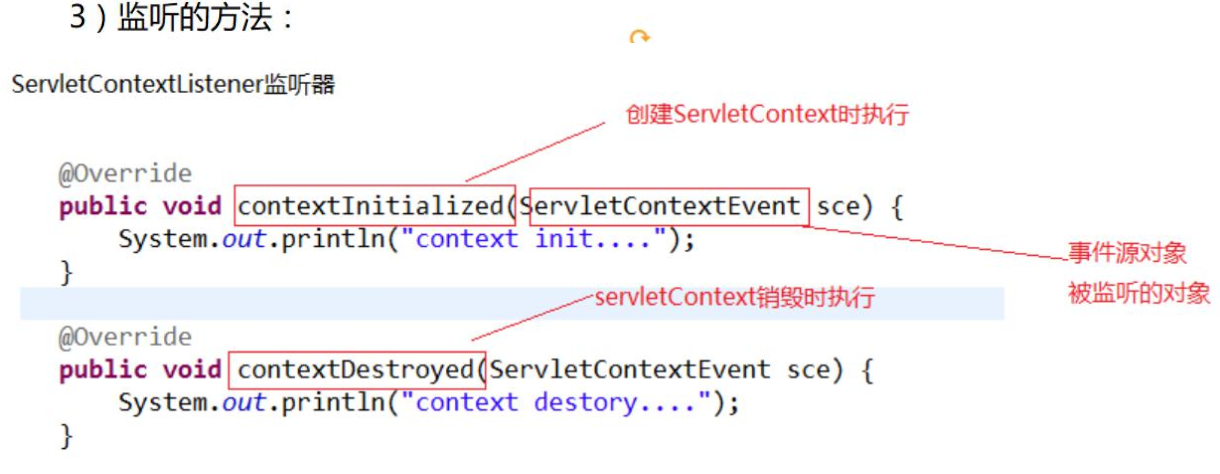
2 代码演示

import java.text.ParseException;
import java.text.SimpleDateFormat;
import java.util.Date;
import java.util.Timer;
import java.util.TimerTask;

import javax.servlet.ServletContext;
import javax.servlet.ServletContextEvent;
import javax.servlet.ServletContextListener;

public class MyServletContextListener implements ServletContextListener{

    @Override
    //监听context域对象的创建
    public void contextInitialized(ServletContextEvent sce) {
        //就是被监听的对象---ServletContext
        //ServletContext servletContext = sce.getServletContext();
        //getSource就是被监听的对象  是通用的方法
        //ServletContext source = (ServletContext) sce.getSource();
        //System.out.println("context创建了....");

        //开启一个计息任务调度----每天晚上12点 计息一次
        //Timer timer = new Timer();
        //task:任务  firstTime：第一次执行时间  period：间隔执行时间
        //timer.scheduleAtFixedRate(task, firstTime, period);
        /*timer.scheduleAtFixedRate(new TimerTask() {
            @Override
            public void run() {
                System.out.println("银行计息了.....");
            }
        } , new Date(), 5000);*/

        //修改成银行真实计息业务
        //1、起始时间： 定义成晚上12点
        //2、间隔时间：24小时
        /*SimpleDateFormat format = new SimpleDateFormat("yyyy-MM-dd hh:mm:ss");
        //String currentTime = "2016-08-19 00:00:00";
        String currentTime = "2016-08-18 09:34:00";
        Date parse = null;
        try {
            parse = format.parse(currentTime);
        } catch (ParseException e) {
            e.printStackTrace();
        }

        timer.scheduleAtFixedRate(new TimerTask() {
            @Override
            public void run() {
                System.out.println("银行计息了.....");
            }
        } , parse, 24*60*60*1000);*/

    }

    //监听context域对象的销毁
    @Override
    public void contextDestroyed(ServletContextEvent sce) {
        System.out.println("context销毁了....");

    }

}