[TJOI2010]打扫房间

题目描述

学校新建了一批宿舍，值日生小A要把所有的空房间都打扫一遍。这些宿舍的布局很奇怪，整个建筑物里所有的房间组成一个N * M的矩阵，每个房间的东南西北四面墙上都有一个门通向隔壁房间。另外有些房间是堆放杂物的，无需打扫。小A想设计若干条打扫路线，使得恰好进出每个需打扫的房间各一次，而且进出每个房间不能通过同一个门。要求每条路线都是一个闭合的环线，并且每条路线经过的房间数大于2。

如下面两图所示均为满足要求的打扫方案（灰色格子为放杂物的房间）：

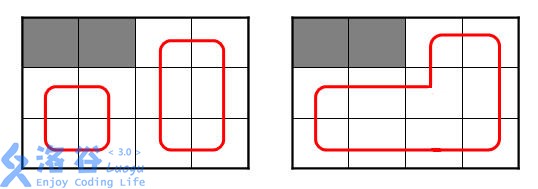
小A发现对于某些房间布局是不存在这样的满足要求的方案的。他请你写一个程序计算一下，对于一种给定的房间布局，满足要求的方案是否存在。

输入输出格式

输入格式：

输入文件的第一行是一个整数T (1 ≤ T ≤ 10)，表示该文件中一共有T组数据。接下来依次是T组数据的信息。每组数据的第一行包含两个整数N和M，接下来的N行，每行包含M个字符，表示一个房间布局。字符'.'表示该房间需要打扫，'#'表示该房间是堆放杂物的，无需打扫。

输出格式：

共输出T行，对每组数据输出一行，为"YES"或"NO"，表示打扫方案存在与否。

输入输出样例

输入样例#1：

3 10 12 4
76 60 87
78 84 84 84 81 82 72 51 77 57
85 84 62 87 88 64 81 90 80 66 88 85
65 83 63 79
2
4 5 1
4 4 2

输出样例#1：

85.64
78.00

说明

对50%的数据，3 ≤ N,M ≤ 12

对100%的数据，3 ≤ N,M ≤ 30

Solution

唔，乍看上去比较像是一个搜索题。。然后可以发现的是网络流黑白染色维护这个题并不是一件很困难的事。因为如果我们能从一个门出去，那么我们反过来走一定可以从同一个门进来。这样我们就可以这么实现，把每个黑格子与源点连流量为2的边，每个白格子与汇点连流量为2的边，黑格子和白格子之间用流量为1表示转移。这样就可以轻松实现这道题。

Code

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#define re register
#define inf 400000000
#define MAXN 10001
#define MAXM 100001
using namespace std;
int n,s,q,dis[2000011],t,l,cur[200051],m,tot,sum;
struct po
{
    int nxt,to,w;
}edge[MAXM];
int head[MAXN],dep[MAXN],num=-1;
char a[101][101];
int id[101][101],nm;
int dx[5]={0,1,0,-1,0};
int dy[5]={0,0,1,0,-1};
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline void add_edge(int from,int to,int w)
{
    edge[++num].nxt=head[from];
    edge[num].to=to;
    edge[num].w=w;
    head[from]=num;
}
inline void add(int from,int to,int w)
{
    add_edge(from,to,w);
    add_edge(to,from,0);
}
inline bool bfs()
{
    memset(dep,0,sizeof(dep));
    queue<int> q;
    while(!q.empty())
    q.pop();
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(re int i=head[u];i!=-1;i=edge[i].nxt)
        {
            int v=edge[i].to;
            if(dep[v]==0&&edge[i].w>0)
            {
                dep[v]=dep[u]+1;
                if(v==t)
                return 1;
                q.push(v);
            }
        }
    }
    return 0;
}
inline int dfs(int u,int dis)
{
    if(u==t)
    return dis;
    int diss=0;
    for(re int& i=cur[u];i!=-1;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(edge[i].w!=0&&dep[v]==dep[u]+1)
        {
            int check=dfs(v,min(dis,edge[i].w));
            if(check>0)
            {
                dis-=check;
                diss+=check;
                edge[i].w-=check;
                edge[i^1].w+=check;
                if(dis==0) break;
            }
        }
    }
    return diss;
}
inline int dinic()
{
    int ans=0;
    while(bfs())
    {
        for(re int i=0;i<=t;i++)
        cur[i]=head[i];
        while(int d=dfs(s,inf))
        ans+=d;
    }
    return ans;
}
inline void prepare()
{
	memset(head,-1,sizeof(head));
	num=-1;nm=0;
	sum=0;tot=0;
}
int main()
{
    //freopen("date.in","r",stdin);
    int T=read();
    while(T--){
    	prepare();
    	n=read();m=read();
    	for(re int i=1;i<=n;i++)
    		for(re int j=1;j<=m;j++){
    			cin>>a[i][j];
    			id[i][j]=++nm;
    			if(a[i][j]!='#') tot++;
    		}
    	s=0;t=n*m+1;
    	if(tot%2==1){cout<<"NO"<<endl;continue;}
    	for(re int i=1;i<=n;i++)
    		for(re int j=1;j<=m;j++){
    			if(i+j&1==1){
    				if(a[i][j]!='#'){
    					add(s,id[i][j],2);sum+=2;
    					for(re int k=1;k<=4;k++){
    						int lx=i+dx[k],ly=j+dy[k];
    						if(lx>=1&&lx<=n&&ly>=1&&ly<=m&&a[lx][ly]!='#')
    							add(id[i][j],id[lx][ly],1);
    					}
    				}
    			}else add(id[i][j],t,2);
    		}
    	int d=dinic();
    	if(d==sum) cout<<"YES"<<endl;
    	else cout<<"NO"<<endl;
    }
    return 0;
}