总结：Bias(偏差)，Error(误差)，Variance(方差)及CV(交叉验证)

犀利的开头

在机器学习中，我们用训练数据集去训练(学习)一个model(模型)，通常的做法是定义一个Loss function（误差函数），通过将这个Loss(或者叫error)的最小化过程，来提高模型的性能(performance)。然而我们学习一个模型的目的是为了解决实际的问题（或者说是训练数据集这个领域(field)中的一般化问题)，单纯地将训练数据集的loss最小化，并不能保证在解决更一般的问题时模型仍然是最优，甚至不能保证模型是可用的。这个训练数据集的loss与一般化的数据集的loss之间的差异就叫做generalization error=bias+variance。

作者：路小墨
链接：https://www.zhihu.com/question/27068705/answer/82132134
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

Error = Bias^2 + Variance+Noise

什么是Bias(偏差)

Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，即算法本身的拟合能力

什么是Variance(方差)

Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。反应预测的波动情况。

什么是Noise(噪声)

这就简单了，就不是你想要的真正数据，你可以想象为来破坏你实验的元凶和造成你可能过拟合的原因之一，至于为什么是过拟合的原因，因为模型过度追求Low Bias会导致训练过度，对测试集判断表现优秀，导致噪声点也被拟合进去了

简单的例子理解Bias和Variance

开枪问题

想象你开着一架黑鹰直升机，得到命令攻击地面上一只敌军部队，于是你连打数十梭子，结果有一下几种情况:

1.子弹基本上都打在队伍经过的一棵树上了，连在那棵树旁边等兔子的人都毫发无损，这就是方差小（子弹打得很集中），偏差大（跟目的相距甚远）。

2.子弹打在了树上，石头上，树旁边等兔子的人身上，花花草草也都中弹，但是敌军安然无恙，这就是方差大（子弹到处都是），偏差大（同1）。

3.子弹打死了一部分敌军，但是也打偏了些打到花花草草了，这就是方差大（子弹不集中），偏差小（已经在目标周围了）。

4.子弹一颗没浪费，每一颗都打死一个敌军，跟抗战剧里的八路军一样，这就是方差小（子弹全部都集中在一个位置），偏差小（子弹集中的位置正是它应该射向的位置）。

作者：刑无刀
链接：https://www.zhihu.com/question/20448464/answer/24397161
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

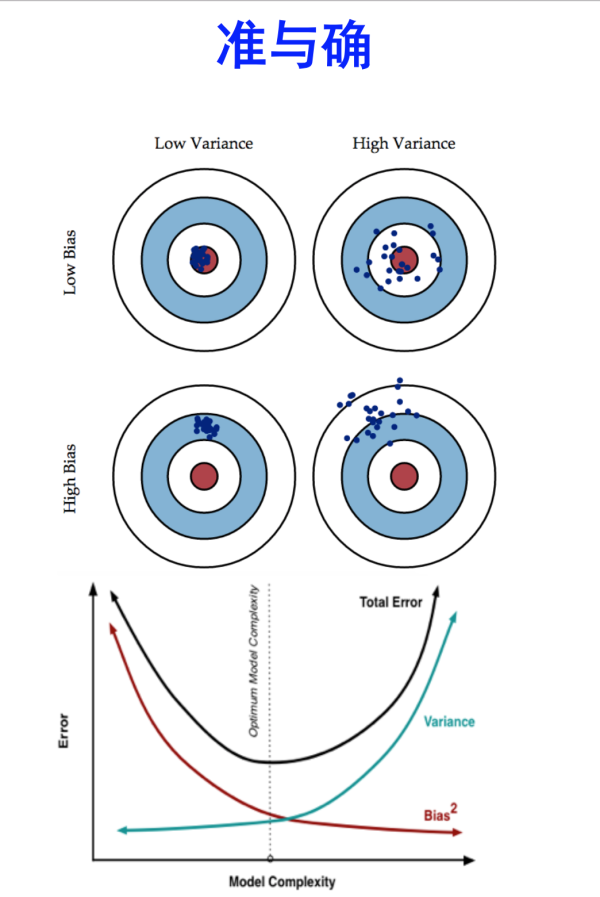
-再来个射箭问题：假设你在射箭，红星是你的目标，以下是你的射箭结果

https://www.zhihu.com/question/27068705

这里写图片描述

作者：Jason Gu
链接：https://www.zhihu.com/question/20448464
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

分析：

我们可以看到，在Low Variance的一列，数据分布是非常集中的，恩，小伙子，你的稳定性很好，方差很小，表现的很聚集。而第二列就是High Variance的一列，机智的你可能一下就看出来了，没错，飘来飘去的，非常不稳定！

看下Low Bias这一行，命中红心的次数很多对不对，说明你还是有准头的，至少偏差不算大，我要是裁判，我就不管你没射中几只箭飘到哪去了(方差大，不集中)，毕竟我看的是命中了多少(准确度)，而High Bias这一行，明显可以看出一支箭都没射中，表现很差，偏离目标好远，负分滚粗！

综合起来看，我们需要的模型最好是两个L，又准确又稳定，妥妥的，但是，这个在现实模型中是不会存在的。你只能权衡着来

Bias，Variance和Overfitting(过拟合)，Underfitting(欠拟合)

过拟合，也就是我对训练样本能够百分百命中了，超级拟合了，但是测试时候就掉链子，拟合很差，也就是我们说的泛化性能不好的问题，所以如果太追求在训练集上的完美而采用一个很复杂的模型，会使得模型把训练集里面的噪声都当成了真实的数据分布特征，从而得到错误的数据分布估计。

一句话，过拟合会出现高方差问题

欠拟合：训练样本太少，导致模型就不足以刻画数据分布了，体现为连在训练集上的错误率都很高的现象。

一句话，欠拟合会出现高偏差问题

怎么避免过拟合和欠拟合

避免欠拟合(刻画不够)

寻找更好的特征-----具有代表性的
用更多的特征-----增大输入向量的维度

避免过拟合(刻画太细，泛化太差)

增大数据集合-----使用更多的数据，噪声点比重减少
减少数据特征-----减小数据维度，高维空间密度小
正则化方法-----即在对模型的目标函数（objective function）或代价函数（cost function）加上正则项
交叉验证方法

更多方法详解请看@一只鸟的天空--机器学习中防止过拟合的处理方法

为什么要用交叉验证(Cross-Validation）

1.交叉验证,这是仅使用训练集衡量模型性能的一个方便技术，不用建模最后才使用测试集

2.Cross-validation 是为了有效的估测 generalization error(泛化误差) 所设计的实验方法，而generalization error=bias+variance

首先：bias和variance分别从两个方面来描述了我们学习到的模型与真实模型之间的差距。Bias是 “用所有可能的训练数据集训练出的所有模型的输出的平均值” 与 “真实模型”的输出值之间的差异；Variance则是“不同的训练数据集训练出的模型”的输出值之间的差异。

作者：路小墨
链接：https://www.zhihu.com/question/27068705/answer/82132134
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

可以发现，怎么来平衡Bias和Variance则成了我们最大的任务了，也就是怎么合理的评估自己模型呢？我们由此提出了交叉验证的思想,以K-fold Cross Validation(记为K-CV)为例，基本思想如下：(其他更多方法请看@bigdataage --交叉验证(Cross-Validation))

这里写图片描述

将原始数据分成K组(一般是均分),将每个子集数据分别做一次验证集,其余的K-1组子集数据作为训练集,这样会得到K个模型,用这K个模型最终的验证集的分类准确率的平均数作为此K-CV下分类器的性能指标.K一般大于等于2,实际操作时一般从3开始取,只有在原始数据集合数据量小的时候才会尝试取2. 而K-CV 的实验共需要建立 k 个models，并计算 k 次 test sets 的平均辨识率。在实作上，k 要够大才能使各回合中的训练样本数够多，一般而言 k=10 (作为一个经验参数)算是相当足够了。

看不清上面的就来一幅更简单的

这里写图片描述

每次的training_set 红色， validation_set白色，也就是说k=5的情况了

注意：交叉验证使用的仅仅是训练集！！根本没测试集什么事！很多博客都在误导！

这也就解决了上面刚开始说的Variance(不同训练集产生的差异)，Bias(所有data训练结果的平均值)这两大问题了！因为交叉验证思想集合了这两大痛点，能够更好的评估模型好坏！

说白了，就是你需要用下交叉验证去试下你的算法是否精度够好，够稳定！你不能说你在某个数据集上表现好就可以，你做的模型是要放在整个数据集上来看的！毕竟泛化能力才是机器学习解决的核心

Bias、Variance和K-fold的关系

下面解释一下Bias、Variance和k-fold的关系：k-fold交叉验证常用来确定不同类型的模型（线性、指数等）哪一种更好，为了减少数据划分对模型评价的影响，最终选出来的模型类型（线性、指数等）是k次建模的误差平均值最小的模型。当k较大时，经过更多次数的平均可以学习得到更符合真实数据分布的模型，Bias就小了，但是这样一来模型就更加拟合训练数据集，再去测试集上预测的时候预测误差的期望值就变大了，从而Variance就大了；反之，k较小时模型不会过度拟合训练数据，从而Bias较大，但是正因为没有过度拟合训练数据，Variance也较小。

作者：TANGent
链接：https://www.zhihu.com/question/27068705/answer/35286205
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

致谢

@知乎--机器学习中的Bias(偏差)，Error(误差)，和Variance(方差)有什么区别和联系？
@知乎--方差和偏差
 @bigdataage --交叉验证(Cross-Validation)
@一只鸟的天空--机器学习中防止过拟合的处理方法