BZOJ1491 洛谷2047 NOI2007 社交网络

Description：

在社交网络（social network）的研究中，我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。在一个社交圈子里有n个人，人与人之间有不同程度的关系。我 们将这个关系网络对应到一个n个结点的无向图上，两个不同的人若互相认识，则在他们对应的结点之间连接一条无向边，并附上一个正数权值c，c越小，表示两 个人之间的关系越密切。

我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度，注意到最短路径上的其他结点为s和t的联系提供了某种便利， 即这些结点对于s 和t之间的联系有一定的重要程度。我们可以通过统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。

考虑到两个结点A和B之间可能会有多条最短路径。我们修改重要程度的定义如下：

令Cs,t表示从s到t的不同的最短路的数目，Cs,t(v)表示经过v从s到t的最短路的数目；则定义

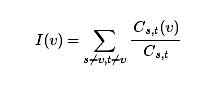
为结点v在社交网络中的重要程度。

为了使I(v)和Cs,t(v)有意义，我们规定需要处理的社交网络都是连通的无向图，即任意两个结点之间都有一条有限长度的最短路径。

现在给出这样一幅描述社交网络s的加权无向图，请你求出每一个结点的重要程度。

Input：

输入第一行有两个整数，n和m，表示社交网络中结点和无向边的数目。在无向图中，我们将所有结点从1到n进行编号。

接下来m行，每行用三个整数a, b, c描述一条连接结点a和b，权值为c的无向边。注意任意两个结点之间最多有一条无向边相连，无向图中也不会出现自环（即不存在一条无向边的两个端点是相同的结点）。

Output：

输出包括n行，每行一个实数，精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。

思路：两遍弗洛伊德，一遍求出最短路径及两点间最短路径条数，一遍求出经过某点的情况下的最短路总和。

#include<iostream>
#include<cstring>
using namespace std;
const int N = ;
int g[N][N], n, m;
long long num[N][N][N], cnt[N][N];
int main(){
    ios::sync_with_stdio(false);
    cin>>n>>m;
    int x, y, z;
    memset(g,  / , sizeof(g));
    for(int i = ; i <= m; i++){
        cin>>x>>y>>z;
        g[x][y] = g[y][x] = z;
        cnt[x][y] = cnt[y][x] = ;
    }
    for(int k = ; k <= n; k++)
      for(int i = ; i <= n; i++)
        for(int j = ; j <= n; j++)
          if(i != j && i != k && j != k){
            if(g[i][j] == g[i][k] + g[k][j])
              cnt[i][j] += cnt[i][k] * cnt[k][j];
            if(g[i][j] > g[i][k] + g[k][j])
              cnt[i][j] = cnt[i][k] * cnt[k][j], g[i][j] = g[i][k] + g[k][j];
        }
    for(int i = ; i <= n; i++)
      for(int j = ; j <= n; j++)
        if(i != j)
          for(int k = ; k <= n; k++)
            if(i != k && j != k && g[i][j] == g[i][k] + g[k][j])
              num[i][j][k] = cnt[i][k] * cnt[k][j];
   double ans;
    for(int k = ; k <= n; k++){
        ans = ;
        for(int i = ; i <= n; i++)
          for(int j = ; j <= n; j++)
            if(k != i && k != j && i != j)
              ans += double(num[i][j][k]) / double(cnt[i][j]);
        printf("%.3f\n", ans);
    }

    return ;
}