【BZOJ】3203: [Sdoi2013]保护出题人（几何+三分+特殊的技巧）

http://www.lydsy.com/JudgeOnline/problem.php?id=3203

wa无数次QAQ，犯sb错。。。。一是数组没有引用。。。二是输出转成了int（越界了sad）。。三是叉积的顺序忘记了（cross(v, w)>0的话说明v在下边啊。。。。）。。。sad。。然后提交无数次。wa了无数次。。QAQ

还有这题的思想真巧妙。。

首先看题我们得得到一个公式。

对于每一关，yi=max{(sum[i]-sum[j-1])/(x[i]+(i-j)*d)}

我一开始很好奇这是怎么来的QAQ。。想了挺久。。

我们可以将每一个僵尸的血看成是它前边所有僵尸的血加上自己的血！因为植物是一直攻击的，而僵尸的速度一定，也就是说，僵尸是从x[i]+(i-j)*d的地方走来（恰好走到门前就被打死），也就是血刚好为前边的血加上自己的血就可以看做自己的走到门前所需的血。那么因为保证不能使任何一个僵尸走上来，所以取max。

good。。

然后显然这是n^2不可过。。。。

然后这又是一个十分巧妙的地方！

我们看这个公式，是不是很像某个东西？对了，斜率！数形结合啊！

首先斜率k=(y1-y2)/(x1-x2)，看。。sum[i]可以看做y1，sum[j-1]看做y2；将除数拆开成x[i]+i*d-j*d，那么x[i]+i*d可以看做x1，j*d可以看做x2。

太神了！

而且这些值都是给定了的！

对于每一关，假设(x1, y1)是P点，(x2, y2)是Q点。P点只有唯一一个。

我们将点画到坐标系中，显然要求的max是所有的Q点到P点的斜率最大的那个Q点。。（下方的图来自hta的blog）

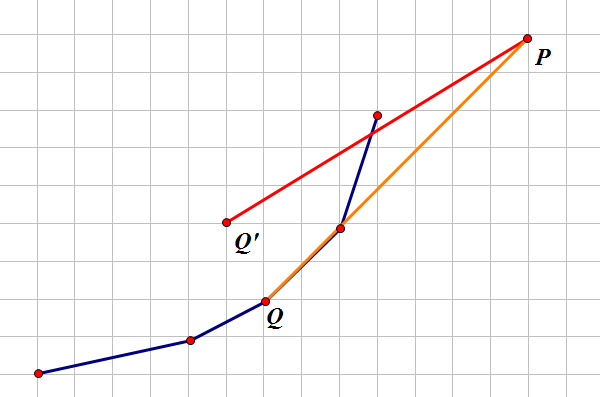
而且显然，备选的Q点应该在凸壳上。而凸壳上到P的斜率是单峰的。

那么我们可以三分凸壳，然后就行了。

还有，整数的三分不像小数的三分那样好写，整数三分的判定是(r-l>=3)，然后在求出来的[l, r]中再找一次取最大即可。

#include <cstdio>

#include <cstring>

#include <cmath>

#include <string>

#include <iostream>

#include <algorithm>

#include <queue>

using namespace std;

#define rep(i, n) for(int i=0; i<(n); ++i)

#define for1(i,a,n) for(int i=(a);i<=(n);++i)

#define for2(i,a,n) for(int i=(a);i<(n);++i)

#define for3(i,a,n) for(int i=(a);i>=(n);--i)

#define for4(i,a,n) for(int i=(a);i>(n);--i)

#define CC(i,a) memset(i,a,sizeof(i))

#define read(a) a=getint()

#define print(a) printf("%d", a)

#define dbg(x) cout << (#x) << " = " << (x) << endl

#define printarr2(a, b, c) for1(_, 1, b) { for1(__, 1, c) cout << a[_][__]; cout << endl; }

#define printarr1(a, b) for1(_, 1, b) cout << a[_] << '\t'; cout << endl

inline const long long getint() { long long r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }

inline const double max(const double &a, const double &b) { return a>b?a:b; }

inline const int min(const int &a, const int &b) { return a<b?a:b; }

const int N=100105;

const double eps=1e-8;

struct point { double x, y; }a[N], q;

double sum[N], x[N], d;

int s[N], top, n;

inline double cross(const point& a, const point& b, const point& c) { return (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y); }

inline double K(const point& a, const point& b) { return (a.y-b.y)/(a.x-b.x); }

double ifind(const point& pos) {

	int l=1, r=top, lmid, rmid;

	while(r-l>=3) {

		lmid=l+(r-l)/3;

		rmid=r-(r-l)/3;

		double k1=K(a[s[lmid]], pos), k2=K(a[s[rmid]], pos);

		if(k2>k1) l=lmid;

		else r=rmid;

	}

	double ans=0;

	for1(i, l, r) ans=max(K(pos, a[s[i]]), ans);

	return ans;

}

int main() {

	read(n); read(d);

	for1(i, 1, n) {

		read(sum[i]); read(x[i]);

		sum[i]+=sum[i-1];

		a[i].x=i*d; a[i].y=sum[i-1];

	}

	double ans=0;

	for1(i, 1, n) {

		while(top>1 && cross(a[i], a[s[top]], a[s[top-1]])>=0) --top;

		s[++top]=i;

		q.x=x[i]+i*d; q.y=sum[i];

		ans+=ifind(q);

	}

	printf("%.0lf\n", ans);

	return 0;

}

Description

Input

第一行两个空格隔开的正整数n和d，分别表示关数和相邻僵尸间的距离。接下来n行每行两个空格隔开的正整数，第i + 1行为Ai和 Xi，分别表示相比上一关在僵尸队列排头增加血量为Ai 点的僵尸，排头僵尸从距离房子Xi米处开始接近。

Output

一个数，n关植物攻击力的最小总和，保留到整数。

Sample Input

5 2
3 3
1 1
10 8
4 8
2 3

Sample Output

HINT

第一关：距离
房子3米处有一只血量3点的僵尸，植物最小攻击力为1.00000；
第二关：距离房子1米处有一只血量1点的僵尸、3米处有血量3点的僵尸，植物最小攻击力为1.33333；
第三关：距离房子8米处有一只血量10点的僵尸、10米处有血量1点的僵尸、12米处有血量3点的僵尸，植物最小攻击力为1.25000；
第四关：距离房子8米处有一只血量4点的僵尸、10米处有血量10点的僵尸、12米处有血量1点的僵尸、14米处有血量3点的僵尸，植物最小攻击力为
1.40000；第五关：距离房子3米处有一只血量2点的僵尸、5米处有血量4点的僵尸、7米处有
血量10点的僵尸、9米处有血量1点的僵尸、11米处有血量3点的僵尸，植物最小攻击力为2.28571。植物攻击力的最小总和为7.26905。

对于100%的数据， 1≤n≤10^5，1≤d≤10^12,1≤x≤ 10^12,1≤a≤10^12

Source