HDU - 6435 Problem J. CSGO (曼哈顿距离变换)

题目大意：有两类武器（主武器和副武器），每类有若干把，每把武器都有一个基础属性S，以及k个附加属性，让你选一把主武器M和一把副武器S，使得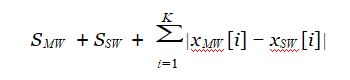最大。

显然后面的和式是一个k维的曼哈顿距离，带绝对值符号不好算，因此要想办法把绝对值去掉。由于两点任意一个维度（设其值分别为a,b）的曼哈顿距离要么是a-b，要么是b-a，符号总是相反的，因此可以二进制枚举每一维的正负号，对主武器取最大值，对副武器取最小值，两者相减就可以得到最大的曼哈顿距离。中间可能有的值不合法，但不合法的值一定不是最优值，因此可以忽略。

至于基础属性，只要对主武器加上S，对副武器减去S就行了。

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N=1e5+,inf=0x3f3f3f3f3f3f3f3fll;
 int n,m,k,a[N][],b[N][],Log[N];
 ll Sa[N][<<],Sb[N][<<];
 int main() {
     Log[]=-;
     for(int i=; i<N; ++i)Log[i]=Log[i>>]+;
     int T;
     for(scanf("%d",&T); T--;) {
         scanf("%d%d%d",&n,&m,&k);
         for(int i=; i<n; ++i) {
             scanf("%d",&a[i][k]);
             for(int j=; j<k; ++j)scanf("%d",&a[i][j]);
         }
         for(int i=; i<m; ++i) {
             scanf("%d",&b[i][k]);
             for(int j=; j<k; ++j)scanf("%d",&b[i][j]);
         }
         for(int i=; i<n; ++i) {
             for(int S=; S<(<<k); ++S)Sa[i][S]=;
             for(int j=; j<k; ++j)Sa[i][]+=a[i][j];
             Sa[i][]+=a[i][k];
         }
         for(int i=; i<m; ++i) {
             for(int S=; S<(<<k); ++S)Sb[i][S]=;
             for(int j=; j<k; ++j)Sb[i][]+=b[i][j];
             Sb[i][]-=b[i][k];
         }
         for(int S=; S<(<<k); ++S) {
             for(int i=; i<n; ++i)Sa[i][S]=Sa[i][S^(<<Log[S])]-*a[i][Log[S]];
             for(int i=; i<m; ++i)Sb[i][S]=Sb[i][S^(<<Log[S])]-*b[i][Log[S]];
         }
         ll ans=;
         for(int S=; S<(<<k); ++S) {
             ll mx=~inf,mi=inf;
             for(int i=; i<n; ++i)mx=max(mx,Sa[i][S]);
             for(int i=; i<m; ++i)mi=min(mi,Sb[i][S]);
             ans=max(ans,mx-mi);
         }
         printf("%lld\n",ans);
     }
     return ;
 }