7.6 T1 深度优先搜索（dfs）

深度优先搜索（dfs）

【题目描述】

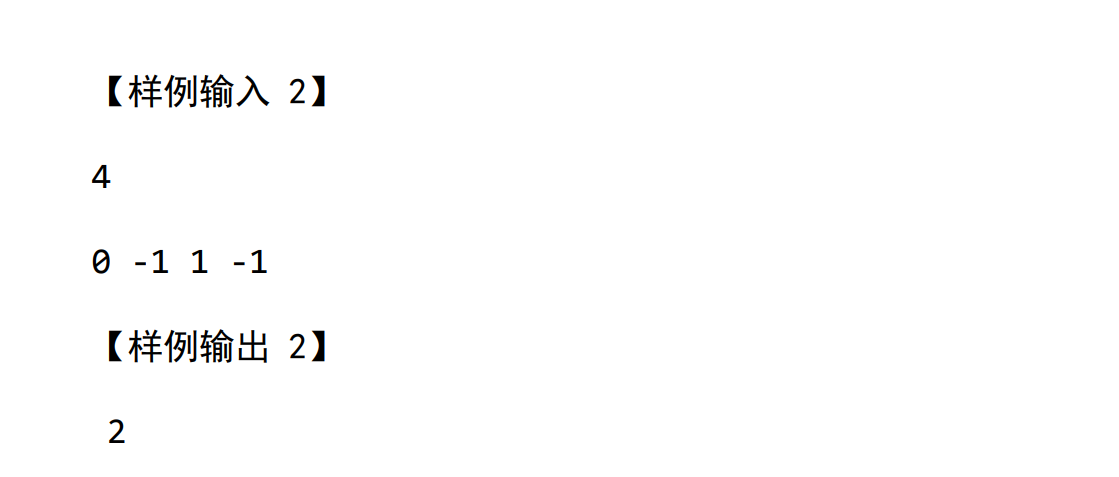
sol：50pts随便写写，就是大众分了，直接n²dpOK，100分要找点规律，需要数学头脑

官方题解

//#include <bits/stdc++.h>
//using namespace std;
//typedef long long ll;
//inline ll read()
//{
//    ll s=0;
//    bool f=0;
//    char ch=' ';
//    while(!isdigit(ch))
//    {
//        f|=(ch=='-'); ch=getchar();
//    }
//    while(isdigit(ch))
//    {
//        s=(s<<3)+(s<<1)+(ch^48); ch=getchar();
//    }
//    return (f)?(-s):(s);
//}
//#define R(x) x=read()
//inline void write(ll x)
//{
//    if(x<0)
//    {
//        putchar('-'); x=-x;
//    }
//    if(x<10)
//    {
//        putchar(x+'0'); return;
//    }
//    write(x/10);
//    putchar((x%10)+'0');
//    return;
//}
//#define W(x) write(x),putchar(' ')
//#define Wl(x) write(x),putchar('\n')
//const int N=3005;
//const ll Mod=1000000007;
//int n,a[N];
//ll dp[N][N],Sum[N];
//inline void Ad(ll &x,ll y) {x=x+y; x-=(x>=Mod)?Mod:0;}
//int main()
//{
//    freopen("dfs.in","r",stdin);
//    freopen("dfs.out","w",stdout);
//    int i,j;
//    R(n);
//    for(i=1;i<=n;i++) R(a[i]);
//    if((a[1]!=-1)&&(a[1]!=0)) return puts("0"),0;
//    dp[1][0]=1; Sum[n+1]=0; for(i=n;i>=0;i--) Ad(Sum[i],Sum[i+1]+dp[1][i]);
//    for(i=2;i<=n;i++)
//    {
//        if(a[i]!=-1) Ad(dp[i][a[i]],Sum[a[i]-1]);
//        else for(j=1;j<=n;j++) Ad(dp[i][j],Sum[j-1]);
//        for(j=n;j>=0;j--) {Sum[j]=Sum[j+1]+dp[i][j]; Sum[j]-=((Sum[j]>=Mod)?Mod:0);}
//    }
//    ll ans=0;
//    for(i=0;i<=n;i++) Ad(ans,dp[n][i]);
//    Wl(ans);
//    return 0;
//}
///*
//input
//2
//1 -1
//output
//0
//
//input
//4
//0 -1 1 -1
//output
//2
//
//input
//5
//-1 -1 -1 -1 -1
//output
//14
//*/

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll s=;
    bool f=;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<)+(s<<)+(ch^); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<)
    {
        putchar('-'); x=-x;
    }
    if(x<)
    {
        putchar(x+''); return;
    }
    write(x/);
    putchar((x%)+'');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const ll Mod=;
const int N=;
int n,a[N];
ll Jiec[N],Invj[N];
inline ll Ksm(ll x,ll y)
{
    ll ans=;
    while(y)
    {
        if(y&) ans=ans*x%Mod;
        x=x*x%Mod;
        y>>=;
    }
    return ans;
}
inline ll C(ll n,ll m)
{
    if(n<m||m<) return ;
    return Jiec[n]*Invj[m]%Mod*Invj[n-m]%Mod;
}
int main()
{
    freopen("dfs.in","r",stdin);
    freopen("dfs.out","w",stdout);
    ll i,Last,ans;
    R(n);
    for(i=;i<=n;i++) R(a[i]);
    Jiec[]=Invj[]=1ll;
    for(i=;i<=*n;i++)
    {
        Jiec[i]=Jiec[i-]*i%Mod; Invj[i]=Ksm(Jiec[i],Mod-);
    }
    if((a[]!=)&&(a[]!=-)) return puts(""),;
    a[]=; Last=ans=a[n+]=;
    for(i=;i<=n+;i++) if(a[i]!=-)
    {
        if(a[i]==) return puts(""),;
        int s=i-Last-,x=i-Last--a[i]++a[Last];
        if(x<) return puts(""),;
        ans=1ll*ans*(C(s+x,x)-C(s+x,x-a[Last]-))%Mod;
        Last=i;
    }
    ans+=(ans<)?Mod:;
    Wl(ans);
    return ;
}
/*
input
6
-1 -1 -1 -1 -1 -1
output
42
*/