LCA cogs 2450 2048 1588

t1 2450距离 链接：http://cogs.pro:8081/cogs/problem/problem.php?pid=vSNNNVqga

【题目描述】

在一个村子里有N个房子，一些双向的路连接着他们。人们总喜欢问这个“如果1想从房子A走到房子B有多远？”这个通常很难回答。但幸运的是在这个村里答案总是唯一的，自从道路修建以来这只有唯一的一条路（意思是你不能去一个地方两次）在每两座房子之间。你的工作是回答所有好奇的人。

【输入格式】

输入文件第一行有两个数n(2≤n≤10000)和m(1≤m≤20000),即房子数和问题数。后面n-1行每行由3个数构成i，j，k，由空格隔开，意思是房子i和房子j之间距离为k（0<k≤100）。房子以1到n标记。

下面m行每行有两个不同的整数i和j，你需要回答房子i和房子j之间的距离。

【输出格式】

输出有n行。每行表示个一个问题的答案。

【样例1】

输入样例1：
3 2
1 2 10
3 1 15
1 2
2 3
输出样例1：
10
25

【样例2】

输入样例2：
2 2
1 2 100
1 2
2 1
输出样例2：
100
100

思路：一道带边权的LCA，tarjan离线算法即可，将query读进来作为一种结构，同边一样记录，dfs的时候同时维护一个栈，栈元素的x为查询的from，i为边序号，维护这个栈即可，同时
　　距离dis[x]表示树根到x的距离，每次递归处理，ans[q[i].id]即为第几次询问的答案， 理解ans = dis_x + dis_y - 2 * dis_LCA，通过函数找到x和y的LCA
代码

 #define _CRT_SECURE_NO_WARNINGS
 #include "iostream"
 #include "cstdio"
 #include "cstring"
 #define maxn 10010
 using namespace std;
 int n, m, from, to, k;
 struct Edge
 {
     int to, val, pre;
 }e[maxn << ];

 struct query
 {
     int to, id, pre;
 }q[maxn << ];

 struct AA
 {
     int x, i;
 }a[maxn];

 int lastE[maxn] = {  };
 int lastQ[maxn] = {  };
 int p[maxn] = {  };
 int dis[maxn], anc[maxn], ans[maxn << ];
 bool vis[maxn << ] = {  };
 int cnt = , cnt1 = , cnt2 = , top = ;

 void inserte(int from, int to, int val)
 {
     e[++cnt1].to = to;
     e[cnt1].val = val;
     e[cnt1].pre = lastE[from];
     lastE[from] = cnt1;
 }

 void insertq(int from, int to, int i)
 {
     q[++cnt2].to = to;
     q[cnt2].id = i;
     q[cnt2].pre = lastQ[from];
     lastQ[from] = cnt2;
 }

 int findRoot(int x)
 {
     static int y, root;
     root = anc[x];
     while (anc[root] != root)
         root = anc[root];
     while (anc[x] != x)
     {
         y = anc[x];
         anc[x] = root;
         x = y;
     }
     return root;
 }

 void dfs(int x)
 {
     int y, i;
     a[++top].x = x;
     a[top].i = lastE[x];
     while (top)
     {
         x = a[top].x;
         i = a[top].i;
         if (e[i].to == p[x])
             i = e[i].pre;
         if (i)
         {
             a[top].i = e[i].pre;
             y = e[i].to;
             p[y] = x;
             dis[y] = dis[x] + e[i].val;
             a[++top].x = y;
             a[top].i = lastE[y];
             anc[y] = y;
          }
         else
         {
             vis[x] = ;
             for (int i = lastQ[x]; i; i = q[i].pre)
             {
                 y = q[i].to;
                 if (vis[y])
                 {
                     ans[q[i].id] = dis[x] + dis[y] - (dis[findRoot(y)] << );
                 }
             }
             anc[x] = p[x];
             top--;
         }
     }
 }

 int main()
 {
     freopen("distance.in", "r", stdin);
     freopen("distance.out", "w", stdout);
     scanf("%d%d", &n, &m);
     for (int i = ; i < n - ; i++)
     {
         scanf("%d %d %d", &from, &to, &k);
         inserte(from, to, k);
         inserte(to, from, k);
     }
     for (int i = ; i < m; i++)
     {
         scanf("%d %d", &from, &to);
         insertq(from, to, i);
         insertq(to, from, i);
     }
     dis[] = p[] = ;
     dfs();

     for (int i = ; i < m; i++)
         printf("%d\n", ans[i]);
     return ;
 }

t2 cogs 1588 题目链接：http://cogs.pro:8081/cogs/problem/problem.php?pid=vxmxQkgUU

【题目描述】

农夫约翰有N（2<=N<=40000）个农场，标号1到N。M（2<=M<=40000）条的不同的垂直或水平的道路连结着农场，道路的长度不超过1000.这些农场的分布就像下面的地图一样，图中农场用F1..F7表示：

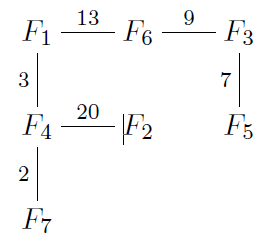
每个农场最多能在东西南北四个方向连结4个不同的农场。此外，农场只处在道路的两端。道路不会交叉而且每对农场间有且仅有一条路径。邻居鲍伯要约翰来导航，但约翰丢了农场的地图，他只得从电脑的备份中修复率。每一条道路的信息如下：

从农场23往南经距离10到达农场17

从农场1往东经距离7到达农场17

. . .

最近美国过度肥胖非常普遍。农夫约翰为了让他的奶牛多做运动，举办了奶牛马拉松。马拉松路线要尽量长。

奶牛们拒绝跑马拉松，因为她们悠闲的生活无法承受约翰选择的如此长的赛道。因此约翰决心找一条更合理的赛道。他打算咨询你。读入地图之后会有K个问题，每个问题包括2个整数，就是约翰感兴趣的2个农场的编号，请尽快算出这2个农场间的距离。

【输入格式】

第1行：两个分开的整数N和M。

第2到M+1行：每行包括4个分开的内容，F1,F2,L,D分别描述两个农场的编号，道路的长度，F1到F2的方向N,E,S,W。

第2+M行：一个整数K（1<=K<=10000）.

第3+M到2+M+K行：每行输入2个整数，代表2个农场。

【输出格式】

对每个问题，输出单独的一个整数，给出正确的距离。

【样例输入】

7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S
3
1 6
1 4
2 6

【样例输出】

13
3
36

【提示】

农场2到农场6有20+3+13=36的距离。

同t1，读入的时候读方向但是忽略即可。

代码：

 #define _CRT_SECURE_NO_WARNINGS
 #include "iostream"
 #include "cstdio"
 #include "cstring"
 #define maxn 40010
 using namespace std;
 int n, m, from, to, k, sumQ;
 struct Edge
 {
     int to, val, pre;
 }e[maxn << ];

 struct query
 {
     int to, id, pre;
 }q[maxn << ];

 struct AA
 {
     int x, i;
 }a[maxn];

 int lastE[maxn] = {  };
 int lastQ[maxn] = {  };
 int p[maxn] = {  };
 int dis[maxn], anc[maxn], ans[maxn << ];
 bool vis[maxn << ] = {  };
 int cnt = , cnt1 = , cnt2 = , top = ;

 void inserte(int from, int to, int val)
 {
     e[++cnt1].to = to;
     e[cnt1].val = val;
     e[cnt1].pre = lastE[from];
     lastE[from] = cnt1;
 }

 void insertq(int from, int to, int i)
 {
     q[++cnt2].to = to;
     q[cnt2].id = i;
     q[cnt2].pre = lastQ[from];
     lastQ[from] = cnt2;
 }

 int findRoot(int x)
 {
     static int y, root;
     root = anc[x];
     while (anc[root] != root)
         root = anc[root];
     while (anc[x] != x)
     {
         y = anc[x];
         anc[x] = root;
         x = y;
     }
     return root;
 }

 void dfs(int x)
 {
     int y, i;
     a[++top].x = x;
     a[top].i = lastE[x];
     while (top)
     {
         x = a[top].x;
         i = a[top].i;
         if (e[i].to == p[x])
             i = e[i].pre;
         if (i)
         {
             a[top].i = e[i].pre;
             y = e[i].to;
             p[y] = x;
             dis[y] = dis[x] + e[i].val;
             a[++top].x = y;
             a[top].i = lastE[y];
             anc[y] = y;
         }
         else
         {
             vis[x] = ;
             for (int i = lastQ[x]; i; i = q[i].pre)
             {
                 y = q[i].to;
                 if (vis[y])
                 {
                     ans[q[i].id] = dis[x] + dis[y] - (dis[findRoot(y)] << );
                 }
             }
             anc[x] = p[x];
             top--;
         }
     }
 }

 int main()
 {
     freopen("dquery.in", "r", stdin);
     freopen("dquery.out", "w", stdout);
     char c;
     scanf("%d%d", &n, &m);
     for (int i = ; i < m; i++)
     {
         scanf("%d %d %d %c", &from, &to, &k, &c);
         inserte(from, to, k);
         inserte(to, from, k);
     }
     scanf("%d", &sumQ);
     for (int i = ; i < sumQ; i++)
     {
         scanf("%d %d", &from, &to);
         insertq(from, to, i);
         insertq(to, from, i);
     }
     dis[] = p[] = ;
     dfs();

     for (int i = ; i < sumQ; i++)
         printf("%d\n", ans[i]);
     return ;
 }

t3 cogs

2084. [SYOI 2015] Asm.Def的基本算法

链接：http://cogs.pro:8081/cogs/problem/problem.php?pid=vyiJNVaUq

【题目描述】

“有句美国俗语说，如果走起来像鸭子，叫起来像鸭子，那就是一只鸭子。”斯科特·华莱士看着Asm.Def面前屏幕上滚动的绿色字符，若有所思地说。

“什么意思？”

“你的数据。看上去是一棵树。”

“按照保密条令，我什么也不说这是最好的——但见你这么热情，一句话不说也不好。”Asm.Def停下手中的快速数论变换，“确实是树。”

“然后你怎么算出来目标的位置？”

“都需要按照基本算法，按照图论的那一套理论，去产生。听说过LCA吗？不是那个印度飞机，我是说最近公共祖先……

Asm.Def通过分析无线电信号得到了一棵有n个节点，以1为根的树。除1之外，节点i的父亲是p_i。节点带有权值，节点i的权值是w_i。

我们定义某点的祖先为从根到它路径上的所有点（包括它本身），而两个节点a、b的最近公共祖先是某个点p，使得p同时是a、b的祖先，而且p离根最远。

Asm.Def想要求出

（文字：∑∑w_i*w_j*w_LCA(i,j)），

其中LCA(i,j)是i、j的最近公共祖先，他认为这个值至关重要。由于这个值可能很大，Asm.Def只需要知道它模1,000,000,007（即10^9+7）的结果。

【输入格式】

第1行两个整数：n和w_1.

第2行到第n行，第i行有两个整数p_i和w_i。

【输出格式】

一行一个整数，即答案模1,000,000,007的值。

【样例输入】

2 2
1 1

【样例输出】

17

【提示】

1×1×1+1×2×2+2×1×2+2×2×2=17。

对于30%的数据，n<=100，w_i<=10。

对于60%的数据，n<=1000，w_i<=1000.

对于100%的数据，1<=n<=10^5，0<=w_i<=10^9，1<=p_i<i.

思路：递归遍历，以每个节点为一个根 为单位，维护以此节点为根的子树的权值sum，乘积求和，见注释

代码：

 #define _CRT_SECURE_NO_WARNINGS
 #include "iostream"
 #include "cstdio"
 #include "cstring"

 #define ll long long
 #define maxn 100100
 using namespace std;

 struct Edge
 {
     ll to, pre;
     Edge() :to(), pre() {};
 }e[maxn << ];
 bool vis[maxn << ];
 int prt[maxn], n, w[maxn], last[maxn << ];
 int cnt = ;
 ll sum = ;
 int s[maxn];                                          //以x为根的点的权值和
 //int sz[maxn];                                         //子孙节点个数

 void insert(int from, int to)
 {
     e[++cnt].to = to;
     e[cnt].pre = last[from];
     last[from] = cnt;
 }

 void dfs(int x)
 {
     //sz[x] = 1;                                        //从x开始，子孙节点个数为1
     s[x] = w[x];                                      //包含自己，子节点权值和为w_x
     int y;
     for (int i = last[x]; i; i = e[i].pre)
     {
         y = e[i].to;
         if (y == prt[x])
             continue;
         prt[y] = x;
         dfs(y);
         s[x] = (s[x] + s[y]) % ;             //回溯后，子节点和累加上来
         //sz[x] += sz[y];                               //子节点个数累加
     }

     ll ss = s[x], tmp = ;
     for (int i = last[x]; i; i = e[i].pre)
     {
         y = e[i].to;
         if (y == prt[x])
             continue;
         //ss-s_y即为除了y和它的子节点权值和 其余节点的权值和，乘积满足Σwi*wj
         tmp = (tmp + ((ll)s[y] * ((ss - s[y] + ) % ) % )) % ;
         //每个乘积会被算两次但父节点和子节点不会，因此再加上s_y * wx
         tmp = (tmp + ((ll)s[y] * w[x] % )) % ;
     }
     //对每个x，都有i==j的时候，x和自己的乘积以及LCA也是它自己
     tmp = (tmp + ((ll)w[x] * w[x] % )) % ;
     //前边只有wi wj，统一乘wLCA
     tmp = ((ll)tmp * w[x]) % ;
     sum = (sum + tmp) % ;
 }

 int main()
 {
     freopen("asm_algo.in", "r", stdin);
     freopen("asm_algo.out", "w", stdout);
     int x, y;
     scanf("%d %d", &n, &w[]);
     for (int i = ; i <= n; i++)
     {
         scanf("%d %d", &x, &y);
         w[i] = y;
         insert(x, i);
     }

     dfs();
     printf("%lld\n", sum);
     return ;
 }