KMeans聚类

　　常用的聚类方法：

　　①分裂方法：

　　K-Means算法(K-平均)、K-MEDOIDS算法(K-中心点)、CLARANS算法(基于选择的算法)

　　②层次分析方法：

　　BIRCH算法(平衡迭代规约和聚类)、CURE算法(代表点聚类)、CHAMELEON算法(动态模型)

　　③基于密度的方法：

　　DBSCAN(基于高密度连接区域)、DENCLUE算法(密度分布函数)、OPTICS算法(对象排序识别)

　　④基于网格的方法：

　　STING算法(统计信息网络)、CLIOUE算法(聚类高维空间)、WAVE-CLUSTRE(小波变换)

　　⑤基于模型的方法：

　　统计学方法、神经网络方法

　　其中Kmeans、K中心点、系统聚类比较常用。

　　KMeans：K-均值聚类也叫快速聚类法，在最小化误差函数的基础上将数据划分为预定的类数K。该算法原理简单并便于处理大量的数据。

　　K中心点：K-均值算法对孤立点的敏感性，K-中心点算法不采用簇中对象的平均值作为簇中心，而选用簇中离平均值最近的对象作为簇中心。

　　系统聚类：系统聚类也叫多层次聚类，分类的单位由高到低呈树形结构，且所处的位置越低，其所包含的对象就越少，但这些对象间的共同特征越多。该聚类方法只适合在小数据量的时候使用，数据量大的时候处理速度会非常慢。

KMeans聚类

　　K-Means：在最小化误差函数的基础上将数据划分为预定的类数K，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。

算法描述

　　①从N个样本数据中随机选取K个对象作为初始的聚类中心。

　　②分别计算每个样本到各个聚类中心的距离，将对象分配到距离最近的聚类中。

　　③所有对象分配完成后，重新计算K个聚类的中心。

　　④与前一次计算得到的K个聚类中心比较，如果聚类中心发生变化，转第②步。

　　⑤当质心不发生变化时停止并输出聚类结果。

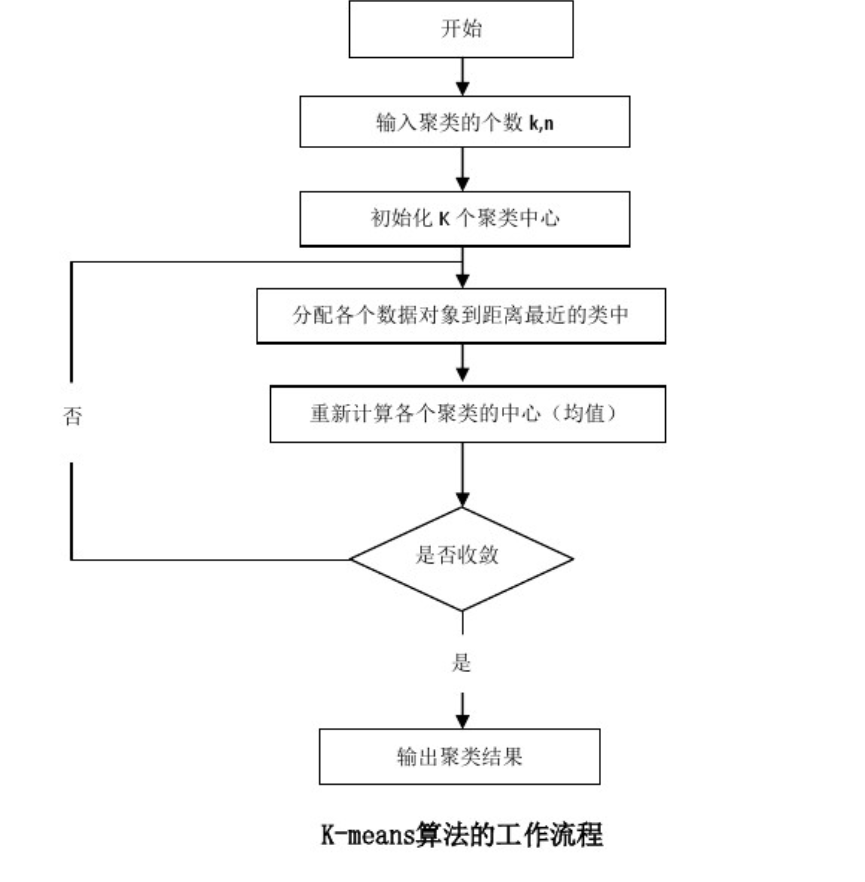
　　聚类的结果可能依赖于初始聚类中心的随机选择，可能使得结果严重偏离全局最优分类。在实践中为了得到较好的结果，通常以不同的初始聚类中心，多次运行K-Means算法。在所有对象分配完成后，重新计算K个聚类的中心时，对于连续数据聚类中心取该簇的均值。

数据类型与属性度量

　　对于连续属性，要先对各属性值进行0-均值规范，再进行距离的计算。K-Means 聚类算法中，一般需要度量样本之间的距离、样本与簇之间的距离以及簇与簇之间的距离。
　　样本之间的相似性最常用的是欧几里得距离、曼哈顿距离和闵可夫斯基距离。
　　样本与簇之间的距离可以用样本到簇中心的距离$d\left(e_{i,}, x\right)$
　　簇与簇之间的距离可以用簇中心的距离$d\left(e_{i}, e_{j}\right)$

　　　　用p个属性来表示n个样本的数据矩阵：$$\left[\begin{array}{ccc}{x_{11}} & {\cdots} & {x_{1 p}} \\ {\vdots} & {} & {\vdots} \\ {x_{n 1}} & {\cdots} & {x_{n p}}\end{array}\right]$$

　　　　欧几里得距离的计算公式为：$$d(i, j)=\sqrt{\left(x_{i 1}-x_{j 1}\right)^{2}+\left(x_{i 2}-x_{j 2}\right)^{2}+\cdots+\left(x_{i p}-x_{j p}\right)^{2}}$$

　　　　曼哈顿距离的计算公式为：$$d(i, j)=\left|x_{i+}-x_{j 1}\right|+\left|x_{2}-x_{j 2}\right|+\cdots+\left|x_{i p}-x_{i p}\right|$$

　　　　闵可夫斯基距离的计算公式为：$$d(i, j)=\sqrt[q]{\left|\left(x_{i 1}-x_{j 1} |\right)^{q}+\left(\left|x_{i 2}-x_{j 2}\right|\right)^{q}+\cdots+\left(\left|x_{i p}-x_{j p}\right|\right)^{q}\right.}$$

　　　　q为正整数，q=1时为曼哈顿距离；q=2时为欧几里得距离。

　　对于文档数据，使用余弦相似性度量，先将文档数据整理成文档一词矩阵格式。

　　　　两个文档之间的相似度的计算公式为：$d(i, j)=\cos (i, j)=\frac{\vec{i} g \vec{j}}{|\vec{i}| g|\vec{j}|}$

目标函数

　　使用误差平方和SSE(残差平方和)作为度量聚类质量的目标函数，对于两种不同的聚类结果，可选择误差平方和较小的分类结果。

　　连续属性的SSE计算公式为：$$S S E=\sum_{i=1}^{K} \sum_{x \in E_{i}} \operatorname{dist}\left(e_{i,} x\right)^{2}$$

　　文档数据的SSE计算公式为：$$S S E=\sum_{i=1}^{K} \sum_{x \in E_{i}} \cos i n e\left(e_{i}, x\right)^{2}$$

　　簇$E_{i}$的聚类中心$e_{i}$的计算公式为：$$e_{i}=\frac{1}{n_{i}} \sum_{\dot{x} \in E_{i}} x$$

　　$K$表示聚类簇的个数，$E_{i}$表示第$i$个簇，$x$表示样本，$e_{i}$表示聚类中心，$n$表示数据集中样本的个数，$n_{i}$表示第$i$个簇中样本的个数。

例子

　　根据顾客的一些消费行为特性数据，将顾客进行聚类，并评价不同顾客群体的价值。

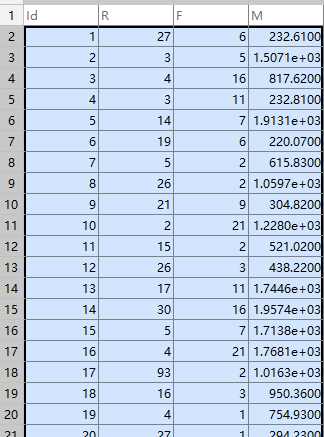
　　采用K-Means聚类算法，设定聚类个数K为3，最大迭代次数为500次，距离函数取欧氏距离。

%% 使用K-Means算法聚类消费行为特征数据
clear ;
% 参数初始化
inputfile = '../data/consumption_data.xls'; % 销量及其他属性数据
k = ; % 聚类的类别
iteration = ; % 聚类最大循环次数
distance = 'sqEuclidean'; % 距离函数
%% 读取数据
[num,txt]=xlsread(inputfile);
data = num(:,:end);
%% 数据标准化
data = zscore(data);
%% 调用kmeans算法
opts = statset('MaxIter',iteration);
[IDX,C,~,D] = kmeans(data,k,'distance',distance,'Options',opts);
%% 打印结果
for i=:k
   disp(['第' num2str(i) '组聚类中心为：']);
   disp(C(i,:));
end
disp('K-Means聚类算法完成！');

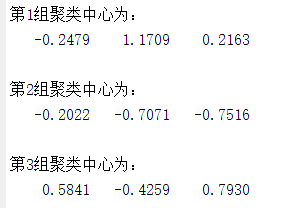
　　计算得到聚类中心为：