BZOJ1005--[HNOI2008]明明的烦恼(树的prufer编码)
1005: [HNOI2008]明明的烦恼
Time Limit: 1 Sec Memory Limit: 162 MB
Submit: 5768 Solved: 2253
[Submit][Status][Discuss]
Description
自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1
Output
一个整数,表示不同的满足要求的树的个数,无解输出0
Sample Input
1
-1
-1
Sample Output
HINT
两棵树分别为1-2-3;1-3-2
转自怡红公子(http://www.cnblogs.com/noip/archive/2013/03/10/2952520.html)----
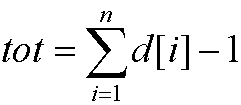
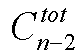 种插法;
种插法;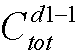 种插法;
种插法;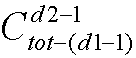 种插法;
种插法;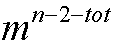 ;
;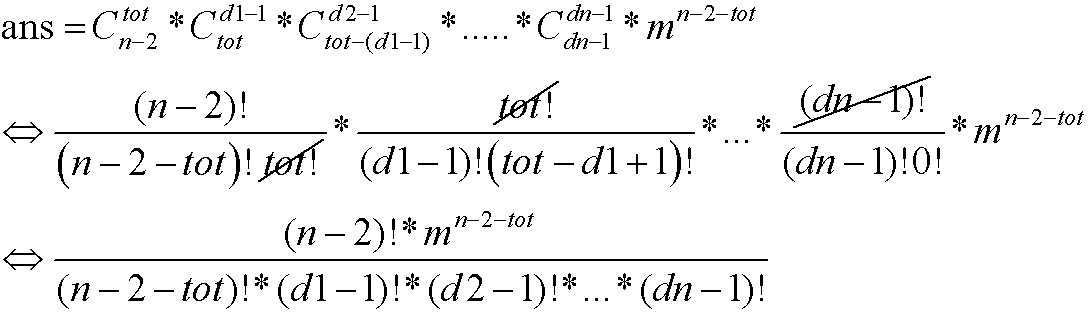
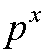 ,其中
,其中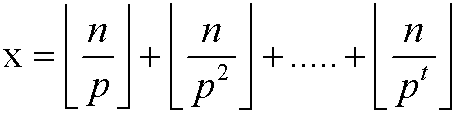 且
且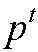 <n
<n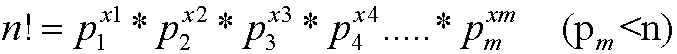
BZOJ1005--[HNOI2008]明明的烦恼(树的prufer编码)的更多相关文章
- bzoj 1005: [HNOI2008]明明的烦恼 树的prufer序列+万进制
题目传送门 思路: 这道题需要前置知识prufer编码,这篇博客对prufer编码和这道题的分析写的很好. 这里主要讲一些对大数阶乘的分解,一个办法当然是用高精度,上面这篇博客用的是java,还有一个 ...
- bzoj1005: [HNOI2008]明明的烦恼(prufer+高精度)
1005: [HNOI2008]明明的烦恼 题目:传送门 题解: 毒瘤题啊天~ 其实思考的过程还是比较简单的... 首先当然还是要了解好prufer序列的基本性质啦 那么和1211大体一致,主要还是利 ...
- bzoj1005 [HNOI2008]明明的烦恼
1005: [HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 3032 Solved: 1209 Description ...
- [BZOJ1005] [HNOI2008] 明明的烦恼 (prufer编码)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- [bzoj1005][HNOI2008][明明的烦恼] (高精度+prufer定理)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- 【prufer编码+组合数学】BZOJ1005 [HNOI2008]明明的烦恼
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣...... 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Solution 这 ...
- BZOJ1005:[HNOI2008]明明的烦恼(组合数学,Prufer)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- bzoj1005: [HNOI2008]明明的烦恼 prufer序列
https://www.lydsy.com/JudgeOnline/problem.php?id=1005 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的 ...
- [bzoj1005][HNOI2008]明明的烦恼-Prufer编码+高精度
Brief Description 给出标号为1到N的点,以及某些点最终的度数,允许在 任意两点间连线,可产生多少棵度数满足要求的树? Algorithm Design 结论题. 首先可以参考这篇文章 ...
- BZOJ1005 HNOI2008明明的烦恼(prufer+高精度)
每个点的度数=prufer序列中的出现次数+1,所以即每次选一些位置放上某个点,答案即一堆组合数相乘.记一下每个因子的贡献分解一下质因数高精度乘起来即可. #include<iostream&g ...
随机推荐
- Elastic Search快速上手(3):搜索
前言 存储好数据之后,便可通过RESTful API进行搜索. 详细文档可参考: --简单搜索https://www.elastic.co/guide/cn/elasticsearch/guide/c ...
- idea插件,配置
1.插件 2.配置 1.去除double shift 全局搜索的功能,反正不符合我的习惯 Help -> Find Action 搜索 registry ,勾选 double.click.ha ...
- winfrom_关于打印小票
1.使用的是PrintDocument控件,在工具箱 ,将其托到窗体上: 2. private void btnprint_Click(object sender, EventArgs e) { p ...
- Oracle 分页语句
** 写法1 :采用 ROWNUM的伪列: --查询10到20之间的数据 -- SELECT * FORM ( -- SELECT * , ROWNUM rn FROM TABLE_NAME -- W ...
- c++11 用户定义字面量
c++11 用户定义字面量 #define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <string> #inc ...
- 微信小程序带参数生成二维码
wx.request({ url: 'https://api.weixin.qq.com/cgi-bin/token', header: { 'content-type': 'application/ ...
- Oracle数据库(实例)删除用户和表空间
删除用户drop user IMPLOCAL cascade; 删除表空间drop tablespace IMPLOCAL including contents and datafiles casca ...
- jQuery EasyUI 数据网格
jQuery EasyUI 数据网格 - 转换 HTML 表格为数据网格 本节将介绍jQuery EasyUI数据网格的运用,主要内容为如何将HTML表格转换为数据网格. 本实例演示如何转换表格(ta ...
- kbmMW Scheduler.InAMoment用法
kbmMW Scheduler提供了一个方法InAMoment,由于没有找到调用的例子,只好查看代码,原来这个方法与RunNow差不多,是立即执行一个方法,并且在主线程中. Scheduler.InA ...
- Flask+gevent-websocket模块实现websocket
后端代码: from flask import Flask,request from geventwebsocket.handler import WebSocketHandler from geve ...
