整数划分——区间dp（石子合并）

这不是将一个数以一来划分，而是把一个整数以位来划分

题目描述

如何把一个正整数N（N长度<20）划分为M（M>1）个部分，使这M个部分的乘积最大。N、M从键盘输入，输出最大值及一种划分方式。

输入格式

第一行一个正整数T(T<=10000)，表示有T组数据。

接下来T行每行两个正整数N，M。

输出格式

对于每组数据

第一行输出最大值。

第二行输出划分方案，将N按顺序分成M个数输出，两个数之间用空格格开。

样例

样例输入

1
199 2

样例输出

171
19 9

这是递归思想，动态规划是正向的，而判断后是逆向的，输出时运用回溯，达到正向输出的目的
以下是代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
unsigned long long t,n[21],n2,n3[21][21],x,son[1000][1000],f[21][21],m;//数据极大，用无符号长整型
string n1;
int printf1(int a,int b)//输出函数，回溯
{
    if(b==0)return 0;
    printf1(son[a][b],b-1);
    for(int i=son[a][b]+1;i<=a;i++)
        cout<<n[i];
    cout<<" ";
}
int main()
{
    cin>>t;
    for(int l=1;l<=t;l++)
    {
        memset(n,0,sizeof(n));
        memset(son,0,sizeof(son));
        cin>>n1>>m;
        n2=n1.length();
        for(int i=0;i<=n2;i++)
            for(int j=0;j<=n2;j++)
            {
                f[i][j]=0;
                //n3[i][j]=1;
            }
        f[0][0]=1;
        for(int i=1;i<=n2;i++)
        {
            n[i]=n1[i-1]-'0';
            //cout<<n[i];
        }
        for(int i=1;i<=n2;i++)
        {
            x=n[i];
            for(int j=i;j<=n2;j++)
            {
                n3[i][j]=x;
                x*=10;
                x+=n[j+1];
                //cout<<n3[i][j]<<" "<<i<<" "<<j<<endl;
            }
        }
        for(int i=1;i<=n2;i++)
        {
            for(int j=1;j<=m&&j<=i;j++)
            {
                for(int k=1;k<=i;k++)
                {
                    if(f[i][j]<f[k-1][j-1]*n3[k][i])
                    {
                        f[i][j]=f[k-1][j-1]*n3[k][i];
                        //cout<<f[i][j];
                        son[i][j]=k-1;//记录分割点
                    }

                }
            }
        }
        cout<<f[n2][m]<<endl;
        if(m==n2)//特判，防止输出紊乱
            for(int i=1;i<=n2;i++)
                cout<<n[i]<<" ";
        else printf1(n2,m);
        cout<<endl;
    }
}

 石子合并

题目描述

在一个园形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出1个算法,计算出将N堆石子合并成1堆最大得分.

输入格式

数据的第1行试正整数N,1≤N≤2000,表示有N堆石子.第2行有N个数,分别表示每堆石子的个数.

输出格式

输出共1行,最大得分

样例

样例输入

4
4 4 5 9

样例输出

54
最终一堆一定是前一次合并后，剩下的两堆相加的最优解。

状态转移方程
设t[i,j]表示从第i堆到第j堆石子数总和。
Fmax(i,j)表示将从第i堆石子合并到第j堆石子的最大的得分
Fmin(i,j)表示将从第i堆石子合并到第j堆石子的最小的得分（看题意要求没）

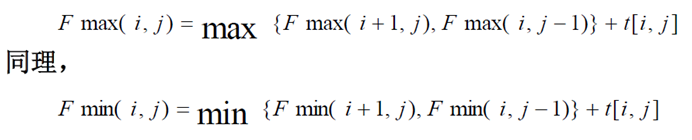
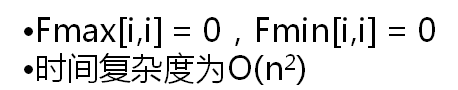
附上代码

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int n,m[4001],m1[4001][4001],f[4001][4001],x,ma;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>m[i];
    }
    for(int i=1;i<=n;i++)
    {
        m[i+n]=m[i];
    }
    for(int i=1;i<=2*n-1;i++)
    {
        x=m[i];
        for(int j=i+1;j<=2*n-1;j++)
        {
            x+=m[j];
            m1[i][j]=x;
        }
    }
    for(int i=2*n-1;i>=1;i--)
    {
        for(int j=i;j<=2*n-1;j++)
        {
            f[i][j]=max(f[i+1][j],f[i][j-1])+m1[i][j];
        }
    }
    for(int i=1;i<=n;i++)
    {
        if(ma<f[i][i+n-1])ma=f[i][i+n-1];
    }
    cout<<ma;
}