[论文翻译] 分布式训练 Parameter Sharding 之 Google Weight Sharding

[论文翻译] 分布式训练 Parameter sharding 之 Google Weight Sharding

目录

• [论文翻译] 分布式训练 Parameter sharding 之 Google Weight Sharding
• 0x00 摘要
• 0x01 引文
• 0x02 XLA背景知识
  • 2.1 All-reduce.
  • 2.2 算子融合
• 0x03 权重更新分片
  • 3.1 All-reduce分解
  • 3.2 挑战
• 0x04 图转换
  • 4.1 分片表示
    • 4.1.1 数据格式化
    • 4.1.2 Non-elementwise 算子
  • 4.2 训练计算图转换
    • 4.2.1 循环外放置
    • 4.2.2 内存节省
• 0x05 高效通信
  • 5.1 数据融合
  • 5.2 利用网络带宽
    • 5.2.1 部分分片（Partial sharding）
    • 5.2.2 批量处理通信算子(Batched communication operators)
• 0xFF 参考

0x00 摘要

本系列会以5～6篇文章，介绍parameter sharding。Parameter sharding 就是把模型参数等切分到各个GPU之上。我们会以 Google，微软和Facebook的论文，博客以及代码来进行分析。

本文以Google 论文 Automatic Cross-Replica Sharding of Weight Update in Data-Parallel Training 为主来进行分析。这里并不会逐字分析，而是选择了一些重点，并且争取加入笔者自己的理解。

与前一篇微软论文相比，Google 这篇论文会对一些实现细节有更深入的讨论，我们可以两篇论文结合起来思考。

本系列其他文章如下：

[源码解析] PyTorch 分布式之 ZeroRedundancyOptimizer

[论文翻译] 分布式训练 Parameter sharding 之 ZeRO

0x01 引文

因为其简单高效，所以数据并行是最常用的同步分布式训练策略。参与数据并行训练的设备称为副本（replicas），所有副本上都运行相同训练程序，这个训练程序包含整个神经网络，但是每个副本接收每个批次训练数据的不同分区。副本使用自己得到的训练数据计算其局部梯度，然后进行彼此通信以获得合并的梯度，并用这个梯度对本地副本的权重变量应用相同的更新。因为权重和梯度并没有按照某一个维度进行分区，因此需要在所有副本上进行重复的权重更新计算。进而我们知道，在每个副本上的权重更新成本是恒定的，即使添加了更多设备以减少每个副本的批处理大小，这个更新成本也不会变化（就是模型的全部权重）。根据Amdahl定律，权重更新可能是训练性能的一项重大开销，并限制了权重较大（比如语言模型）或每副本上批量较小（大规模训练）模型的可扩展性。

因此，人们自然就想到把权重更新计算分片到多个副本上，但是简单的对权重更新进行切分可能会使副本之间的数据格式设置时间和通信开销显著增加。

首先，在具有平铺内存布局（ tiled memory layouts ）的现代加速器（modern accelerators）上，有效地划分张量是非常重要的。其次，由于前向和后向传播已经在副本中沿批次维度进行了划分，因此它们必须在下一个训练步骤中获得全部权重。除了高效通信原语的通用挑战外，另一个复杂问题是当今的优化器通常对于每个权重变量还需要几个辅助变量，如移动平均值（moving average ）和动量（momentum），每个辅助变量的大小与权重本身相同。这些辅助变量也需要随权重一起更新。

在权值更新没有分片的情况下，副本之间只需要传递梯度信息；使用权重更新分片之后，副本则需要传递权重和辅助变量，因此减少此开销至关重要。

多维权重张量的分片方式以及训练集群拓扑结构会给通信原语的效率带来高度影响。我们的图变换会仔细地为每个张量选择分片格式，以便有效地分片和取消分片。我们对于小规模和大规模训练使用不同的分片策略：对于小规模训练，我们优先考虑减小分片大小，因为副本的数量很小；对于大规模培训，我们将优先考虑减少通信延迟。

我们在TensorFlow中用XLA实现了这种分片方法，其中大部分的分析和转换通过XLA完成。

0x02 XLA背景知识

XLA（加速线性代数）是一种针对特定领域的线性代数编译器，能够加快 TensorFlow 模型的运行速度并改进内存用量。XLA 提供了一种运行模型的替代模式：它会将 TensorFlow 图编译成一系列专门为给定模型生成的计算内核。由于这些内核是模型特有的，因此它们可以利用模型专属信息进行优化。

2.1 All-reduce.

All reduce具有MPI All-reduce的语义，MPI All-reduce基于提供的二进制规约计算在参与设备之间规约张量。所有reduce都可以选择性地获取子组信息，因此reduce可以仅应用于设备的每个子组中。例如，{{0, 1, 2, 3} , {5, 6, 7, 8}}的子群分别合并设备0-3和设备4-7之间的值。

2.2 算子融合

融合操作符表示一组操作符，这些操作符可以作为计算单元由目标设备的后端发出。融合优化通过对可融合的算子进行分组，并将其替换为带有融合子计算（sub-computation）的融合算子。通常，这意味着融合运算符的中间结果被存储在寄存器或scratchpad memory之中，而无需将数据在全局存储器之间移动，这样可以节省存储器带宽。图1显示了融合为单个运算符的多个元素运算符的示例。

更高级的融合运算符使用方法是后端编译器在融合子计算中对运算符进行模式匹配，并生成语义上与原始实现等效的自定义实现。用于权重更新分片优化（reduce-scatter 和 all-gather融合）的融合操作符就对应于此用例。

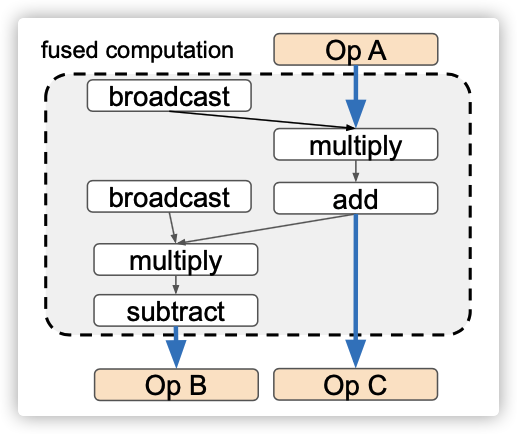
图1：具有元素级别操作（element-wise）的融合操作。蓝色粗箭头表示从全局存储器到全局存储器的数据传输，所有中间结果都存储在本地存储器中。

0x03 权重更新分片

图2 具有两个副本的同步数据并行

图2显示了典型的数据并行场景，其具有两个副本，是同步训练。在每个训练步骤中，每个副本使用训练输入批次中自己对应的分区来计算其局部梯度，然后所有副本使用all-reduce操作符来获得总梯度。在训练步骤结束时，所有副本对其权重副本应用相同的总梯度（summed gradients）。只要它们从相同的初始权重开始，这就可确保它们始终保持权重同步。

对于具有较大权重的模型，如Transformer等语言模型，训练步骤会花费大量时间来更新权重。对于像ResNet这样的图像模型，虽然权重通常较小，但当它们在具有许多设备的大规模设置中进行训练时，每个core对应的批次通常被设置为较小的值，以避免过大的全局批（global batch size）大小，这使得权重更新也相对费时费力。

权重更新是受到内存限制的：计算大多是简单的元素级别操作，但对于每个权重变量，它需要读取梯度、原始权重和辅助变量，然后写回更新的权重和更新的辅助变量。

通常，因为权重和梯度没有要分区的批次维度，所以权重更新不会在数据并行性中分片。本论文的目标是：在不使用更多设备的情况下，在副本设备上实现分块权重更新，达到优化的目的。

3.1 All-reduce分解

原文小标题为 Sharding with decomposed all-reduce。

一个典型的all-reduce实现一般分为两个阶段：reduce-scatter和all-gather。在reduce-scatter阶段，副本在不同的数据分片上分几轮交换数据，最后，每个副本都有一个来自所有副本的完全规约的数据分片。在“all-gather”阶段，副本执行新的交换，以向所有其他副本广播它们自己的完全规约的分片。

如下图所示，我们可以使用reduce scatter生成每个副本分片的求和梯度，就是图中的 gradient shard，这样每个副本都可以在分片上执行权重更新。之后，我们可以使用all gather向所有副本广播更新的权重分片。“reduce-scatter”和“all-gather”的组合应该具有与原始“all-reduce”类似的性能。但是因为每个副本会自己更新权重分片（update weight shard），所以总的耗时会降低，这样就相当于总的权重更新被各个副本均匀分担了。

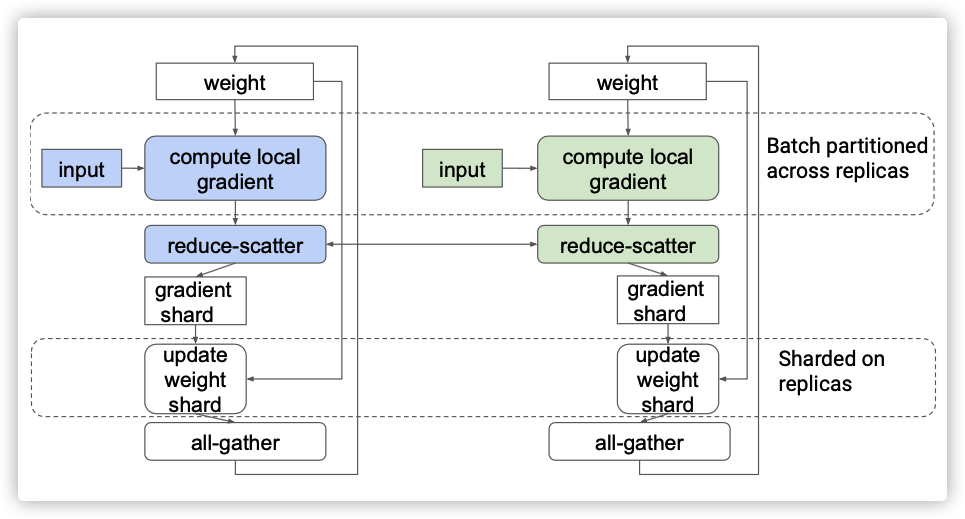
图3，使用 “reduce-scatter”和“all-gather” 组合的分片方案

一个复杂问题是在优化器中如何处理辅助变量。我们知道，优化器通常包含其他参数，例如，对于每个权重，Adam优化器需要维护两个变量：梯度的"平方和（squared gradients）"以及"指数移动平均值（exponential moving averages）"。这些变量是训练状态的一部分，其包含在模型检查点中，因此通常更新的值也是训练步骤输出的一部分。如果我们在每个训练步骤结束时都对每个辅助变量进行 all-gather，那么通信开销将太大。然而，这些变量仅在权重更新时由优化器使用，而在计算梯度的向前和向后过程中不需要。因此，一个优化的解决方案可以在迭代中保持辅助变量的分片，直到检查点或汇总阶段才进行all-gather。

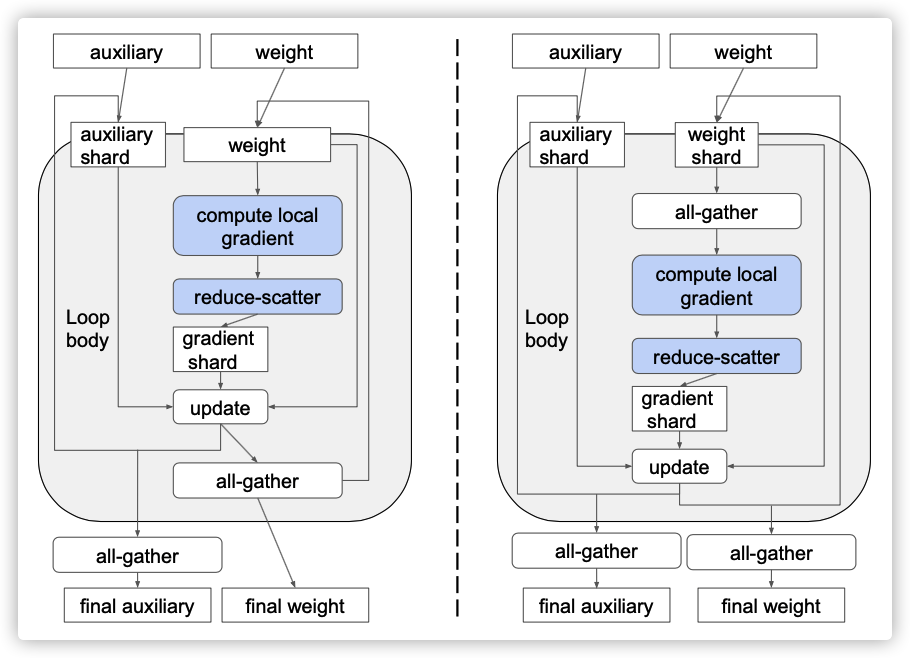
图4：使用循环来切分辅助变量的两种方法。左图：仅在迭代中保持辅助切分。右图：在迭代过程中保持辅助变量和权重分片，并在向前/向后传递之前收集所有权重。

• 编译器可见循环。如果编译器（graph Optimization）可以在计算图中发现一个训练循环，那么它可以在循环之后执行辅助变量的 all-gather，从而分摊成本。如果没有发现循环，它则需要运行时系统的额外帮助。

• 辅助变量的其他用途。虽然辅助变量仅在权重更新时用到，但现实的模型通常包括一些自定义逻辑，例如获取当前训练进度的摘要，该摘要可能使用变量的完整状态。这样的操作可能位于训练循环体内部，但通常因为保护机制，这样的操作只在每k步才发生一次。

左图和右图的区分是：循环内权重的all-gather位置不同，左图是在update之后立即做weight all-gather，右图是计算梯度之前做weight all-gather，并且在跳出循环之后还要做一次all-gather。

左图方法似乎对性能更有利，因为它不需要在循环后对权重进行all-gather，即使这应该只是一个很小的摊余成本。然而，我们在实践中发现，第二种方法通常支持更高级的优化。主要区别在于，在第二种方法中，权重更新不再依赖于完整权重。权重更新只需要步骤开始时提供的那些分片数据，向前和向后传播才需要all-gather之后的完整数据。在许多图像和语言模型中，向前和向后传播使用权重作为卷积或矩阵乘法的输入，而卷积或矩阵乘法通常对其输入具有较低的精度要求。例如，在使用Cloud TPU的典型训练中，卷积输入的精度可以被降低到bfloat16，而权重更新通常才需要float32。使用第二种方法，可以在bfloat16中执行全权重的all-gather，如图7所示，这大大减少了内存访问和通信量。这种精度优化是通过基于数据流的精度传播过程自动完成的。

后文还会继续分析。

3.2 挑战

接下来，我们看看几个关键的挑战。

• 分片格式。在具有平铺内存布局（tiled memory layouts）的加速器上，如何将张量在不同副本之间划分是很棘手的，因为格式化数据可能会很费事费力。此外，张量上的单个维度可能会太小或无法在副本之间均匀共享。为了使张量的切分有效，我们的系统选择了一组廉价的重新格式化步骤，这些步骤可以有效地融合到切分/取消切分操作之中。

• 非元素级别（Non-elementwise）优化器。对于某些优化器，权重更新计算可能包括非元素级别操作。例如，一些优化器使用权重范数或均方根，这涉及到reduce运算符。我们将讨论如何在分片数据上运行非元素级别计算的解决方案。

• 大型拓扑中的通信。当副本数量较大时，张量的分片可能非常小，因此reduce-scatter和all-gather 将成为延迟限制（ latency-bound）。在这种情况下，我们的系统将选择在副本的子组（subgroups）之间部分地分配权重更新计算，并使用批通信操作来减少大型网络拓扑上的延迟。

0x04 图转换

4.1 分片表示

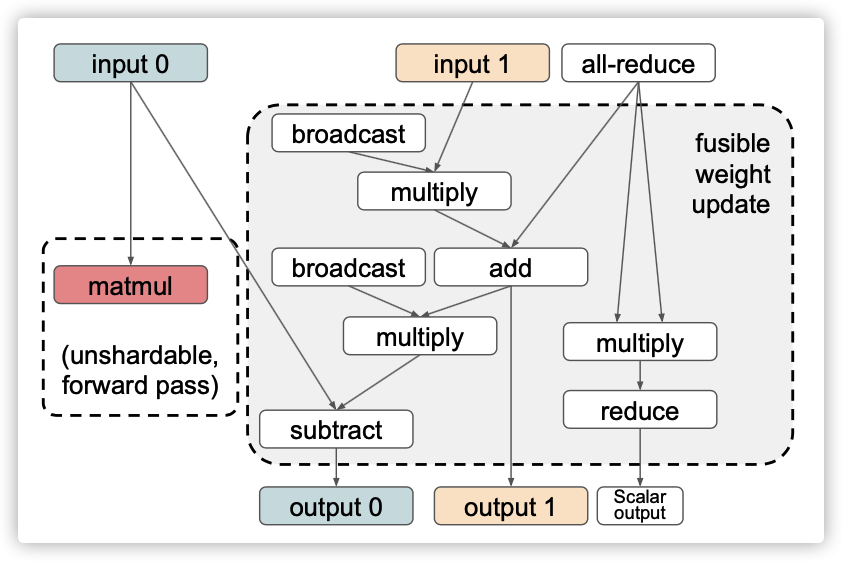
图5: all-reduce相关的权重更新操作符。如果这是在一个循环中，那么输入1和输出1可以在迭代之间分片，并且输入0和输出0（在输出0之前或matmul之前）之间只需要一个all-gather集合。

对于一组权重更新操作符（图5），所有输入（梯度、原始权重和辅助变量）必须以相同的方式进行切分，因为它们在权重更新期间被同一组元素级操作符使用。在没有权重更新分片的情况下，虽然all-reduce也实现为 reduce-scatter阶段和all-gather阶段，因为分片不需要暴露给其他操作符，所以它可以在内部选择任意分片。相反，使用分片权重更新时，通信原语使用的分片格式必须与输入上的分片相匹配。

权重张量表示为多维数组。在像 Cloud TPUs这样具有分片内存布局（tiled memory layouts）的处理器中，拆分某些维度可能比拆分其他维度更昂贵。所选分片还必须由reduce-scatter和all-gather操作符支持。因此，我们总是选择一个对于切分是有效的，并且更容易在reduce-scatter和all-gather中得到支持的维度。

4.1.1 数据格式化

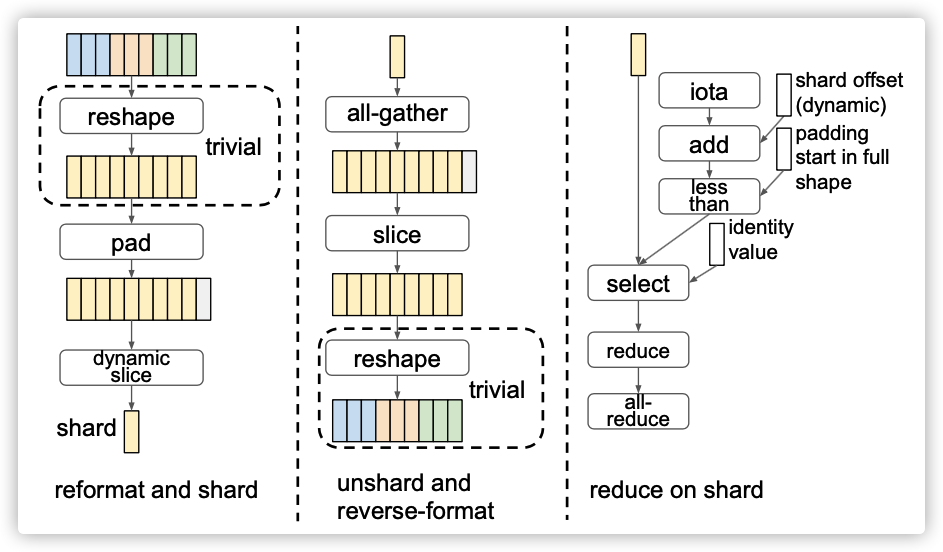
Figure 6: Sharding and unsharding with reformatting.

右图显示了通过重新格式化进而在分片上处理非元素级别运算符的示例。

一个常见的问题是，所希望的分片维度不能被分片（副本）的数量平均整除。例如，ResNet具有形状为[3,3,256,256]的权重，其中[3,3]是所需的分片维度，但分片计数也许是8。为了解决这些问题，我们允许在对副本进行分片之前重新格式化张量。因此，张量的分片被表示为一系列数据格式化操作符，然后跟着一个动态切片（dynamic-slice）操作符，如图6所示。动态切片指定分片的维度，并使用副本id为每个副本计算分片的偏移量。

格式化操作符可以包括组合维度的重塑（reshapes）操作，以及使维度可被分片总数切分的填充操作。维度组合通常在填充之前进行，这有助于最小化填充数目。例如，[3,3,256,256]可以重新整形为[9,256,256]，这允许在副本总数为10时将其填充到[10,256,256]，而不是填充到[10,3,256,256或[4,5,256,256]。

还有另一个平台相关的重新格式化操作符 bitcast。这意味着只要新形状在设备上没有超出范围，就可以将设备内存重新解释为一个不同的形状。

此外，我们只选择那些可以有效地融合（fuse）到周围运算符的重新格式化运算符。例如，pad操作符应该融合到动态切片（dynamic-slice）中，这样它就不会访问完整形状的整个内存缓冲区。

4.1.2 Non-elementwise 算子

虽然权重更新中的大多数操作符都是简单的元素级别算术操作符，但一些优化器也包括非元素级别操作符，最常见的是reduce。

非元素运算符可能会限制如何对张量的重新格式化。在reduce操作符中会使用reduce函数折叠（collapse）某些维度，并将其他维度直接传递给最终结果；这样就不允许通过重塑（reshape）或bitcast将折叠维度与直传（pass-through）的维度组合在一起。由于所有维度都已折叠，因此这并不限制“reduce-to-scalar”操作符。

另一个限制是填充。折叠维度中的填充数据元素可能会影响reduce的结果，因此它们必须用标识值来屏蔽（mask），例如，0表示加法，1表示乘法。这要求填充数据的位置在重新格式化后必须是可识别的。如果填充源是作为一个明确的重新分组步骤引入的，而后面没有reshape或bitcast，则可以按照填充操作符中的规定来识别位置；相反，限制通常是针对bitcast中的隐式填充：平铺内存布局已经暗示了填充，重新解释内存缓冲区可能会丢失一些填充信息。因此，根据平台的张量内存布局，某些bitcast在支持reduce运算符时可能会带来复杂性。

如果分片影响了折叠的维度，则针对reduce操作符需要额外处理。首先，每个副本都需要屏蔽填充的数据。不同副本上的填充区域不同，这取决于其分片在完整shape中的位置，这要求掩码在同一训练计划中是动态的。如图6所示，这可以通过比较元素的位置(iota+ start offset) 和填充区域在整个shape上的位置来实现，然后根据比较结果在分片数据和标识值之间进行选择。其次，副本需要使用all-reduce来组合其reduce的结果。这是因为折叠的维度在reduce结果中已经丢失，因此它们无法分片，但每个副本的本地结果不同于其他副本，其仅从其自己的输入分片捕获数据。

4.2 训练计算图转换

如第3.2节所述，all-gather 操作符如何放置对性能至关重要。在训练循环的帮助下，我们通常只需要在循环内放置一个 all-gather。

4.2.1 循环外放置

原小标题为：Out-of-loop all-gather placement。

如果训练循环是编译器可见的，那么辅助变量的all-gather操作符可以放在循环之后，后面跟着所需的反向格式化操作符。相应地，在循环开始之前，需要使用重新格式化（reformatting）运算符和动态切片（dynamic-slice）对原始辅助变量值进行切分，如图6所示。

如果编译器没有发现循环，通过将辅助变量的切分和取消切分（sharding and unsharding）移到训练步骤程序之外，仍然可以从权重更新切分中获益。一种解决方案是在计算图转换之后生成三个单独的程序：切分程序、主程序和unsharding程序。切分程序包含训练循环前变量的切分算子；主程序包含训练步骤和分片权重更新；unsharding程序包含用于重建完整变量的all-gather操作符。运行时系统负责在正确的时间调用每个程序。例如，如果运行时系统管理训练循环，它可以在循环前后调用切分/unsharding程序；即使运行时没有看到循环结构，它仍然可以维护跟踪每个变量是否被切分，并在状态不匹配时有条件地调用切分/取消切分程序。

In-loop all-gather placemnt

在图4中，我们展示了两种可能的方式来放置all-gather，以便向前和向后传播可以使用权重。左图显示了一种显式方式，即all-gather都位于训练步骤的末尾，这样权重在下一次迭代开始时已经处于完整状态。相反，右图会在循环迭代中保持权重分片，就像对于辅助变量一样，但会在向前和向后过程需要之前执行所有聚集。

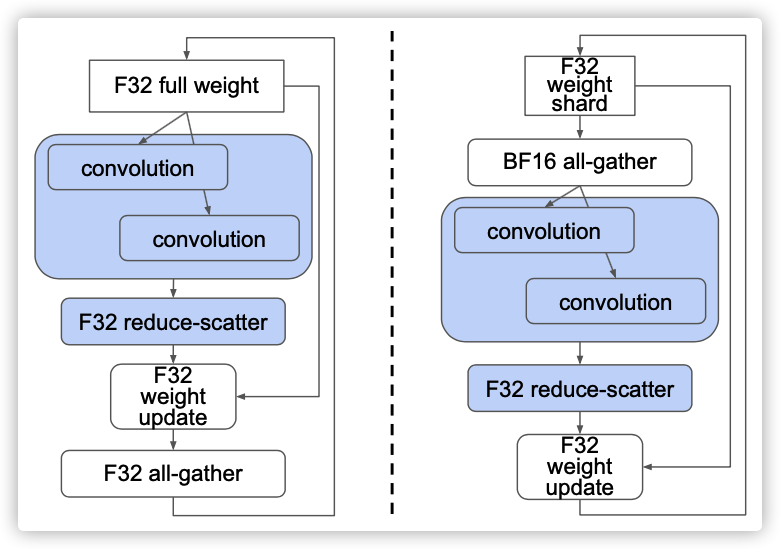
图7：通过在迭代中保持权重分段（右图），只需要在bfloat16精度中使用完整权重。

第一种方法似乎对性能更有利，因为它不需要在循环后对权重进行all-gather，即使这应该只是一个很小的摊余成本。然而，我们在实践中发现，第二种方法通常支持更高级的优化。主要区别在于，在第二种方法中，权重更新不再依赖于完整权重。权重更新只需要步骤开始时提供的那些分片数据，向前和向后传播才需要all-gather之后的完整数据。在许多图像和语言模型中，向前和向后传播使用权重作为卷积或矩阵乘法的输入，而卷积或矩阵乘法通常对其输入具有较低的精度要求。例如，在使用Cloud TPU的典型训练中，卷积输入的精度可以被降低到bfloat16，而权重更新通常才需要float32。使用第二种方法，可以在bfloat16中执行全权重的all-gather，如图7所示，这大大减少了内存访问和通信量。这种精度优化是通过基于数据流的精度传播过程自动完成的。

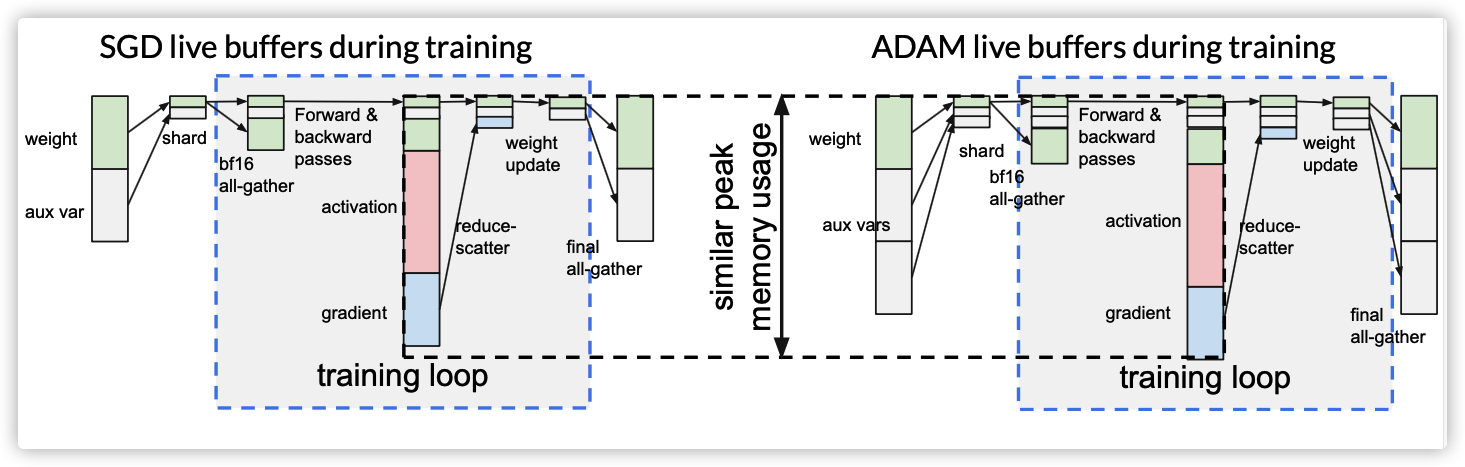
4.2.2 内存节省

通过上述转换，权重和辅助变量的生存范围得到了缩小。特别是对于辅助变量，只需要在训练循环之外使用其完整数据缓存区。因此，可以重用它们的缓冲区来存储向前和向后过程中的激活和梯度。如图8所示，这允许具有不同大小辅助变量的优化器们具有相似的峰值内存使用率。

更准确地说，假设权重的总大小为W，辅助变量的总大小为V（优化器特定），向前和向后传播过程中实时激活和梯度的峰值大小为P，那么我们可以在技术上将峰值内存使用从W+V+P减少到 max(W +V/N +P,W +V)。其中N是分片数。这使得ADAM优化器在性能和内存方面与SGD一样高效。

0x05 高效通信

即使理论上，reduce-scatter和all-gather 组合的通信量与无权重更新分片的 all-reduce相当，reduce-scatter和all-gather的高效实现对性能也非常重要。这有两个挑战，匹配张量上指定的分片表示（第4.1节）和避免小分片上的延迟限制通信。

5.1 数据融合

原小标题为：Fusion with data formatting。

我们需要为分片中的每个张量选择格式化步骤，以确定如何将其划分为分片。如果我们在reduce-scatter之前填充梯度，则需要每个副本对完整数据执行本地读写。为了避免这种低效，我们将格式化操作符融合到reduce scatter和all gather中。通过这种融合方法，我们可以在不需要在算子上引入复杂的配置的情况下表达灵活的切分；事实上，我们甚至不需要定义专用的reduce-scatter或all-gather操作符，因为它们可以使用all-reduce表示，如图9所示。

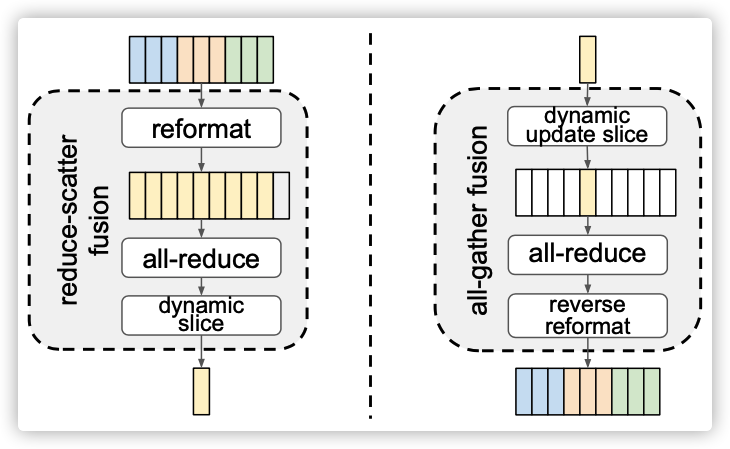
图9：用重新格式化和all-reduce融合的方法来减少reduce-scatter和all-gather。

在一个N副本上使用reduce-scatter和all-gather 的经典算法中，数据被划分为N个片段，副本形成一个逻辑环，并与邻居在多轮中交换片段。在我们的融合实现中，这些片段的边界必须与切分格式完全匹配，并且在准备数据片段时完成填充操作。

融合操作符的实现还保证分配给副本的分片与它在逻辑环中的位置相匹配，因此经典算法最终将在每个副本上生成所需的分片。由于如何利用物理网络链路的带宽对逻辑环至关重要，因此我们根据网络拓扑选择分片ID，而不是相反。实际上，为了利用特定的网络拓扑结构，可以在多个阶段实现reduce-scatter和all-gather。例如，对于设备的N×M阵列进行大小为D的reduce-scatter，我们可以转换为：先对每一行进行D/M为分片大小的reduce-scatter操作，然后对每一列进行D/(MN)为大小的reduce-scatter操作。在这种情况下，需要根据所有阶段的拓扑结构来计算分片ID。

5.2 利用网络带宽

原小标题是Utilizing network bandwidth for large topology。

在副本数量较大的大规模训练中，权重或梯度张量的分片大小可能非常小。例如，一个Cloud TPUv3有2048个核（两个核共享一个芯片），因此如果一个4 MB张量以2048种方式分区，分片大小将只有2 KB。首先，一个明显的问题是通信很容易受到延迟限制；其次，小分片本身可能需要在平铺内存布局中进行大量填充，因此实际传输的数据大小可能比完整张量大得多。

5.2.1 部分分片（Partial sharding）

实际上，与64路的切分相比，2048路的切分权重更新并不能提供可观的节省空间，因为与训练步骤的其余部分相比，切分权重更新时间已经很短。因此，我们可以选择将副本组织成独立的组，每个组执行自己的分片。然而，每组reduce-scatter仅产生部分结果，因为它不会累积来自其他组的数据。因此，在reduce-scatter后，需要跨组进行all-reduce。

对于N×M副本阵列，可以将分片组定义为N行，并且将在每个M列上执行 all-reduce（图10）。通信可能仍将受到延迟限制，因为all reduce发生在reduce-scatter的已分片输出上，因此all reduce的内部分片大小仍然是D/(MN).。事实上，正如我们接下来所展示的，分组有助于实现更积极的小数据传输批处理。

Figure 10: Partial sharding and batched communication.

5.2.2 批量处理通信算子(Batched communication operators)

不同权重变量的更新计算通常相互独立，因此我们可以将它们的通信运算符组合在一起。因为它们共享由网络拓扑确定的组以及相同的分片机制，所以这是可能的。

组合的“ reduce-scatter”或“all-gather”必须为每个张量维持其原始分片分配机制。为了实现这一点，每个组合分片由来自每个张量的一个分片组成。如果在一个张量的分片上有过多的填充，它很可能保留在组合分片中。此外，在多阶段reduce-scatter和 all-gather中，如何跟踪这些分片边界也是一项挑战。

相比之下，组合的all reduce不需要考虑单个输入张量的任何切分，因为其内部切分不需要公开。这使得更加容易处理和高效的在组合小张量上实现all-reduce。输入张量可以在概念上以完整的形状连接在一起，内部分片是连接形状上的分区，如图10所示。除了子组reduce分散后的all reduce之外，图6中部分标量reduce结果的all reduce还可以与其他类似的all reduce操作符组合。

因此，部分分片（partial sharding）将小分片的大部分处理工作延迟到组合的all reduce运算符中，其中reduce-scatter和all gather仅在单个阶段执行组合运算符。这在很大程度上避免了小分片的延迟限制通信。小型通信运算符的批处理由编译器过程自动完成。

至此，两篇论文介绍完毕，下一篇开始进行代码解析。

0xFF 参考

https://tensorflow.google.cn/xla?hl=zh-cn

Fully Sharded Data Parallel: faster AI training with fewer GPUs

https://github.com/microsoft/DeepSpeed

ZeRO: Memory Optimizations Toward Training Trillion Parameter Models

Automatic Cross-Replica Sharding of Weight Update in Data-Parallel Training