【reverse】逆向1 数据宽度

前言

感觉学逆向的都是大佬，正好最近在看java视频的时候，发现讲课的老师居然是从逆向行业转行来的，顿时肃然起敬。于是想在暑假的最后发光发热，把逆向的基础知识学习稳固一下！

学习是跟着b站的滴水逆向学习的

1、前置知识

数学上的数字是没有大小限制的，可以无限大
但是计算机中，受到硬件的制约，数据都是有长度的
计算机中有很多容器，这些容器来装数据
如果容器存不下，计算机直接扔掉

4位宽度

4位宽度表示：假设计算机只能存储4位2进制数

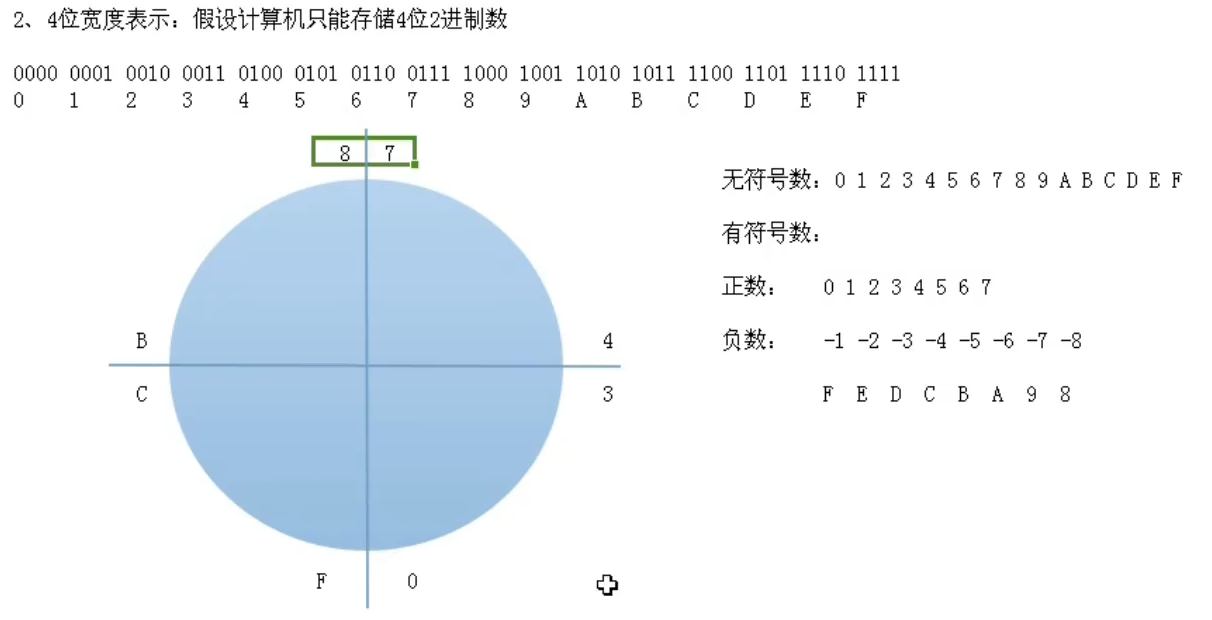
按照这张图，如果我们规定计数是无符号数，那么，从0到F，可算16个数据，并且，如果F上还要加1，那么数据直接溢出为0

如果我们计数是有符号数，分为正数和负数

但是计算机存的就只有16个数据，所以正负分一半，各8个，所以0、1、2、3、4、5、6、7右半部分，我们规定是正数，F、E、D、C、B、A、9、8，左半部分我们规定是负数。

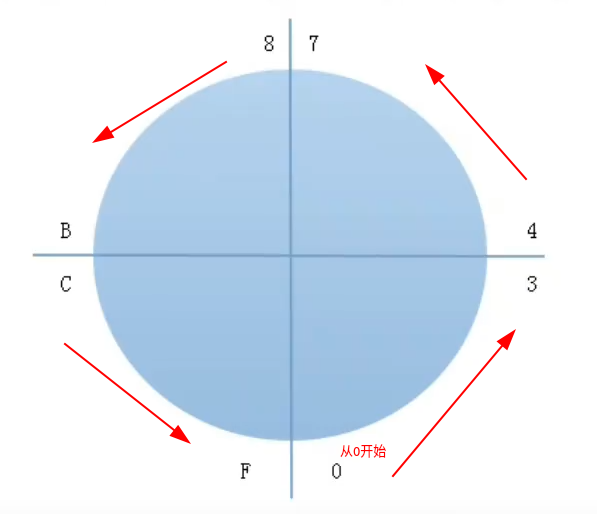
并且F是最大的负数（-1），因为F加上任意正数，都是向右转。

如果只看二进制的话，并且分正负数，我们发现四位二进制，如果是0开头的都是正数，如果是1开头的都是负数

所以是我们人来定义正负、有无符号，计算机十分单纯，只能用01来表示

8位宽度

8位宽度表示：假设计算机只能存储8位2进制数

无符号数： 0 ～ FF（255）

有符号数：

正数：0 ～ 7F （127）
负数：FF ～ F4 （-1 ～ -128）

只有我们把数看作有符号数，第一位数是1才是负数

16位宽度

16位宽度表示：假设计算机只能存储16位2进制数

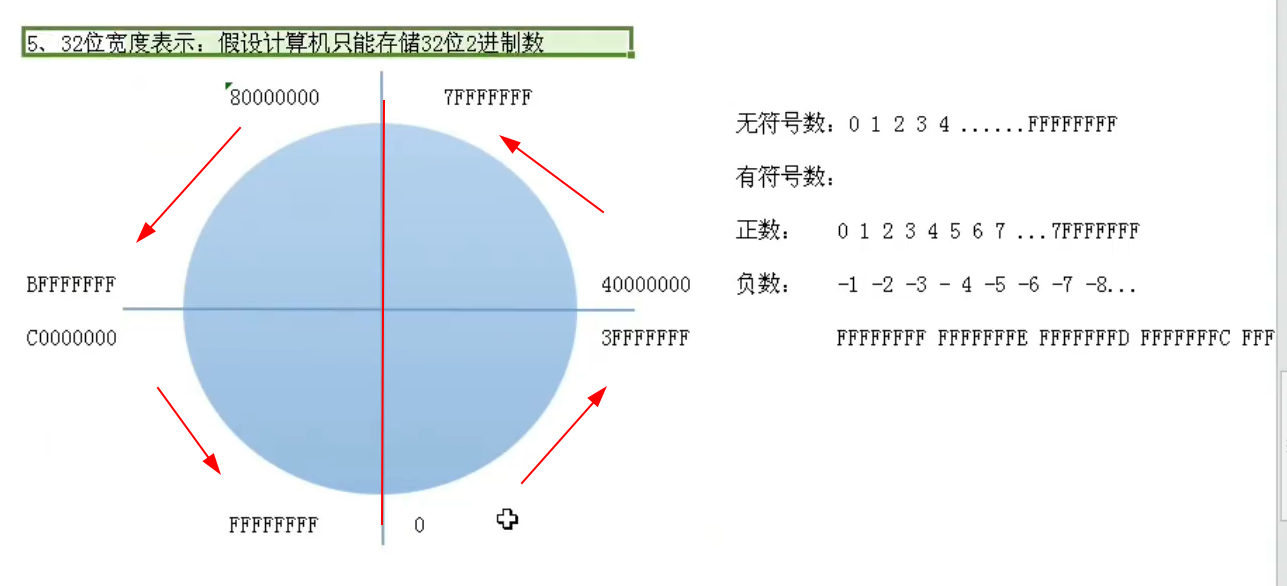
32位宽度

32位宽度表示：假设计算机只能存储32位2进制数

几个重要的计量单位

BYRE 字节 8BIT

WORD 字 16BIT 2字节

DWORD 双字 32BIT 4字节

2、二进制的逻辑运算

数字电路都学过：

三种基本逻辑运算：与或非

然后还有比较重要的一个异或

与： and &

或： or |

非： not !

异或： xor ^

逻辑运算的具体应用

1、CPU如何计算4+5=？

4+5

# 4+5计算机是如何操作的？

# 我们人进行二进制计算

0000 0100

0000 0101

---------（我们使用加法，但是计算机不会）

0000 1001

# 计算机进行计算

# 1、异或（相当于不进为的加法）

0000 0100

0000 0101

---------

0000 0001

# 2、与运算（判断进位）

0000 0100

0000 0101

---------

0000 0100

# 3、与运算结果左移一位

0000 0100

---------

0000 1000

# 4、将1和3步骤异或，得到加法正确结果

0000 0001

0000 1000

---------

0000 1001

# 5、与运算（计算机验证是否结果为0）

0000 0001

0000 1000

---------

0000 0000

# 所以最终的结果就是与运算为0的结果的上一个异或运算

4-5

# 计算机没有减法，4-5 = 4 + （-5）

# 计算机中负数使用补码

0000 0100

1111 1011

---------

1111 1111

# 1、异或

0000 0100

1111 1011

---------

1111 1111

# 2、与运算

0000 0100

1111 1011

---------

0000 0000

# 因为与运算结果为0，我们取上一次异或的结果

4x5

本质就是4个5相加

4/5

本质就是算4能减去几个5（加上几个-5）

2、如果想获取某个值的第N位是多少？

如：8F的第3位是什么？

	1000 1111

and 0000 0100

-------------

	0000 0100

# 通过与第N位相与一个1，来看这一位是多少

# 得到的结果是0，那么测试的这一位就是0，非0就是1

3、最简单的加密算法

3、总结

了解计算机如何存储数据
了解数据宽度
了解正负数、无符号数的本质
掌握逻辑运算，并了解计算的本质

4、课后作业

1、为什么八进制数2-5在计算器中的结果是1 777 777 777 777 777 777 775？

我们看8位宽度的图

2-5肯定是个负数，以中间为分界线，FF是最小的负数（-1）

2减去一个5，就是逆时针转动5个单位，转到了FD

FD是-3，所以在计算器中，八进制2-5，16进制得到的是FFFF FFFF FFFF FFFD