欧拉函数&筛法 模板

https://blog.csdn.net/Lytning/article/details/24432651

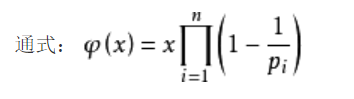   记牢通式

=x((p1-1)/p1) * ((p2-1)/p2)....((pn-1)/pn)

求一个整数的欧拉函数：

int eular(int n){
    int res = n, x = n;
    for(int i = 2; i*i <= x; i++){
        if(x % i == 0){ //是其中的一个质因数
            res = res/i*(i-1);//保证为整数 且不会溢出
            while(x%i == 0) x /= i;
        }
    }
    if(x > 1) res = res/x*(x-1); //可能是最后一个质数
    return res;
} 

求[1, n] 之间的数的欧拉函数  筛法：

首先：

性质 1. phi(p)=p-1   因为质数p除了1以外的因数只有p，故1至p的整数只有p与p不互质

性质 2. 如果i mod p = 0, 那么phi(i * p)=p * phi(i)

性质 3. 若i mod p ≠0,  那么phi(i * p)=phi(i) * (p-1)

// 和素数的欧拉筛法
void get_eular(int n){
    int visti[MAX_SIZE];
    int s[MAXN_SIZE], tot = 0;
    int phi[MAX_SIZE];
    memset(visit, 0, sizeof visit); //visit[i] = 0 表示 i 为素数
    for(int i = 2; i <= n; i++){
        if(!visit[i]){
            phi[i] = i - 1;  //性质1
            s[tot++] = i;
        }
        for(int j = 0; j < tot; j++){
            if(i*s[j] > n) break; //这个不能忘
            visit[i*s[j]] = 1;
            if(i % s[j] == 0){
                phi[i*s[j]] = phi[i] * s[j]; //性质2
                break;
            }else{
                phi[i*s[j]] = phi[i] * (s[j] - 1); //性质3
            }
        }
    }
}