浅淡fhq_Treap

浅淡 \(fhq\_Treap\)

前言

fhq_Treap \(yyds\)!

\(sto\ FHQ\ orz\)

机房大佬们都打的 \(Splay\) 只有蒟蒻打的 \(fhq\) （防火墙）（范浩强）_\(Treap\) QAQ!

\(fhq\) 代码短，好理解，操作少，常数小，可区间，可持久化，\(Splay\) 行的它都行（先不说LCT ），\(Splay\) 不行的它也行，除了不能旋，哪里不如 \(Slpay\) ？ 那为什么不学一手呢？

---

引入

正常的平衡树，像 \(Treap\) ，\(Splay\) 这样的，维持平衡的主要操作都是靠旋转。

通过不断将节点想上层旋转，以满足二叉树的性质的同时，使另一值保持堆的性质，以达到维持二叉树平衡（不让其退化成一条链）的目的。

这样虽然可以平衡二叉树，但不利于可持续化。

因为你每一次旋转都会破环树的形态（几乎完全改变），难以维护历史版本。

于是，神犇 \(FHQ\) 便发明了不用旋转的平衡树 —— \(fhq\_Treap\)。

---

基操

先把一些基本的东西给出来。

以下的 ”值“ 都是指平衡树维护的值（一般题目给出的或求出的 \(dp\) 值）；以下的 ”标志“ 都是指随机 \(rand()\) 给点的值。

这是一棵平衡树

struct Treap
{
	int val,rand,ls,rs,size;
    	//分别指：“值”，“标志”，左儿子，右儿子，子树大小
}tr[N];

新建一个节点

inline int New(int val)
{
	tr[++num]={val,rand(),0,0,1};
	return num;//返回节点编号
}

更新（\(pushup\)）

inline void Update(int x)
{
	tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}

不用旋转，\(fhq\_Treap\) 靠两种操作解决一切问题。

分裂（Split）

将一棵平衡树以某个值（\(val\)）为界，分成两棵平衡树，一棵树上的节点的值全部小于等于 \(val\) ，另一棵树的则全部大于 \(val\) 。

inline void Split(int p,int val,int &x,int &y)
//当前在 p 节点，以 val 为界，划分出分别以 x,y 为根的两棵平衡树
{
	if(!p) return (void)(x=y=0);//搜到空节点，返回空节点
	if(tr[p].val<=val)//当前值小于 val ，界线在右边，向右划分
	{
    	x=p;//更新较小树的根
		Split(tr[p].rs,val,tr[p].rs,y);
	}
	else//同理
	{
		y=p;
		Split(tr[p].ls,val,x,tr[p].ls);
	}
	Update(p);//由于分裂完后左右儿子可能会变，所以要更新一下节点信息
}

时间复杂度：\(\Theta(logn)\)

合并（Merge）

将两棵一大一小（一棵的值全部大于另一棵的值，即值域无交集）的平衡树树合并成一棵平衡树，并满足平衡树的性质：值为二叉树，标志为堆。

inline int Merge(int x,int y)//x为较小树的根，y为较大树的根 ,返回合并后树的根
{
	if(!x||!y) return x+y;
	if(tr[x].rand<tr[y].rand)//满足堆的性质
	{//因为x的值比y小，而x又必须在y的上面，所以根据二叉树性质，y只能在x右子树中
		tr[x].rs=Merge(tr[x].rs,y);//让y继续合并
		Update(x);
		return x;
	}
	else
	{//因为x的值比y小，而y又必须在x的上面，所以根据二叉树性质，x只能在y左子树中
		tr[y].ls=Merge(x,tr[y].ls);
		Update(y);
		return y;
	}
}

注意：由 \(Merge(x,y)\) 中的\(x\) 与 \(y\) 的树的值之间有大小关系，故不能随意交换 \(x\) , \(y\) 的顺序写成 \(Merge(y,x)\) 。

时间复杂度：\(\Theta(logn)\)

---

有了这两个，直接上题

P3369 【模板】普通平衡树

1.插入（Insert）

我们可以把要插入的值直接调用 \(New()\) 弄成一个点，再把它看作一颗只含根的树与原平衡树合并。

但合并具有大小关系的限制，所以我们先把原树裂成以这个值为界的两棵树，再进行两次合并。

inline void Insert(int val)
{
	int x,y;
	Split(rt,val,x,y);
	rt=Merge(Merge(x,New(val)),y);//注意这里Merge里两根的位置
}

2.删除（Delete）

删除就是插入反着来。

先把树分成三棵，把要删的孤立出来，再把要删节点的左右儿子合并成一棵树代替它，最后把三棵树合并起来。

inline void Delete(int val)
{
	int x,y,z;
	Split(rt,val,x,z);Split(x,val-1,x,y);
	y=Merge(tr[y].ls,tr[y].rs);
	rt=Merge(Merge(x,y),z);
}

3.查询值的排名（Rank）

到这里我们之前 \(Update()\) 维护的 \(size\) 便排上用场了。

还是按给定的值把树裂成两棵，这样比这个值小（严格小于）的都分到一棵树里去了，那么这个值的排名就是这棵树的大小+1。

inline int Rank(int val)
{
	int x,y;
	Split(rt,val-1,x,y);
//不能以val为界，因为我们要求的是严格小于val的树，当然这取决于你Split中是“<”还是“<=”
	rt=Merge(x,y);
	return tr[x].size+1;
}

4.查询排名的值（Find）

这个你甚至都不需要分裂或是合并。

inline int Find(int p,int Kth)//在以p为根的树中找排名为Kth的值（从小到大排）
{
	if(Kth==tr[tr[p].ls].size+1) return p;//这个很显然吧。。。
	if(Kth<=tr[tr[p].ls].size) return Find(tr[p].ls,Kth);//往左子树找
	return Find(tr[p].rs,Kth-tr[tr[p].ls].size-1);//往右子树找
}

5.前驱

很容易想到，把比给定值严格小的树裂出来，这棵树中最大的就是这个值的前驱。

inline int Pre(int val)
{
	int x,y;
	Split(rt,val-1,x,y);
	if(!x) return -inf;//没有前驱（有些题会考）
	int ans_p=Find(x,tr[x].size);
	rt=Merge(x,y);
	return tr[ans_p].val;
}

6.后继

后继和前驱思路基本一致，把比给定值严格大的树裂出来，这棵树中最小的就是这个值的后继。

inline int Next(int val)
{
	int x,y,anss;
	Split(rt,val,x,y);
	if(!y) return inf;//没有后继
	int ans_p=Find(y,1);
	rt=Merge(x,y);
	return tr[ans_p].val;
}

然后就完了。

最后奉上完整代码。

#include <bits/stdc++.h>
#define re register
//#define int long long
#define lss tr[p].ls
#define rss tr[p].rs
#define END system("pause")
#define inf 0x7fffffff
using namespace std;
inline int read()
{
	re int x=0,f=1;
	re char c=getchar();
	while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+c-48;c=getchar();}
	return x*f;
}
const int N=1e5+5;
int rt,num;
struct Treap{int val,rand,ls,rs,size;}tr[N];
inline int New(int val){tr[++num]={val,rand(),0,0,1};return num;}
inline void Update(int p){tr[p].size=tr[lss].size+tr[rss].size+1;}
inline void Split(int p,int val,int &x,int &y)
{
	if(!p) return (void)(x=y=0);
	if(tr[p].val<=val){x=p;Split(rss,val,rss,y);}
	else{y=p;Split(lss,val,x,lss);}
	Update(p);
}
inline int Merge(int x,int y)
{
	if(!x||!y) return x+y;
	if(tr[x].rand<tr[y].rand){tr[x].rs=Merge(tr[x].rs,y);return Update(x),x;}
	tr[y].ls=Merge(x,tr[y].ls);return Update(y),y;
}
inline void Insert(int val)
{
	int x,y;Split(rt,val-1,x,y);
	rt=Merge(Merge(x,New(val)),y);
}
inline void Delete(int val)
{
	int x,y,z;Split(rt,val,x,z);Split(x,val-1,x,y);
	rt=Merge(Merge(x,Merge(tr[y].ls,tr[y].rs)),z);
}
inline int Rank(int val)
{
	int x,y,anss;Split(rt,val-1,x,y);
	anss=tr[x].size+1;rt=Merge(x,y);
	return anss;
}
inline int Find(int p,int Kth)
{
	if(tr[lss].size+1==Kth) return p;
	if(Kth<=tr[lss].size) return Find(lss,Kth);
	return Find(rss,Kth-tr[lss].size-1);
}
inline int Pre(int val)
{
	int x,y,anss;Split(rt,val-1,x,y);
	anss=tr[Find(x,tr[x].size)].val;rt=Merge(x,y);
	return anss;
}
inline int Next(int val)
{
	int x,y,anss;Split(rt,val,x,y);
	anss=tr[Find(y,1)].val;rt=Merge(x,y);
	return anss;
}
signed main()
{
	srand(998244353);
	int T=read();
	while(T--)
	{
		int op=read(),val=read();
		if(op==1) Insert(val);
		else if(op==2) Delete(val);
		else if(op==3) printf("%d\n",Rank(val));
		else if(op==4) printf("%d\n",tr[Find(rt,val)].val);
		else if(op==5) printf("%d\n",Pre(val));
		else printf("%d\n",Next(val));
	}
	return 0;
}

在人性压行下 \(fhq\) 主体部分也就 \(50\) 行，总代码 \(2kb\) 左右，跑得还贼快。

---

区间

然后我们迎来了区间问题。

这类问题一般都是用平衡树维护序列下标。

对于区间操作，我们只需将要操作的那段区间用 \(Split()\) 出来，然后操作，然后再 \(Merge()\) 回去。

大致格式如下

int l=read(),r=read();
int x,y,z;
Split(rt,r,x,z);
Split(x,l-1,x,y);
Work(y);
Merge(Merge(x,y),z);

\(Work(y)\) 就是对以 \(y\) 为根的树进行具体操作。

---

直接上题

P3391 【模板】文艺平衡树

这道题求的是区间翻转。

很显然平衡树上直接翻等价于暴力。

但不要忘了利用相对平衡的树形结构。

而这让我们想到了线段树的区间操作。

对，没错，打标记，操作时下传。

而且我们发现：一段区间翻转两次后相当于没翻。

直接可以做了。

还是一棵平衡树，只是多了个信息（ \(tag\) ）。

struct Treap
{
	int val,rand,ls,rs,size,tag;
}tr[N];

\(tag\) 初始值为 \(0\) （表示没有反转）。

然后是 \(pushdown()\)

inline void pushdown(int p)
{
	if(!tr[p].tag) return;
	swap(tr[p].ls,tr[p].rs);//翻转序列==翻转下标
	//左右下传
	tr[tr[p].ls].tag^=1;
	tr[tr[p].rs].tag^=1;
	tr[p].tag=0;//不要忘了自身清零
}

\(pushdown()\) 一定要在递归下一层之前运行。

Split()

inline void Split(int p,int val,int &x,int &y)
{
	if(!p) return (void)(x=y=0);
	pushdown(p);//先下传
	if(tr[tr[p].ls].size+1<=val)//这里变了，比较下标就和Rank()差不多
	{
		x=p;
		Split(tr[p].rs,val-tr[tr[p].ls].size-1,tr[p].rs,y);//这里也不一样
	}
	else
	{
		y=p;
		Split(tr[p].ls,val,x,tr[p].ls);
	}
	Update(p);
}

Merge()

inline int Merge(int x,int y)
{
	if(!x||!y) return x+y;
	if(tr[x].rand<tr[y].rand)
	{
		pushdown(x);//先下传
		tr[x].rs=Merge(tr[x].rs,y);
		Update(x);return x;
	}
	else
	{
		pushdown(y);//先下传
		tr[y].ls=Merge(x,tr[y].ls);
		Update(y);return y;
	}
}

对于每一次询问

int l=read(),r=read();
int x,y,z;
Split(rt,r,x,z);
Split(x,l-1,x,y);
tr[y].tag^=1;//在树根打标记
rt=Merge(Merge(x,y),z);

最后根据二叉树的性质，中序遍历一遍平衡树就是原序列了。

献上完整代码。

#include <bits/stdc++.h>
#define re register
#define int long long
#define END system("pause")
#define inf 0x7fffffff
using namespace std;
inline int read()
{
	re int x=0,f=1;
	re char c=getchar();
	while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+c-48;c=getchar();}
	return x*f;
}
const int N=3e5+5,P=1e6;
int rt,num;
struct Treap{int val,rand,ls,rs,size,tag;}tr[N];
inline void Update(int x){tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;}
inline int New(int val){tr[++num]={val,rand(),0,0,1,0};return num;}
inline void pushdown(int p)
{
	if(!tr[p].tag) return;
	swap(tr[p].ls,tr[p].rs);
	tr[tr[p].ls].tag^=1;
	tr[tr[p].rs].tag^=1;
	tr[p].tag=0;
}
inline void Split(int p,int val,int &x,int &y)
{
	if(!p) return (void)(x=y=0);
	pushdown(p);
	if(tr[tr[p].ls].size+1<=val)
	{
		x=p;
		Split(tr[p].rs,val-tr[tr[p].ls].size-1,tr[p].rs,y);
	}
	else
	{
		y=p;
		Split(tr[p].ls,val,x,tr[p].ls);
	}
	Update(p);
}
inline int Merge(int x,int y)
{
	if(!x||!y) return x+y;
	if(tr[x].rand<tr[y].rand)
	{
		pushdown(x);
		tr[x].rs=Merge(tr[x].rs,y);
		Update(x);return x;
	}
	else
	{
		pushdown(y);
		tr[y].ls=Merge(x,tr[y].ls);
		Update(y);return y;
	}
}
inline void Insert(int val)
{
	int x,y;
	Split(rt,val,x,y);
	rt=Merge(Merge(x,New(val)),y);
}
inline void dfs(int p)//中序遍历
{
	pushdown(p);//遍历前先下传
	if(tr[p].ls) dfs(tr[p].ls);
	printf("%d ",tr[p].val);
	if(tr[p].rs) dfs(tr[p].rs);
}
signed main()
{
	srand(98244353);
	int n=read(),m=read();
	for(re int i=1;i<=n;++i) Insert(i);
	while(m--)
	{
		int l=read(),r=read();
		int x,y,z;
		Split(rt,r,x,z);Split(x,l-1,x,y);
		tr[y].tag^=1;
		rt=Merge(Merge(x,y),z);
	}
	dfs(rt);
	//END;
	return 0;
}

个人认为区间操作挺好理解的。

---

可持续化

我们发现在进行 \(Split()\) ， \(Merge()\) 操作时，我们其实就只是变动了原树的不到一半，而我们完全可以在剩下的节点上建立新的节点来可持续化。

从网上嚯了一张图片：

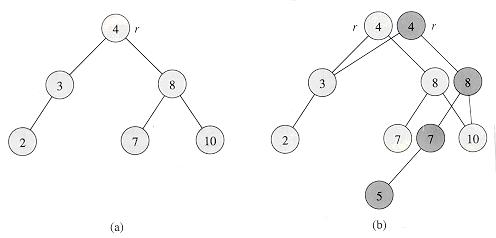
如图，深色 \(4\) ，\(8\) ，\(7\) 为新建节点，\(5\) 为新插入的节点。

于是：

Split()

inline void Split(int p,int val,int &x,int &y)
{
	if(!p) return (void)(x=y=0);
	if(tr[p].val<=val)
	{
		x=New(0);//x为新建节点
		tr[x]=tr[p];
		Split(tr[x].rs,val,tr[x].rs,y);
		Update(x);//与之前不同，由于x为独立的节点，与下面的y没有关系，所以要各自单独Update()
	}
	else
	{
		y=New(0);
		tr[y]=tr[p];
		Split(tr[y].ls,val,x,tr[y].ls);
		Update(y);
	}
}

Merge()

inline int Merge(int x,int y)
{
	if(!x||!y) return x+y;
	if(tr[x].rand<tr[y].rand)
	{
		int p=New(0);//这里也是，新建节点
		tr[p]=tr[x];
		tr[p].rs=Merge(tr[p].rs,y);
		Update(p);
		return p;
	}
	int p=New(0);
	tr[p]=tr[y];
	tr[p].ls=Merge(x,tr[p].ls);
	Update(p);
	return p;
}

---

上题

P3835 【模板】可持久化平衡树

只需将 \(rt\) 开成数组，保存每个时刻的根，然后其他操作都在普通平衡树上稍微改一下即可。

#include <bits/stdc++.h>
#define re register
//#define int long long
#define lss tr[p].ls
#define rss tr[p].rs
#define END system("pause")
#define inf 0x7fffffff
using namespace std;
inline int read()
{
	re int x=0,f=1;
	re char c=getchar();
	while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+c-48;c=getchar();}
	return x*f;
}
const int N=5e5+5;
int num;
int rt[N];
struct Treap{int val,rand,ls,rs,size;}tr[N<<6];
inline int New(int val)
{
	tr[++num]={val,rand(),0,0,1};
	return num;
}
inline void Update(int p)
{
	tr[p].size=tr[lss].size+tr[rss].size+1;
}
inline void Split(int p,int val,int &x,int &y)
{
	if(!p) return (void)(x=y=0);
	if(tr[p].val<=val)
	{
		x=New(0);
		tr[x]=tr[p];
		Split(tr[x].rs,val,tr[x].rs,y);
		Update(x);
	}
	else
	{
		y=New(0);
		tr[y]=tr[p];
		Split(tr[y].ls,val,x,tr[y].ls);
		Update(y);
	}
}
inline int Merge(int x,int y)
{
	if(!x||!y) return x+y;
	if(tr[x].rand<tr[y].rand)
	{
		int p=New(0);
		tr[p]=tr[x];
		tr[p].rs=Merge(tr[p].rs,y);
		Update(p);
		return p;
	}
	int p=New(0);
	tr[p]=tr[y];
	tr[p].ls=Merge(x,tr[p].ls);
	Update(p);
	return p;
}
inline void Insert(int ver,int val)
{
	int x,y;
	Split(rt[ver],val-1,x,y);
	rt[ver]=Merge(Merge(x,New(val)),y);
}
inline void Delete(int ver,int val)
{
	int x,y,z;
	Split(rt[ver],val,x,z);Split(x,val-1,x,y);
	y=Merge(tr[y].ls,tr[y].rs);
	rt[ver]=Merge(Merge(x,y),z);
}
inline int Rank(int ver,int val)
{
	int x,y,anss;
	Split(rt[ver],val-1,x,y);
	anss=tr[x].size+1;
	rt[ver]=Merge(x,y);
	return anss;
}
inline int Find(int p,int Kth)
{
	if(tr[lss].size+1==Kth) return p;
	if(Kth<=tr[lss].size) return Find(lss,Kth);
	return Find(rss,Kth-tr[lss].size-1);
}
inline int Pre(int ver,int val)
{
	int x,y,anss;
	Split(rt[ver],val-1,x,y);
	anss=tr[Find(x,tr[x].size)].val;
	rt[ver]=Merge(x,y);
	return anss;
}
inline int Next(int ver,int val)
{
	int x,y,anss;
	Split(rt[ver],val,x,y);
	anss=tr[Find(y,1)].val;
	rt[ver]=Merge(x,y);
	return anss;
}
signed main()
{
	int T=read();
	for(re int i=1;i<=T;++i)
	{
		int ver=read(),op=read(),val=read();
		rt[i]=rt[ver];
		if(op==1) Insert(i,val);
		else if(op==2) Delete(i,val);
		else if(op==3) printf("%d\n",Rank(i,val));
		else if(op==4) printf("%d\n",tr[Find(rt[i],val)].val);
		else if(op==5) printf("%d\n",Pre(i,val));
		else printf("%d\n",Next(i,val));
	}
	return 0;
}

---

后记

后面还有一些更高级的操作，蒟蒻太弱了根本不会，还请大佬自行研究。

这里附上几道题目：

P5055 【模板】可持久化文艺平衡树

P2042 [NOI2005] 维护数列（这是一道毒瘤题）

P1486 [NOI2004] 郁闷的出纳员

P2286 [HNOI2004]宠物收养场

乌拉！！！