[cf1444D]Rectangular Polyline

由于两种线段要交替出现，有解的必要条件即为$h=v$（以下均记为$n$）

进一步的，再假设两种线段依次对应于向量$(a_{i},0)$和$(0,b_{i})$，根据题意要求向量长度为给定值且和为0，那么也即有$|a_{i}|=l_{i},|b_{i}|=p_{i}$且$\sum_{i=1}^{n}a_{i}=\sum_{i=1}^{n}b_{i}=0$

使用背包判定是否存在这样的$a_{i}$和$b_{i}$，若不存在即无解，若存在则再求出任意一组

（可以证明此时一定有解，以下即为构造）

若$a_{i}$中的负数少于$b_{i}$则将两者全部取相反数，再将两者分别从大到小排序（其实只需要保证正数在负数前），最后将$(a_{i},b_{i})$作为一个整体极角排序，并依次选择$(a_{1},0),(0,b_{1}),(a_{2},0),...,(b_{n},0)$即可

（代码实现上通过将两边分别合理排序使得其已经极角排序）

不难发现，以此法最终方案一定是形如下图的形式，即合法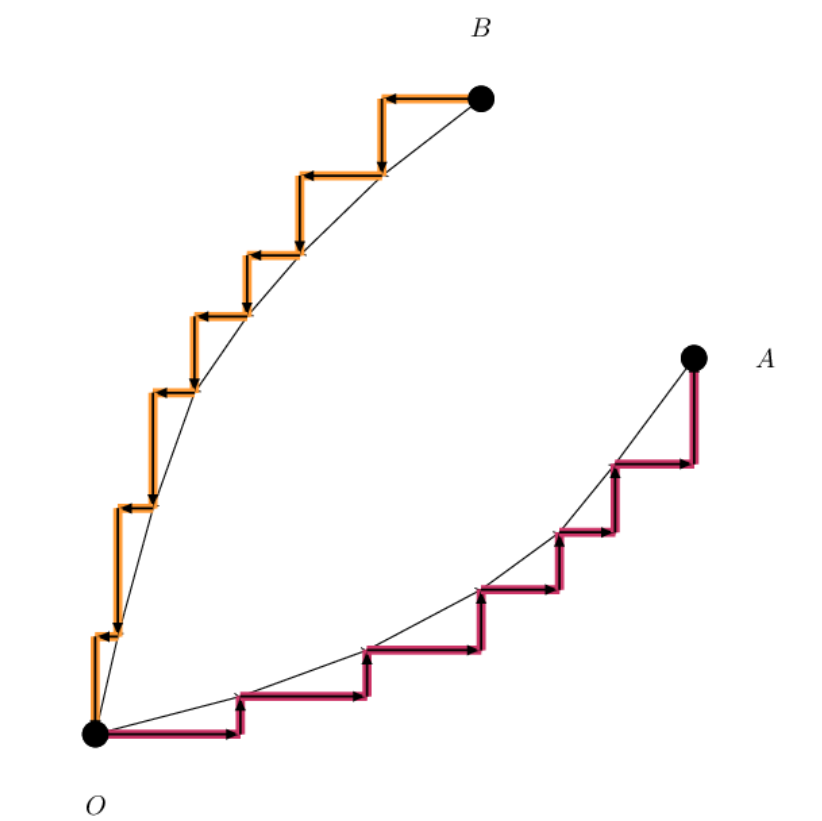

时间复杂度为$o(\frac{nC^{2}}{\omega})$，可以通过

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 #define N 1005
 4 bitset<N*N>f[N];
 5 int t,n,m,a[N],b[N];
 6 int calc(int *a){
 7     int m=0;
 8     for(int i=1;i<=n;i++)m+=a[i];
 9     if (m&1)return 0;
10     m>>=1;
11     for(int i=1;i<=n;i++)f[i]=((f[i-1])|(f[i-1]<<a[i]));
12     if (!f[n][m])return 0;
13     for(int i=n;i;i--)
14         if (!f[i-1][m]){
15             m-=a[i];
16             a[i]=-a[i];
17         }
18     return 1;
19 }
20 int main(){
21     f[0][0]=1;
22     scanf("%d",&t);
23     while (t--){
24         scanf("%d",&n);
25         for(int i=1;i<=n;i++)scanf("%d",&a[i]);
26         scanf("%d",&m);
27         for(int i=1;i<=m;i++)scanf("%d",&b[i]);
28         if ((n!=m)||(!calc(a))||(!calc(b))){
29             printf("No\n");
30             continue;
31         }
32         int cnt=0;
33         for(int i=1;i<=n;i++)cnt+=(a[i]<0)-(b[i]<0);
34         if (cnt<0){
35             for(int i=1;i<=n;i++)a[i]=-a[i],b[i]=-b[i];
36         }
37         sort(a+1,a+n+1),reverse(a+1,a+n+1);
38         sort(b+1,b+n+1),reverse(b+1,b+n+1);
39         for(int i=1;i<=n+1;i++)
40             if ((i>n)||(a[i]<0)){
41                 reverse(b+1,b+i);
42                 break;
43             }
44         for(int i=n;i>=0;i--)
45             if ((!i)||(b[i]>0)){
46                 reverse(a+i+1,a+n+1);
47                 break;
48             }
49         printf("Yes\n");
50         for(int i=1,x=0,y=0;i<=n;i++){
51             x+=a[i],printf("%d %d\n",x,y);
52             y+=b[i],printf("%d %d\n",x,y);
53         }
54     }
55     return 0;
56 }