List（JDK1.7）（2）
LinkedList
List接口和Deque接口的一种双向链表实现。非同步的。
快速失败机制。ConcurrentModificationException
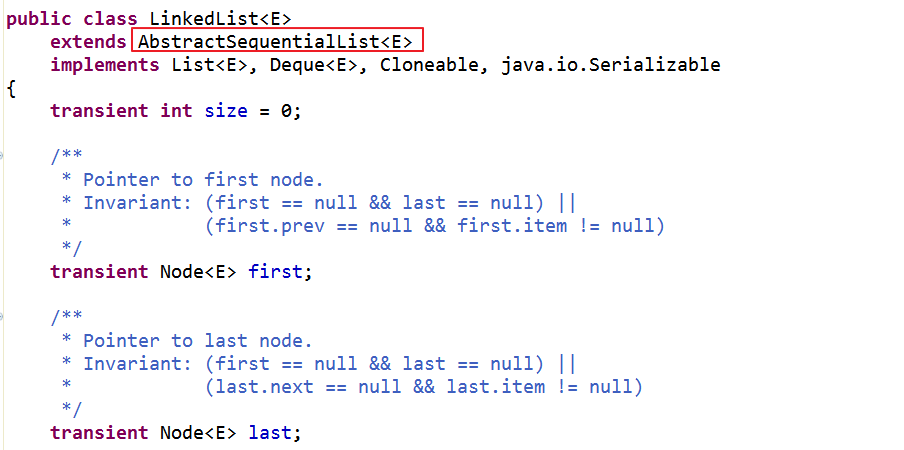
结点结构
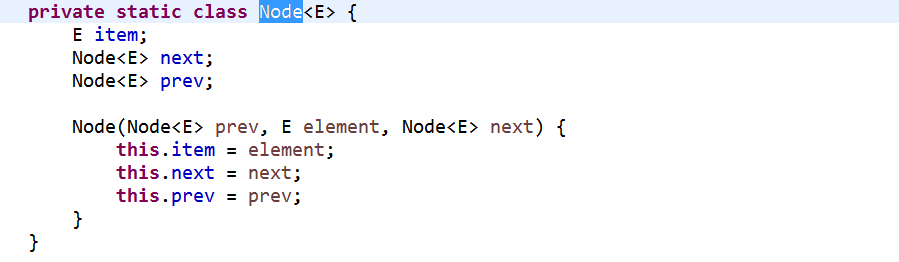
插入结点
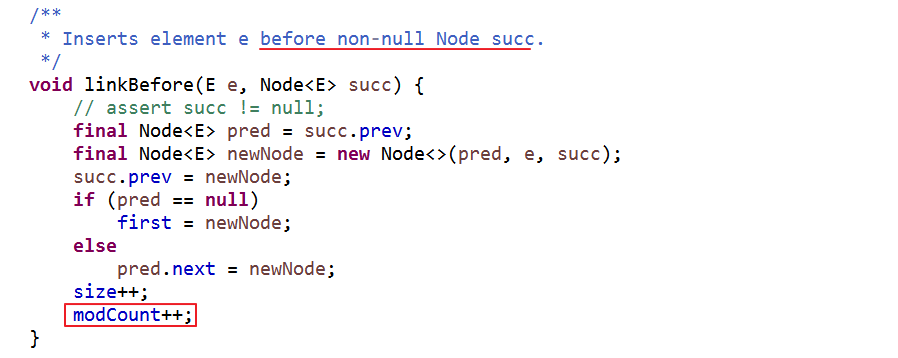
删除结点
add()
remove()
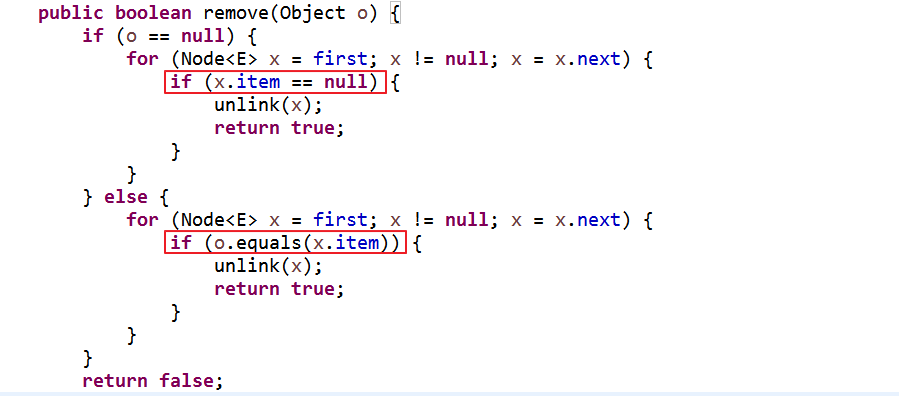
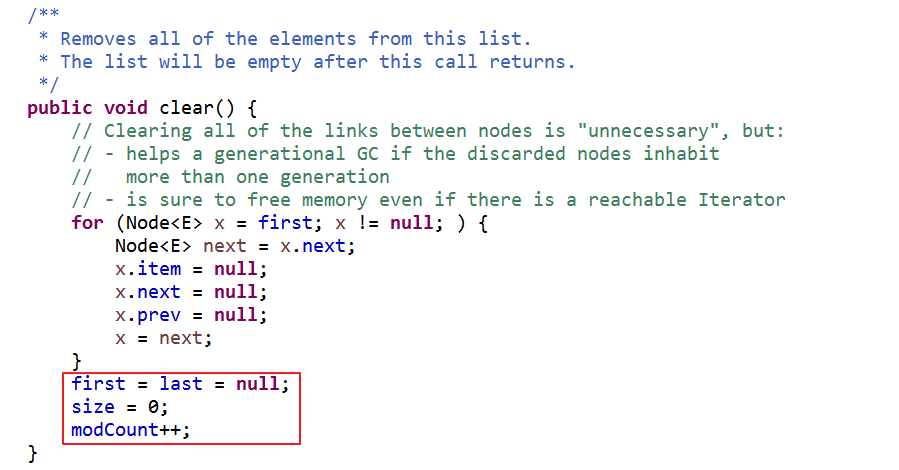
clear()
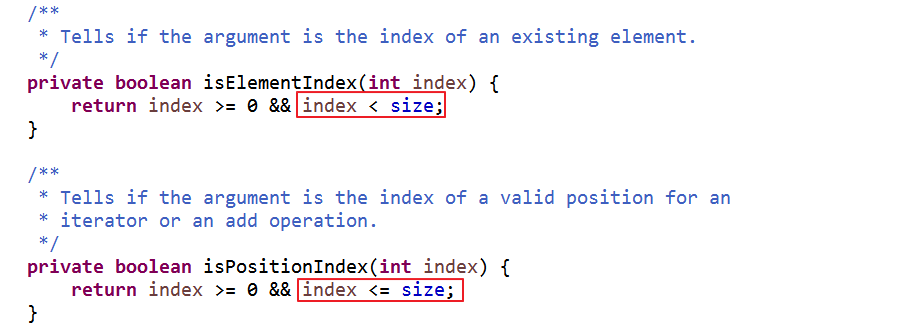
get()
set()
和队列相关的操作
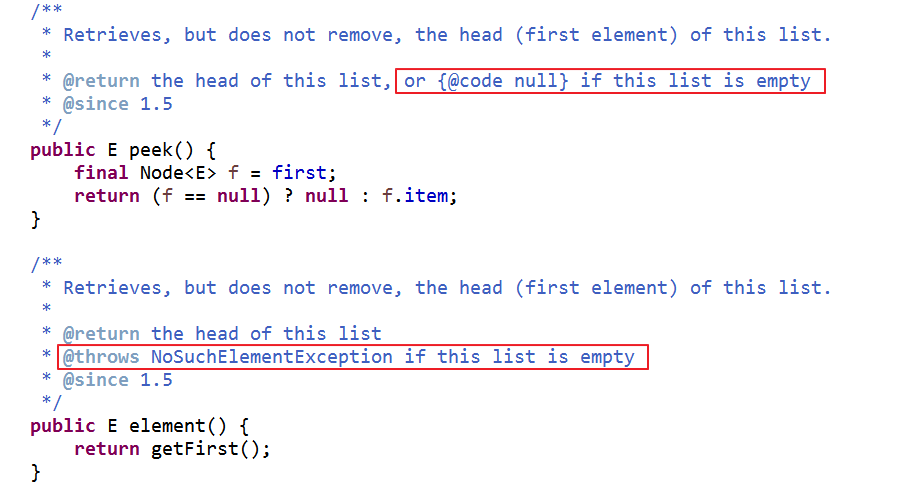
peek() 和 element()
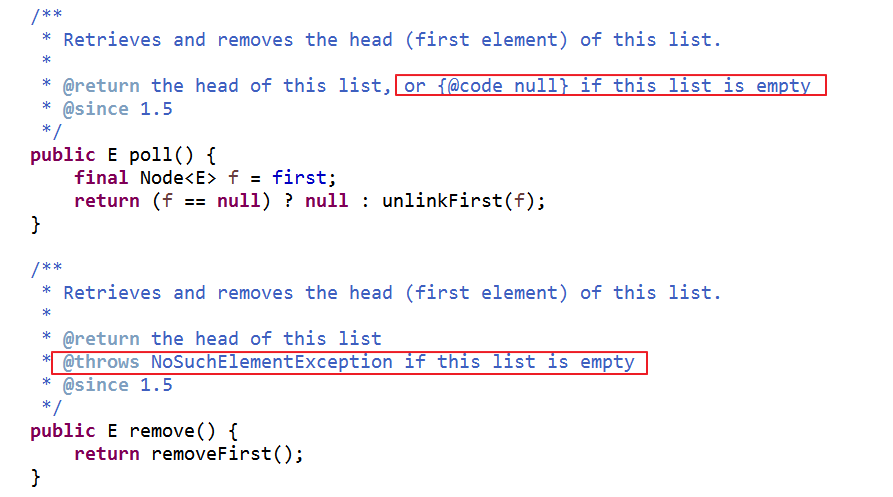
poll() 和 remove()
offer()
和栈相关的操作
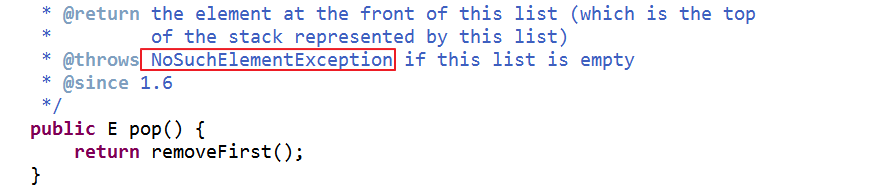
迭代器
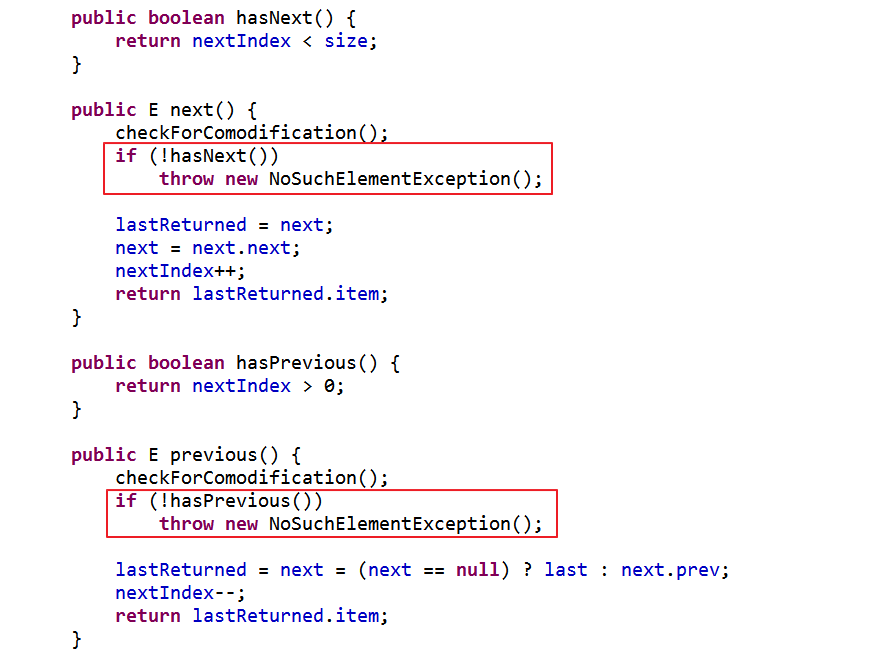
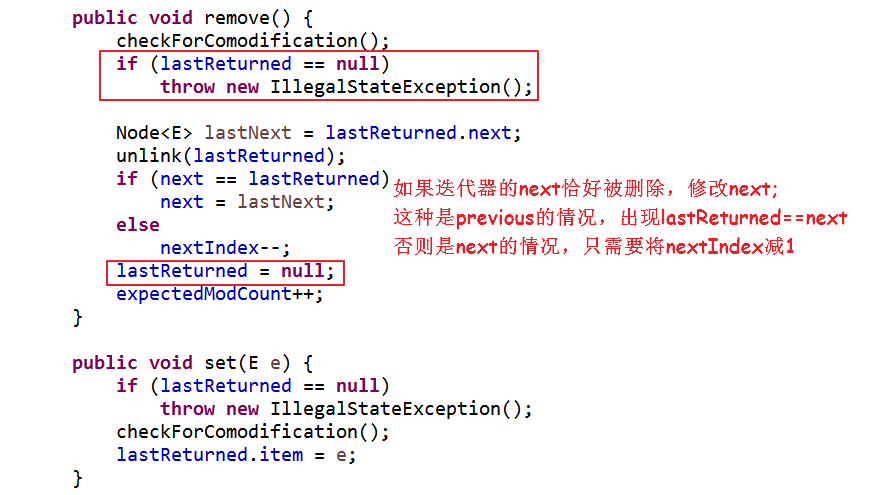
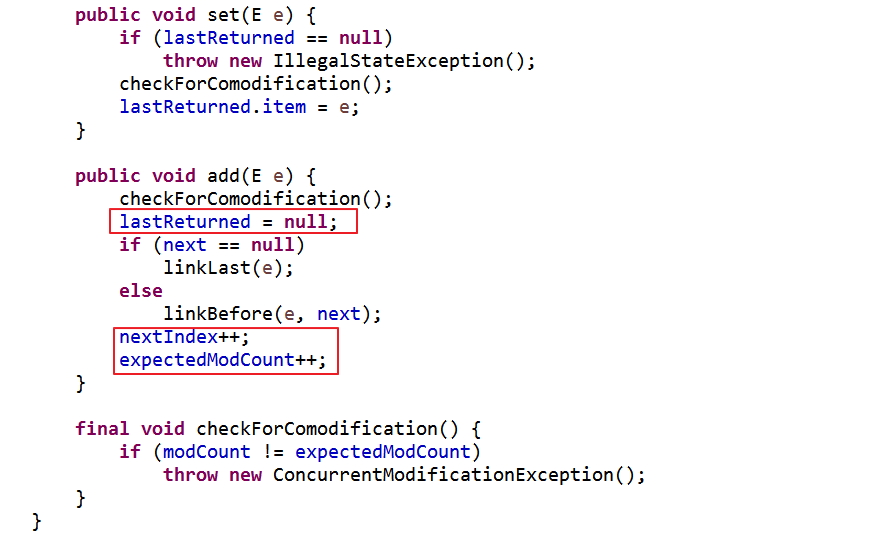
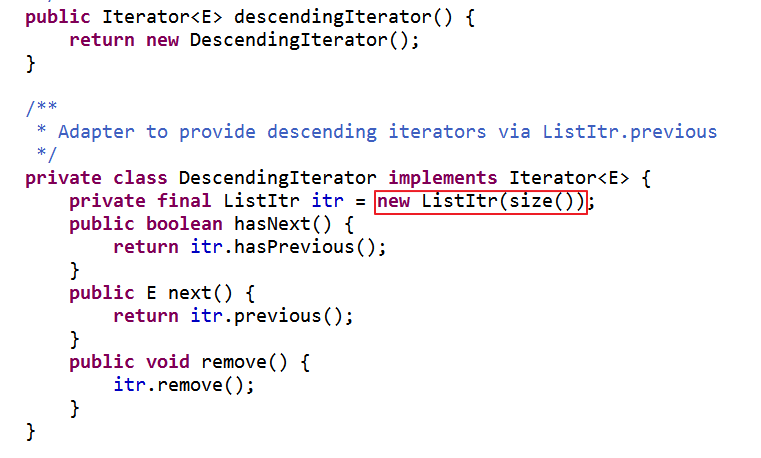
降序迭代器
List（JDK1.7）（2）的更多相关文章
- Java集合：ArrayList （JDK1.8 源码解读）
ArrayList ArrayList几乎是每个java开发者最常用也是最熟悉的集合,看到ArrayList这个名字就知道,它必然是以数组方式实现的集合 关注点 说一下ArrayList的几个特点,也 ...
- Web service project中导入的库JAXB（JDK1.7新产品,组成部分）
JAXB(Java Architecture for XML Binding) 是一个业界的标准,是一项可以根据XML Schema产生Java类的技术.该过程中,JAXB也提供了将XML实例文档反向 ...
- Java集合：LinkedList （JDK1.8 源码解读）
LinkedList介绍 还是和ArrayList同样的套路,顾名思义,linked,那必然是基于链表实现的,链表是一种线性的储存结构,将储存的数据存放在一个存储单元里面,并且这个存储单元里面还维护了 ...
- 导入一个新项目需要注意的几大问题（jdk1.6+eclipse4.4+tomcat6）
今天导项目犯了一个很低级的错误,浪费了半个小时,所以在此罗列出在导一个新的项目到eclipse中时需要注意的几个问题,希望对大家有所帮助. 将项目从svn或者github等项目版本控制软件上拷贝下来, ...
- HashMap源码（JDK1.8）-手动注释
HashMap简介 HashMap是一种K-V映射的一种数据结构,通过K(key)值能实现在O(1)的时间复杂度下找到对应的V(value).JDK1.8之前,HashMap的底层数据结构是数组+链表 ...
- java基础知识回顾之java Thread类学习（八）--java.util.concurrent.locks（JDK1.5）与synchronized异同讲解
看API文档介绍几个方法: JDK1.5中提供了多线程的升级解决方案: 特点: 1.将同步synchronized显示的替换成Lock 2.接口Conditio ...
- javase基础回顾（一）ArrayList深入解析 解读ArrayList源代码（JDK1.8.0_92）
我们在学习这一块内容时需要注意的一个问题是 集合中存放的依然是对象的引用而不是对象本身. List接口扩展了Collection并声明存储一系列元素的类集的特性.使用一个基于零的下标,元素可以通过它们 ...
- ConcurrentHashMap源码解析（JDK1.8）
package java.util.concurrent; import java.io.ObjectStreamField; import java.io.Serializable; import ...
- 使用ArrayList时代码内部发生了什么（jdk1.7）？
前言 ArrayList(这里的ArrayList是基于jdk1.7)是在项目中经常使用的集合类,例如我们从数据库中查询出一组数据.这篇文章不去剖析它的继承和实现,只是让我们知道实例化及增删改查时它的 ...
- Java基础系列--HashMap（JDK1.8）
原创作品,可以转载,但是请标注出处地址:https://www.cnblogs.com/V1haoge/p/10022092.html Java基础系列-HashMap 1.8 概述 HashMap是 ...
随机推荐
- Alpha阶段综合报告
1.版本测试报告 1.1在测试过程中总共发现了多少Bug?每个类别的Bug分别为多少个? Bug分类 Bug内容 Fixed 编辑博文时改变文字格式会刷新界面 Can’t reproduced 无 N ...
- week2：个人博客作业
1.这周写程序感想: 昨天差不多,也是这个时候看些的程序,写了4个小时程序,感触颇多.昨日,原打算,就完成程序就吧这个随笔写完结果,由于各种原因,没写一直拖到现在.就做昨天写的程序,本身题目很简单,主 ...
- [转帖]nvidia nvlink互联与nvswitch介绍
nvidia nvlink互联与nvswitch介绍 https://www.chiphell.com/thread-1851449-1-1.html 差不多在一个月前在年度gtc会议上,老黄公开了d ...
- 二分图最大匹配模板（pascal）
uoj#78. 二分图最大匹配 从前一个和谐的班级,有 nlnl 个是男生,有 nrnr 个是女生.编号分别为 1,…,nl1,…,nl 和 1,…,nr1,…,nr. 有若干个这样的条件:第 vv ...
- BZOJ3289 Mato的文件管理（莫队+树状数组）
这个做法非常显然. #include<iostream> #include<cstdio> #include<cmath> #include<cstdlib& ...
- CF915E Physical Education Lessons
题意: Alex高中毕业了,他现在是大学新生.虽然他学习编程,但他还是要上体育课,这对他来说完全是一个意外.快要期末了,但是不幸的Alex的体育学分还是零蛋! Alex可不希望被开除,他想知道到期末还 ...
- Day22-Django之缓存
由于Django是动态网站,所有每次请求均会去数据进行相应的操作,当程序访问量大时,耗时必然会更加明显,最简单解决方式是使用:缓存,缓存将一个某个views的返回值保存至内存或者memcache中,5 ...
- ORA-01034和ORA-27101的解决方法
问题所在: 1.要登录的数据库实例内容配置内容错误,联系负责该机子的管理员看原因
- 模板：快速傅里叶变换（FFT）
参考:http://blog.csdn.net/f_zyj/article/details/76037583 如果公式炸了请去我的csdn博客:http://blog.csdn.net/luyouqi ...
- 【NOI 2018】冒泡排序（组合数学）
题意大概是给定一个长度为$n$的排列$p$,求有多少长度为$n$的排列满足冒泡排序的交换次数为$\frac{1}{2} \sum\limits_{i = 1}^{n}|i - p_{i}|$. 可以发 ...