Java实现链式存储的二叉查找树（递归方法）

二叉查找树的定义：

　　二叉查找树或者是一颗空树，或者是一颗具有以下特性的非空二叉树：

　　　　1. 若左子树非空，则左子树上所有节点关键字值均小于根节点的关键字；

　　　　2. 若右子树非空，则右子树上所有节点关键字值均大于根节点的关键字；

　　　　3. 左、右子树本身也分别是一颗二叉查找树。

二叉查找树的实现，功能有：

　　1. 用一个数组去构建二叉查找树

　　2. 二叉查找树的中序遍历和层次遍历

　　3. 插入节点

　　4. 查找节点

5. 查找二叉树中的最大值和最小值

　　6.  得到节点的直接父节点

　　7. 得到节点的直接前驱和直接后继节点

　　8. 删除节点

树节点TreeNode的定义见：Java实现链式存储的二叉树

 import java.lang.Integer;
 import java.util.LinkedList;
 import java.util.Queue;
 import java.util.Scanner;

 /*
  * 二叉排序树（二叉查找树）的实现
  */
 public class BinarySearchTree {
     private TreeNode<Integer> root;  //根节点

     public BinarySearchTree(){
         root = null;
     }

     //用一个数组去构建二叉查找树
     public TreeNode<Integer> buildBST(Integer[] array){
         if(array.length == 0){
             return null;
         }else{
             root = null;  //初始化树为空树
             for(int i=0; i<array.length; i++){ //依次将每个元素插入
                 root = insertNode(root,array[i]);
             }
             return root;
         }
     }

     //在二叉查找树中插入一个数据域为data的结点，新插入的结点一定是某个叶子节点
     public TreeNode<Integer> insertNode(TreeNode<Integer> node, Integer data){
         if(node == null){   //原树为空，新插入的记录为根节点
             node = new TreeNode<Integer>(data,null,null);
         }else{
             if(node.getData() == data){   //树中存在相同关键字的结点,什么也不做

             }else{
                 if(node.getData() > data){  //根节点>插入数据，插入到左子树中
                     node.setLchild(insertNode(node.getLchild(),data));
                 }else{ //根节点<插入数据，插入到右子树中
                     node.setRchild(insertNode(node.getRchild(),data));
                 }
             }
         }
         return node;
     }

     //二叉查找树的中序遍历，可以得到一个递增的有序数列
     public void inOrder(TreeNode<Integer> node){
         if(node != null){
             inOrder(node.getLchild());
             System.out.print(node.getData()+" ");
             inOrder(node.getRchild());
         }
     }
     //二叉查找树的层次遍历
     public void levelOrder(TreeNode<Integer> root){
         Queue<TreeNode<Integer>> nodeQueue = new LinkedList<TreeNode<Integer>>();
         TreeNode<Integer> node = null;
         nodeQueue.add(root);  //将根节点入队
         while(!nodeQueue.isEmpty()){  //队列不空循环
             node = nodeQueue.peek();
             System.out.print(node.getData()+" ");
             nodeQueue.poll();     //队头元素出队
             if(node.getLchild() != null){     //左子树不空，则左子树入队列
                 nodeQueue.add(node.getLchild());
             }
             if(node.getRchild() != null){     //右子树不空，则右子树入队列
                 nodeQueue.add(node.getRchild());
             }
         }
     }

     //查找数据域为data的结点，若不存在，返回null
     public TreeNode<Integer> searchNode(TreeNode<Integer> node, Integer data){
         while(node != null && node.getData() != data){
             if(node.getData() > data){
                 node = node.getLchild();  //根节点>数据，向左走
             }else{
                 node = node.getRchild();  //根节点<数据，向右走
             }
         }
         return node;
     }

     //查找最大值：不断地寻找右子节点
     public TreeNode<Integer> getMaxData(TreeNode<Integer> node){
         if(node.getRchild() == null){
             return node;
         }else{
             return getMaxData(node.getRchild());
         }
     }

     //查找最小值：不断地寻找左子节点
     public TreeNode<Integer> getMinData(TreeNode<Integer> node){
         if(node.getLchild() == null){
             return node;
         }else{
             return getMinData(node.getLchild());
         }
     }

     //得到数据域为data的结点的直接父节点parentNode
     public TreeNode<Integer> getParentNode(TreeNode<Integer> root, Integer data){
         TreeNode<Integer> parentNode = root;
         if(parentNode.getData() == data){   //根节点的父节点返回为null
             return null;
         }
         while(parentNode != null){
             //查找当前节点的父节点的左右子节点，若是相等，则返回该父节点
             if((parentNode.getLchild() != null && parentNode.getLchild().getData() == data) ||
                     (parentNode.getRchild() != null && parentNode.getRchild().getData() == data)){
                 return parentNode;
             }else{
                 if(parentNode.getData() > data){ //向左查找父节点
                     parentNode = parentNode.getLchild();
                 }else{
                     parentNode = parentNode.getRchild();  //向右查找父节点
                 }
             }
         }
         return null;
     }

     /**
      * 得到结点node的直接前趋
      * a.该节点左子树不为空：其前驱节点为其左子树的最大元素
      * b.该节点左子树为空: 其前驱节点为其祖先节点(递归)，且该祖先节点的右孩子也为其祖先节点
      *   (就是一直往其parent找，出现左拐后的那个祖先节点)
      */
     public TreeNode<Integer> getPrecessor(TreeNode<Integer> root,TreeNode<Integer> node){
         if(node == null){
             return null;
         }
         //a.该节点左子树不为空：其前驱节点为其左子树的最大元素
         if(node.getLchild() != null){
             return getMaxData(node.getLchild());
         }else{  //b.该节点左子树为空: 其前驱节点为其祖先节点(递归)
             TreeNode<Integer> parentNode = getParentNode(root, node.getData());
             while(parentNode != null && node == parentNode.getLchild()){
                 node = parentNode;
                 parentNode = getParentNode(root, parentNode.getData());
             }
             return parentNode;
         }
     }

     /**
      * 得到结点node的直接后继(后继节点就是比要删除的节点的关键值要大的节点集合中的最小值)
      * a.该节点右子树不为空，其后继节点为其右子树的最小元素
      * b.该节点右子树为空，则其后继节点为其祖先节点(递归)，且此祖先节点的左孩子也是该节点的祖先节点，
      *   就是说一直往上找其祖先节点，直到出现右拐后的那个祖先节点：
      */
     public TreeNode<Integer> getSuccessor(TreeNode<Integer> root,TreeNode<Integer> node){
         if(node == null){
             return null;
         }
         //a.该节点右子树不为空，其后继节点为其右子树的最小元素
         if(node.getRchild() != null){
             return getMinData(node.getRchild());
         }else{  //b.该节点右子树为空，则其后继节点为其最高祖先节点(递归)
             TreeNode<Integer> parentNode = getParentNode(root, node.getData());
             while(parentNode != null && node == parentNode.getRchild()){
                 node = parentNode;
                 parentNode = getParentNode(root, parentNode.getData());
             }
             return parentNode;
         }
     }

     /**
      * 删除数据域为data的结点
      * 按三种情况处理：
      * a.如果被删除结点z是叶子节点，则直接删除，不会破坏二叉查找树的性质
      * b.如果节点z只有一颗左子树或右子树，则让z的子树成为z父节点的子树，代替z的位置
      * c.若结点z有左、右两颗子树，则令z的直接后继（或直接前驱）替代z，
      *   然后从二叉查找树中删去这个直接后继（或直接前驱）,这样就转换为第一或第二种情况
      * @param node 二叉查找树的根节点
      * @param data 需要删除的结点的数据域
      * @return
      */
     public boolean deleteNode(TreeNode<Integer> node, Integer data){
         if(node == null){ //树为空
             throw new RuntimeException("树为空！");
         }
         TreeNode<Integer> delNode= searchNode(node, data);  //搜索需要删除的结点
         TreeNode<Integer> parent = null;
         if(delNode == null){  //如果树中不存在要删除的关键字
             throw new RuntimeException("树中不存在要删除的关键字！");
         }else{
             parent = getParentNode(node,data);  //得到删除节点的直接父节点
             //a.如果被删除结点z是叶子节点，则直接删除，不会破坏二叉查找树的性质
             if(delNode.getLchild()==null && delNode.getRchild()==null){
                 if(delNode==parent.getLchild()){  //被删除节点为其父节点的左孩子
                     parent.setLchild(null);
                 }else{    //被删除节点为其父节点的右孩子
                     parent.setRchild(null);
                 }
                 return true;
             }
             //b1.如果节点z只有一颗左子树，则让z的子树成为z父节点的子树，代替z的位置
             if(delNode.getLchild()!=null && delNode.getRchild()==null){
                 if(delNode==parent.getLchild()){ //被删除节点为其父节点的左孩子
                     parent.setLchild(delNode.getLchild());
                 }else{ //被删除节点为其父节点的右孩子
                     parent.setRchild(delNode.getLchild());
                 }
                 delNode.setLchild(null); //设置被删除结点的左孩子为null
                 return true;
             }
             //b2.如果节点z只有一颗右子树，则让z的子树成为z父节点的子树，代替z的位置
             if(delNode.getLchild()==null && delNode.getRchild()!=null){
                 if(delNode==parent.getLchild()){ //被删除节点为其父节点的左孩子
                     parent.setLchild(delNode.getRchild());
                 }else{  //被删除节点为其父节点的右孩子
                     parent.setRchild(delNode.getRchild());
                 }
                 delNode.setRchild(null); //设置被删除结点的右孩子为null
                 return true;
             }
             //c.若结点z有左、右两颗子树，则删除该结点的后继结点，并用该后继结点取代该结点
             if(delNode.getLchild()!=null && delNode.getRchild()!=null){
                 TreeNode<Integer> successorNode = getSuccessor(node,delNode); //得到被删除结点的后继节点
                 deleteNode(node,successorNode.getData()); //删除该结点的后继结点
                 delNode.setData(successorNode.getData()); //用该后继结点取代该结点
                 return true;
             }
         }
         return false;
     }

     public static void main(String args[]){
         Scanner input = new Scanner(System.in);
         Integer[] array = {8,3,10,1,6,14,4,7,13};
         BinarySearchTree bst = new BinarySearchTree();
         TreeNode<Integer> root = bst.buildBST(array);
         System.out.print("层次遍历：");
         bst.levelOrder(root);
         System.out.print("\n"+"中序遍历：");
         bst.inOrder(root);
          System.out.println();
          System.out.print("得到最大值：");
          System.out.println(bst.getMaxData(root).getData());
          System.out.print("得到最小值：");
          System.out.println(bst.getMinData(root).getData());
          System.out.print("向二叉查找树中插入一个节点，请输入需插入节点的数据域：");
          int data = input.nextInt();
          System.out.print("插入节点"+ data +"后，中序遍历的结果：");
          root = bst.insertNode(root, data);
          bst.inOrder(root);
          System.out.println("\n"+"在二叉查找树中查找元素,"+"请输入需要查找的结点值：");
          data = input.nextInt();
          if(bst.searchNode(root, data) == null){
              System.out.println("false");
          }else{
              System.out.println("true");
          }
          System.out.println("查找节点的直接父节点,"+"请输入需要查找的结点值：");
          data = input.nextInt();
          System.out.print("节点"+ data +"的父节点是：");
          if(bst.getParentNode(root, data) == null){
              System.out.println("null");
          }else{
              System.out.println(bst.getParentNode(root, data).getData());
          }
          System.out.println("删除结点,"+"请输入需要删除的结点值：");
          data = input.nextInt();
          if(bst.deleteNode(root, data)){
             System.out.print("删除结点后的层次遍历：");
              bst.levelOrder(root);
              System.out.print("\n"+"删除结点后的中序遍历：");
              bst.inOrder(root);
          }
     }
 }

程序运行结果：

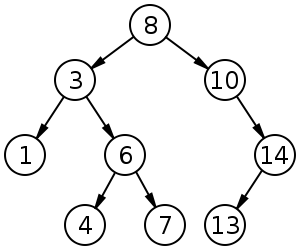
层次遍历：8 3 10 1 6 14 4 7 13
中序遍历：1 3 4 6 7 8 10 13 14
得到最大值：14
得到最小值：1
向二叉查找树中插入一个节点，请输入需插入节点的数据域：15
插入节点15后，中序遍历的结果：1 3 4 6 7 8 10 13 14 15
在二叉查找树中查找元素,请输入需要查找的结点值：
4
true
查找节点的直接父节点,请输入需要查找的结点值：
10
节点10的父节点是：8
删除结点,请输入需要删除的结点值：
4
删除结点后的层次遍历：8 3 10 1 6 14 7 13 15
删除结点后的中序遍历：1 3 6 7 8 10 13 14 15 

某些方法的非递归实现：

1. 插入节点insertNode():

 　　//在二叉查找树中插入一个数据域为data的结点，新插入的结点一定是某个叶子节点
     public TreeNode<Integer> insertNode(TreeNode<Integer> node, Integer data){
         TreeNode<Integer> newNode = new TreeNode<Integer>(data,null,null);
         TreeNode<Integer> tmpNode = node;  //遍历节点
         TreeNode<Integer> pnode = null;   //记录当前节点的父节点    

         if(node == null){   //原树为空，新插入的记录为根节点
             node = newNode;
             return node;
         }
         while(tmpNode != null){
             pnode = tmpNode;
             if(tmpNode.getData() == data){ //树中存在相同关键字的结点,什么也不做
                 return node;
             }else{
                 if(tmpNode.getData() > data){ //根节点>插入数据，插入到左子树中
                     tmpNode = tmpNode.getLchild();
                 }else{ //根节点<插入数据，插入到右子树中
                     tmpNode = tmpNode.getRchild();
                 }
             }
         }
         if(pnode.getData() > data){
             pnode.setLchild(newNode);
         }else{
             pnode.setRchild(newNode);
         }
         return node;
     }

2. 二叉查找树的中序遍历：

 　　//二叉查找树的中序遍历LNR，可以得到一个递增的有序数列
     public void inOrder(TreeNode<Integer> node){
         Stack<TreeNode<Integer>> nodeStack = new Stack<TreeNode<Integer>>();
         TreeNode<Integer> tempNode = node;  //遍历指针
         while(tempNode != null || !nodeStack.isEmpty()){
             if(tempNode != null){
                 nodeStack.push(tempNode);
                 tempNode = tempNode.getLchild();
             }else{
                 tempNode = nodeStack.pop();
                 System.out.print(tempNode.getData() + " ");
                 tempNode = tempNode.getRchild();
             }
         }
     }

3. 得到二叉查找树的最大值和最小值：

     //查找最大值：不断地寻找右子节点
     public TreeNode<Integer> getMaxData(TreeNode<Integer> node){
         TreeNode<Integer> tempNode = node;
         while(tempNode.getRchild()!=null){
             tempNode = tempNode.getRchild();
         }
         return tempNode;
     }

     //查找最小值：不断地寻找左子节点
     public TreeNode<Integer> getMinData(TreeNode<Integer> node){
         TreeNode<Integer> tempNode = node;
         while(tempNode.getLchild() != null){
             tempNode = tempNode.getLchild();
         }
         return tempNode;
     }