CodeForces 445B. DZY Loves Chemistry（并查集）

转载请注明出处:http://blog.csdn.net/u012860063?viewmode=contents

题目链接：http://codeforces.com/problemset/problem/445/B

----------------------------------------------------------------------------------------------------------------------------------------------------------

欢迎光临天资小屋：http://user.qzone.qq.com/593830943/main

----------------------------------------------------------------------------------------------------------------------------------------------------------

DZY loves chemistry, and he enjoys mixing chemicals.

DZY has n chemicals, and m pairs of them will react.
He wants to pour these chemicals into a test tube, and he needs to pour them in one by one, in any order.

Let's consider the danger of a test tube. Danger of an empty test tube is 1. And every time when DZY pours a chemical, if there are already one or more chemicals
in the test tube that can react with it, the danger of the test tube will be multiplied by 2. Otherwise the danger remains as it is.

Find the maximum possible danger after pouring all the chemicals one by one in optimal order.

Input

The first line contains two space-separated integers n and m .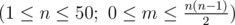

Each of the next m lines contains two space-separated integers xi and yi (1 ≤ xi < yi ≤ n).
These integers mean that the chemical xi will
react with the chemical yi.
Each pair of chemicals will appear at most once in the input.

Consider all the chemicals numbered from 1 to n in some order.

Output

Print a single integer — the maximum possible danger.

Sample test(s)

input

1 0

output

1

input

2 1
1 2

output

2

input

3 2
1 2
2 3

output

4

Note

In the first sample, there's only one way to pour, and the danger won't increase.

In the second sample, no matter we pour the 1st chemical first, or pour the 2nd
chemical first, the answer is always 2.

In the third sample, there are four ways to achieve the maximum possible danger: 2-1-3, 2-3-1, 1-2-3 and 3-2-1 (that is the numbers of the chemicals in order of pouring).

代码例如以下：

#include <cstdio>
#include <cmath>
int father[1005];
int find(int x)
{
    return x==father[x]?x:father[x]=find(father[x]);
}
void Union(int x,int y)
{
    int f1=find(x);
    int f2=find(y);
    if(f1!=f2)
    {
        father[f2]=f1;
    }
}
int main()
{
    int n,m,a,b;
    int i, j;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        for(i = 1 ; i <=n ; i++ )
            father[i] = i ;
        if(m == 0)
        {
            printf("1\n");
            continue;
        }
        int k=0;
        for(i = 0 ; i < m ; i++ )
        {
            scanf("%d%d",&a,&b);
            Union(a,b);
        }
        __int64 msum = 1;
        for(i=1 ; i <= n ; i++)
            if(father[i]==i)
                k++;
			int ans = n - k;
			msum = pow(2,ans);
            printf("%I64d\n",msum);
    }
    return 0 ;
}