【matlab】 拉格朗日插值

第一个函数  "lagrange1.m"

输入:X Y 与点x0

输出:插值函数对应函数值 y0

function y = lagrange1(X,Y,x0)
n = length(X);
m = length(x0);
for i = :m
    z = x0(i);
    s = 0.0;
    for k = :n;
        p = 1.0;
        for j = :n
            if j~=k
                p = p*(z - X(j))/(X(k)-X(j));
            end
        end
        s = p * Y(k) + s;
    end
    y(i) = s;
end

第二个函数  "lagrange2.m"

输入:X Y

输出:插值函数

function L = lagrange2(x,y)
m = length(x);
for k = :m;
    V = ;
    for i = :m;
        if k~=i
            V = conv(V,poly(x(i)))/(x(k)-x(i));
        end
    end
    l(k,:) = poly2sym(V);
end
L = y * l;

"main.m"

一个简单的测试：

x = [1,1.2,1.8,2.5,4];
y =[0.8415,0.9320,0.9738,0.5985,-0.7568];
x0 = [1.6,3];
y0 = lagrange1(x,y,x0)

xx = 0:0.1:5;
yy1 = sin(xx);
yy2 = lagrange1(x,y,xx)
legend('插值','sinx')
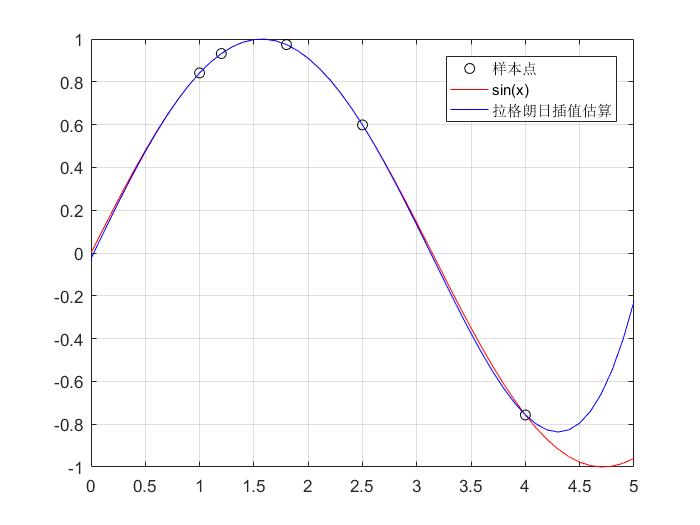
plot(x,y,'ok',xx,yy1,'-r',xx,yy2,'-b');
legend('样本点','sin(x)','拉格朗日插值估算');

hold on;
grid on;
L = lagrange2(x,y);
vpa(L,5)
xx0 = 1:5;
yy0 = lagrange1(x,y,xx0);
yy1 = sin(xx0);
ep = yy1 - yy0