SCP-bzoj-1084

项目编号：bzoj-1084

项目等级：Safe

项目描述：

　　戳这里

特殊收容措施：

　　分类讨论+DP。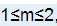#滑稽

　　预处理前缀和s[i][s]=Σa[j][s](∀j∈[1,i])（m=1时略去第二维）

　　对于m=1，设计状态f[i][j]表示前i列中已选取j个矩形的最大分值。转移方程f[i][j]=max(f[i-1][j-1],max{f[k][j-1]+s[i]-s[k-1]})。

　　对于m=2，设计状态f[i][j][k]表示第一行前i列中、第二行前j列中已选取k个矩形的最大分值。有三种转移方式：

　　•传递性转移：max(f[i-1][j][k],f[i][j-1][k])->f[i][j][k]

　　•单行转移：max(max{f[x][j][k-1]+s[i][0]-s[x-1][0]},max{f[i][x][k]+s[j][1]-s[x-1][1]})->f[i][j][k]

　　•双行转移（前提：i=j）：max{f[x][x][k-1]+s[i][0]-s[x-1][0]+s[j][1]-s[x-1][1]}->f[i][j][k]

　　复杂度O(n⁴)。

附录：

 #include <bits/stdc++.h>
 #define range(i,c,o) for(register int i=(c);i<(o);++i)
 #define dange(i,c,o) for(register int i=(c);i>(o);--i)
 using namespace std;

 //#define __debug
 #ifdef __debug
     #define def(t) t
 #else
     #define def(t) __attribute__((optimize("-O2"))) inline t
 #endif

 // quick_io BEGIN HERE
 def(int) getI()
 {
     char c=getchar(); int r=; short s=;
     for(;!isdigit(c)&&c!='-';c=getchar());
     for(;c=='-';c=getchar()) s*=-;
     for(;isdigit(c);c=getchar()) r=(r<<)+(r<<)+c-'';
     return s*r;
 }
 // quick_io END HERE

 static int N=getI(),M=getI(),K=getI();
 int s[][],a[][],f[][][];
 def(int) solve1()
 {
     range(i,,N+) s[i][]=s[i-][]+a[i][];
     bool cur=;
     range(k,,K)
     {
         cur^=;
         range(i,,N+)
         {
             f[i][][cur]=f[i-][][cur];
             range(j,,i) f[i][][cur]=max(
                 f[i][][cur],
                 f[j][][cur^]+s[i][]-s[j][]
             );
         }
     }
     return f[N][][cur];
 }
 def(int) solve2()
 {
     range(i,,N+) range(j,,) s[i][j]=s[i-][j]+a[i][j];
     bool cur=;
     range(k,,K)
     {
         cur^=;
         range(i,,N+) range(j,,N+)
         {
             f[i][j][cur]=max(f[i-][j][cur],f[i][j-][cur]);
             range(x,,i) f[i][j][cur]=max(
                 f[i][j][cur],f[x][j][cur^]+s[i][]-s[x][]
             );
             range(x,,j) f[i][j][cur]=max(
                 f[i][j][cur],f[i][x][cur^]+s[j][]-s[x][]
             );
             if(i==j) range(x,,i) f[i][j][cur]=max(
                 f[i][j][cur],
                 f[x][x][cur^]+s[i][]-s[x][]+s[j][]-s[x][]
             );
         }
     }
     return f[N][N][cur];
 }

 int main()
 {
     range(i,,N+) range(j,,M) a[i][j]=getI();
     return printf("%d\n",M&?solve1():solve2()),;
 }