qbzt day2 晚上(竟然还有晚上)
内容提要
搜索
拓展欧几里得
逆元
先是搜索
A*
有几个数组
g 当前点到根节点的深度
h 当前点到终点理想的最优情况需要走几步
f f=g+h
A*就是把所有的f从小到大排序
启发式搜索相较于其他的搜索的优势在于引入了一个启发式函数f(x) = g(x) +h(x)
g*(x) : 从 S 到 x 的理论最近距离
g(x) : 对 S 到 x 对于 g*(x) 的估计
f*(x) : 从 x 到 T 的理论最近距离,F*(x)=g*(x)+h*(x)
f(x) : 从 x 到 T 对于 f*(x) 的估计,F(x)=g(x)+h(x)
可以理解为:带*的是开挂的,不带*的是真实的
当满足 f(x) <= f*(x) 时,总能找到最优解
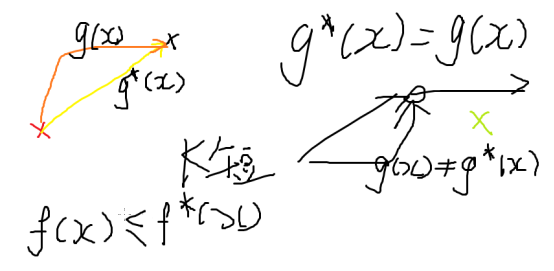
和 BFS 几乎一样,只是每次都弹出当前局面中f(x)最小的那个局面进行扩展
——故需要维护一个优先队列(小根堆)
——使用系统的priority_queue<>即可
当 f(x) = g(x) + h(x) 中 h(x) = 0 即失去了启发式函数,则变为Breath First Search
当 f(x) = g(x) + h(x) 中 g(x) = 0 则变为 Best First Search
当第一次到终点的时候就输出g(x)就可以了
例题:八数码
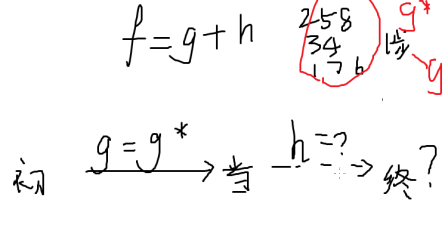
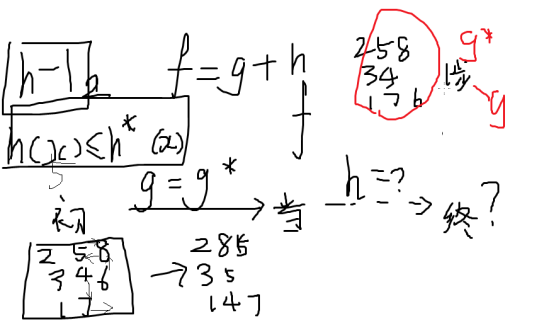
如何告诉计算机某种情况已经到达过呢:
如何做到将一个 1~n 的排列与一个整数做一一对应?
或者更直白的:
如何求出字典序第 k 的排列?
如何求出一个排列在字典序中排第几?

这样数组只需要开9!=36880
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <queue>
const int sizeofpoint=;
const int sizeofedge=; int N, M;
int S, T, K;
int d[sizeofpoint], t[sizeofpoint]; struct node
{
int u; int g; inline node(int _u, int _g):u(_u), g(_g) {}
};
inline bool operator > (const node & , const node & ); struct edge
{
int point; int dist;
edge * next;
};
inline edge * newedge(int, int, edge * );
inline void link(int, int, int);
edge memory[sizeofedge], * port=memory;
edge * e[sizeofpoint], * f[sizeofpoint];
std::priority_queue<node, std::vector<node>, std::greater<node> > h; inline int getint();
inline void dijkstra(int);
inline int Astar(); int main()
{
N=getint(), M=getint();
for (int i=;i<=M;i++)
{
int u=getint(), v=getint(), d=getint();
link(u, v, d);
}
S=getint(), T=getint(), K=getint();
dijkstra(T); if (d[S]==-)
{
puts("-1");
return ;
} K+=S==T; printf("%d\n", Astar()); return ;
} inline bool operator > (const node & u, const node & v)
{
return (u.g+d[u.u])>(v.g+d[v.u]);
} inline edge * newedge(int point, int dist, edge * next)
{
edge * ret=port++;
ret->point=point, ret->dist=dist, ret->next=next;
return ret;
}
inline void link(int u, int v, int d)
{
e[v]=newedge(u, d, e[v]);
f[u]=newedge(v, d, f[u]);
} inline int getint()
{
register int num=;
register char ch;
do ch=getchar(); while (ch<'' || ch>'');
do num=num*+ch-'', ch=getchar(); while (ch>='' && ch<='');
return num;
}
inline void dijkstra(int S)
{
static int q[sizeofedge];
static bool b[sizeofpoint];
int l=, r=; memset(d, 0xFF, sizeof(d)), d[S]=;
for (q[r++]=S, b[S]=true;l<r;l++)
{
int u=q[l]; b[u]=false;
for (edge * i=e[u];i;i=i->next) if (d[i->point]==- || d[u]+i->dist<d[i->point])
{
d[i->point]=d[u]+i->dist;
if (!b[i->point])
{
b[i->point]=true;
q[r++]=i->point;
}
}
}
}
inline int Astar()
{
h.push(node(S, ));
while (!h.empty())
{
node p=h.top(); h.pop();
++t[p.u];
if (p.u==T && t[T]==K)
return p.g;
if (t[p.u]>K)
continue;
for (edge * i=f[p.u];i;i=i->next)
h.push(node(i->point, p.g+i->dist));
}
return -;
}
IDA*
g:从根节点往下几步
h:步数
g+h>d return
双向A*?双向IDA*?
h(x)>h*(x)?
事实上h(x)与h*(x)的关系隐形决定了A*的运行速度与准确度
h(x)越接近h*(x)跑得越快
拓展欧几里得
裴蜀定理:(x, y) = d ===> 存在无限多组整数 a,b:ax + by = d
证明:计算机竞赛不需要证明
扩展欧几里得算法可以帮助我们计算出 (x, y) = d 时一组 a,b:

什么?你问为什么?这么短的代码你背下来不就好了嘛?
扩展欧几里得算法有什么用呢?——计算逆元
逆元的定义:如果 x 对 p 有一个逆元 y,则 x * y == 1 (mod p)
x 对一个数 p 有逆元当且仅当 (x, p) = 1
意义:在取模意义下做除法
由裴蜀定理:存在 a, b 满足:ax + bp = 1
嗯……,等等,岂不是 ax == 1 (mod p)

计算组合数模p
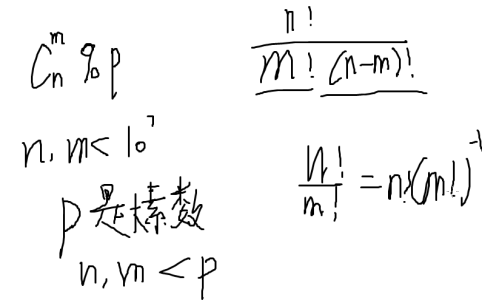
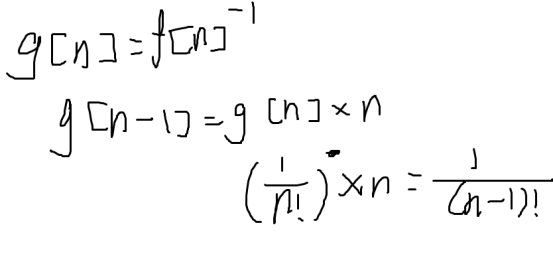

中国剩余定理
问题、求余方程组 x = ai (mod pi)
不多说,背代码:
令 P = p1 * p2 * ... * pn
令 Pi = P / pi
令 Qi = Pi 对 pi 的逆元
则 x = sigma(ai * Pi * Qi)
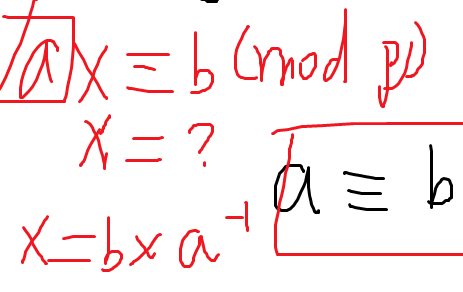
qbzt day2 晚上(竟然还有晚上)的更多相关文章
- qbzt day2 下午
内容提要 高精 矩阵 筛法 先是高精除法 注意细节 高精度开方:神奇的竖式 以小数点为分界线,每两个位砍一刀 87654.321-->08|76|54|.32|1 大概就是先对第一位开方,然后相 ...
- qbzt day2 上午
内容提要 贪心 分治 分块 搜索 接着昨天的讲 过河问题 考虑AB是最快的人,CD是最慢的人,要把CD两个人送过河,只有两种方案,牵扯到四个人,并且n个规模的原问题化成了n-2个规模的子问题 那么最后 ...
- 开发一个 app 有多难?
171 个回答 默认排序 道衍天机 有事情的加微信1293190838找我 1,150 人赞同了该回答 ----------------------------------------------- ...
- Before NOIP 2018
目录 总结 刷题 2018 - 9 - 24 2018 - 9 - 25 2018 - 9 - 26 2018 - 9 - 27 2018 - 9 - 28 2018 - 9 - 29 2018 - ...
- 【扯淡篇】SDOI2018丶一轮游丶记
--某不知名蒟蒻的SDOI2018 R1退役场游记&&OI生涯总结 真的是混不下去了. 进队是不可能的, 进队是不可能进队的. 这辈子不可能进队的. 刷题又不会刷 就是靠打表找规律这种 ...
- 苹果 OS X 系统U盘重装-抹盘重装、系统盘制作
鉴于前段时间系统出了点问题,然后直接将盘抹了,来个彻底干净的系统重装.这里敲下过程.(网络恢复太慢了,我整整一个晚上竟然没down下来,恼怒了,直接U盘装) First,系统盘制作: 1.首先需要有: ...
- 请列出你在从事IT生涯中,最难以忘怀的一次误操作
IT系统最怕什么,我觉得就两点: 1.不可靠的软硬件. 2.误操作. 第一点就不用解释了,第二点是该文的内容,主要摘选自ITPUB的精华贴——[精华] 请列出你在从事DBA生涯中,最难以忘怀的一次误操 ...
- JavaEE——Intellij Idea 创建JavaWeb项目
原文:JavaEE--Intellij Idea 创建JavaWeb项目 折腾Tomcat折腾了两个晚上,第一个晚上怎么都进不了Tomcat的首页,第二个晚上进去了,但是新建的Web项目,在浏览器中运 ...
- 一个想法照进现实-《IT连》创业项目:三天的风投对接活动内幕分享
前言: 话说出来创业的,都有一颗寻找风投的心,只因都有一个共同的特征:缺钱. 有的只是缺几十万,有的缺几百万,有的缺几千万,有的缺几个亿. 中国的市场,只要有需求,就有服务,只要有服务,就多了套路. ...
随机推荐
- 搜索专题: HDU1027Ignatius and the Princess II
Ignatius and the Princess II Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K ( ...
- 原生ajax与伪ajax
原生ajax源码 function GetXHR(){ var xhr = null; if(XMLHttpRequest){ xhr = new XMLHttpRequest(); #如果没有XML ...
- 完整ASP.Net Excel导入
//把EXCEL文件上传到服务器并返回文件路径 private String typename(FileUpload fileloads) { str ...
- 如何获取图片的base64编码
1.准备一张图片,比如1.gif 2.使用chrome浏览器,新建立一个窗口,然后将a.png拖动至浏览器窗口里面,打开控制台(检查),最后点击source 3.使用方法: 注意source获取的一串 ...
- nginx配置反向代理,解决前端开发的跨域问题
适用:开发和生产环境 配置如下 server { listen 10901; server_name res.pre.ices.red; #charset koi8-r; #access_log lo ...
- lsattr - 显示文件在Linux第二扩展文件系统上的特有属性
SYNOPSIS(总览) lsattr [ -RVadv ] [ files... ] DESCRIPTION(描述) lsattr 显示文件在Linux第二扩展文件系统上的特有属性 OPTIONS( ...
- Cookie、Session和Django分页
cookie Cookie的由来 大家都知道HTTP协议是无状态的. 无状态的意思是每次请求都是独立的,它的执行情况和结果与前面的请求和之后的请求都无直接关系,它不会受前面的请求响应情况直接影响,也不 ...
- 为docker配置国内镜像加速器
docker官方镜像仓库地址为:https://hub.docker.com/search?q=&type=image 因为是国外地址,因此下载镜像时速度很慢. 我们需要配置国内镜像加速, 可 ...
- 长沙理工大学第十二届ACM大赛-重现赛I 主持人的烦恼 (sort)
链接:https://ac.nowcoder.com/acm/contest/1/I 来源:牛客网 主持人的烦恼 时间限制:C/C++ 1秒,其他语言2秒 空间限制:C/C++ 131072K,其他语 ...
- oracle汇编01
1: / define numeric label "1"one: / define symbolic label "one"/ ... assembler c ...
