机器学习：1.K近邻算法

1.简单案例：预测男女，根据身高，体重，鞋码

import numpy as np

import matplotlib

import sklearn

from skleran.neighbors import KNeighboorsClassifier

x_train = [[185,80,43],[170,70,41],[163,45,36],[165,60,40],[165,55,37]] # 身高，体重，鞋码

y_train = ["男","男","女","男","女"]

Test_data = [[182,75,41],[159,46,37]]  # 测试数据

knn.predict(Test_data)

array(['男', '女'], dtype='<U1')  # 预测结果

2.图片分类

import sklearn.datasets as datasets 
from sklearn.neighbors import KNeighborsClassifier # KN分类器
# 1.获取数据当做训练样本iris = datasets.load_iris() # 蓝蝴蝶

iris

# {'data': array([[5.1, 3.5, 1.4, 0.2],

        [4.9, 3. , 1.4, 0.2],   # 这里说明一下：data是一个二维数组， data=[[1,2,3],[4,5,6],[7,8,9],......,[n,n+1，n+2]] 假设要找到1,

        [4.7, 3.2, 1.3, 0.2],　　　必须经过两个维度，第一个是外层维度，data[0],第二个是内层维度data[0][0]，就可以找到1。a = [1,2,3] a的下标

        [4.6, 3.1, 1.5, 0.2],　　　只在一个方向变化，a[0],a[1],a[2]; b = [[1,2,3],[4,5,6]] b的下标在两个方向变化。b[0]][1],b[0][2]。

        [5. , 3.6, 1.4, 0.2],

        [5.4, 3.9, 1.7, 0.4],

        [4.6, 3.4, 1.4, 0.3],

        [5. , 3.4, 1.5, 0.2],　　　

        [4.4, 2.9, 1.4, 0.2],

        [4.9, 3.1, 1.5, 0.1],

        [5.4, 3.7, 1.5, 0.2],

        [4.8, 3.4, 1.6, 0.2],

        [4.8, 3. , 1.4, 0.1],

        [4.3, 3. , 1.1, 0.1],

        [5.8, 4. , 1.2, 0.2],

        [5.7, 4.4, 1.5, 0.4],

        [5.4, 3.9, 1.3, 0.4],

        [5.1, 3.5, 1.4, 0.3],

        [5.7, 3.8, 1.7, 0.3],

        [5.1, 3.8, 1.5, 0.3],

        [5.4, 3.4, 1.7, 0.2],

        [5.1, 3.7, 1.5, 0.4],

        [4.6, 3.6, 1. , 0.2],

        [5.1, 3.3, 1.7, 0.5],

        [4.8, 3.4, 1.9, 0.2],

        [5. , 3. , 1.6, 0.2],

        [5. , 3.4, 1.6, 0.4],

        [5.2, 3.5, 1.5, 0.2],

        [5.2, 3.4, 1.4, 0.2],

        [4.7, 3.2, 1.6, 0.2],

        [4.8, 3.1, 1.6, 0.2],

        [5.4, 3.4, 1.5, 0.4],

        [5.2, 4.1, 1.5, 0.1],

        [5.5, 4.2, 1.4, 0.2],

        [4.9, 3.1, 1.5, 0.2],

        [5. , 3.2, 1.2, 0.2],

        [5.5, 3.5, 1.3, 0.2],

        [4.9, 3.6, 1.4, 0.1],

        [4.4, 3. , 1.3, 0.2],

        [5.1, 3.4, 1.5, 0.2],

        [5. , 3.5, 1.3, 0.3],

        [4.5, 2.3, 1.3, 0.3],

        [4.4, 3.2, 1.3, 0.2],

        [5. , 3.5, 1.6, 0.6],

        [5.1, 3.8, 1.9, 0.4],

        [4.8, 3. , 1.4, 0.3],

        [5.1, 3.8, 1.6, 0.2],

        [4.6, 3.2, 1.4, 0.2],

        [5.3, 3.7, 1.5, 0.2],

        [5. , 3.3, 1.4, 0.2],

        [7. , 3.2, 4.7, 1.4],

        [6.4, 3.2, 4.5, 1.5],

        [6.9, 3.1, 4.9, 1.5],

        [5.5, 2.3, 4. , 1.3],

        [6.5, 2.8, 4.6, 1.5],

        [5.7, 2.8, 4.5, 1.3],

        [6.3, 3.3, 4.7, 1.6],

        [4.9, 2.4, 3.3, 1. ],

        [6.6, 2.9, 4.6, 1.3],

        [5.2, 2.7, 3.9, 1.4],

        [5. , 2. , 3.5, 1. ],

        [5.9, 3. , 4.2, 1.5],

        [6. , 2.2, 4. , 1. ],

        [6.1, 2.9, 4.7, 1.4],

        [5.6, 2.9, 3.6, 1.3],

        [6.7, 3.1, 4.4, 1.4],

        [5.6, 3. , 4.5, 1.5],

        [5.8, 2.7, 4.1, 1. ],

        [6.2, 2.2, 4.5, 1.5],

        [5.6, 2.5, 3.9, 1.1],

        [5.9, 3.2, 4.8, 1.8],

        [6.1, 2.8, 4. , 1.3],

        [6.3, 2.5, 4.9, 1.5],

        [6.1, 2.8, 4.7, 1.2],

        [6.4, 2.9, 4.3, 1.3],

        [6.6, 3. , 4.4, 1.4],

        [6.8, 2.8, 4.8, 1.4],

        [6.7, 3. , 5. , 1.7],

        [6. , 2.9, 4.5, 1.5],

        [5.7, 2.6, 3.5, 1. ],

        [5.5, 2.4, 3.8, 1.1],

        [5.5, 2.4, 3.7, 1. ],

        [5.8, 2.7, 3.9, 1.2],

        [6. , 2.7, 5.1, 1.6],

        [5.4, 3. , 4.5, 1.5],

        [6. , 3.4, 4.5, 1.6],

        [6.7, 3.1, 4.7, 1.5],

        [6.3, 2.3, 4.4, 1.3],

        [5.6, 3. , 4.1, 1.3],

        [5.5, 2.5, 4. , 1.3],

        [5.5, 2.6, 4.4, 1.2],

        [6.1, 3. , 4.6, 1.4],

        [5.8, 2.6, 4. , 1.2],

        [5. , 2.3, 3.3, 1. ],

        [5.6, 2.7, 4.2, 1.3],

        [5.7, 3. , 4.2, 1.2],

        [5.7, 2.9, 4.2, 1.3],

        [6.2, 2.9, 4.3, 1.3],

        [5.1, 2.5, 3. , 1.1],

        [5.7, 2.8, 4.1, 1.3],

        [6.3, 3.3, 6. , 2.5],

        [5.8, 2.7, 5.1, 1.9],

        [7.1, 3. , 5.9, 2.1],

        [6.3, 2.9, 5.6, 1.8],

        [6.5, 3. , 5.8, 2.2],

        [7.6, 3. , 6.6, 2.1],

        [4.9, 2.5, 4.5, 1.7],

        [7.3, 2.9, 6.3, 1.8],

        [6.7, 2.5, 5.8, 1.8],

        [7.2, 3.6, 6.1, 2.5],

        [6.5, 3.2, 5.1, 2. ],

        [6.4, 2.7, 5.3, 1.9],

        [6.8, 3. , 5.5, 2.1],

        [5.7, 2.5, 5. , 2. ],

        [5.8, 2.8, 5.1, 2.4],

        [6.4, 3.2, 5.3, 2.3],

        [6.5, 3. , 5.5, 1.8],

        [7.7, 3.8, 6.7, 2.2],

        [7.7, 2.6, 6.9, 2.3],

        [6. , 2.2, 5. , 1.5],

        [6.9, 3.2, 5.7, 2.3],

        [5.6, 2.8, 4.9, 2. ],

        [7.7, 2.8, 6.7, 2. ],

        [6.3, 2.7, 4.9, 1.8],

        [6.7, 3.3, 5.7, 2.1],

        [7.2, 3.2, 6. , 1.8],

        [6.2, 2.8, 4.8, 1.8],

        [6.1, 3. , 4.9, 1.8],

        [6.4, 2.8, 5.6, 2.1],

        [7.2, 3. , 5.8, 1.6],

        [7.4, 2.8, 6.1, 1.9],

        [7.9, 3.8, 6.4, 2. ],

        [6.4, 2.8, 5.6, 2.2],

        [6.3, 2.8, 5.1, 1.5],

        [6.1, 2.6, 5.6, 1.4],

        [7.7, 3. , 6.1, 2.3],

        [6.3, 3.4, 5.6, 2.4],

        [6.4, 3.1, 5.5, 1.8],

        [6. , 3. , 4.8, 1.8],

        [6.9, 3.1, 5.4, 2.1],

        [6.7, 3.1, 5.6, 2.4],

        [6.9, 3.1, 5.1, 2.3],

        [5.8, 2.7, 5.1, 1.9],

        [6.8, 3.2, 5.9, 2.3],

        [6.7, 3.3, 5.7, 2.5],

        [6.7, 3. , 5.2, 2.3],

        [6.3, 2.5, 5. , 1.9],

        [6.5, 3. , 5.2, 2. ],

        [6.2, 3.4, 5.4, 2.3],

        [5.9, 3. , 5.1, 1.8]]),

 'target': array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

        0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]),

 'target_names': array(['setosa', 'versicolor', 'virginica'], dtype='<U10'),



# 训练样本数据

x_train = iris.data[::2]

x_train

# 数组的切割知识点：假设二维数组demo为[[1,0],[2,0],[3,0],[4,0],[5,0],[6,0],[7,0],[8,0],[9,0],[10,0]]

# demo[::2] =[[1,0],[3,0],[5,0],[7,0],[9,0]]] 从头到尾，步长为2进行取值。不改变源数组的结构。

# 训练样本数据

y_train = iris.target[::2]

y_train

# 数组的切割知识点：假设一维数组demo为[1,2,3,4,5,6,7,8，9,10]
# demo[::2] = [1,3,5,7,9]

# 测试样本数据的选取

x_test = iris.data[1::2]

x_test
# 数组的切割知识点：假设二维数组demo为[[1,0],[2,0],[3,0],[4,0],[5,0],[6,0],[7,0],[8,0],[9,0],[10,0]]
# demo[1::2] = [[2, 0], [4, 0], [6, 0], [8, 0], [10, 0]]

# 测试样本对应的真实值

y_test = iris.target[1::2]

y_test
# 同理

# 建立分类实例对象

knn = KNeighborsClassifier()

# 根据训练数据，构建模型

knn.fit(x_train,y_train)

# 根据模型，预测测试数据的值

y_ = knn.predict(x_test)

# 预测值

y_

# array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

       0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, , 1, 1,

       1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

       2, 2, 2, 2, 2, 2, 2, 2, 2])

# 结果值

y_test

# array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,

       0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, , 1, 1,

       1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

       2, 2, 2, 2, 2, 2, 2, 2, 2])

knn.score(x_test,y_test)

# 0.9866666666666667

图片分类结果绘图

from matplotlib.colors import ListedColormap

cmap = ListedColormap(["#FF0000","#00FF00","#0000FF"])

import matplotlib.pyplot as plt

%matplotlib inline

plt.scatter(iris.data[:,2],iris.data[:,3],c=iris.target,cmap=cmap)

# scatter（）详细参数解释：https://blog.csdn.net/anneqiqi/article/details/64125186
# data[:,2] 数组具备的一种切片方法，
# import numpy as np
# demo_ = np.array([[1,0],[2,0],[3,0],[4,0],[5,0]])
# demo_

array([[1, 0],

       [2, 0],

       [3, 0],

       [4, 0],

       [5, 0]])
# demo_[:,1]  # 从开始都结束，逗号后面表示的是取那一列，组成一个新的数组。实例取索引值为1的列。

array([0, 0, 0, 0, 0])

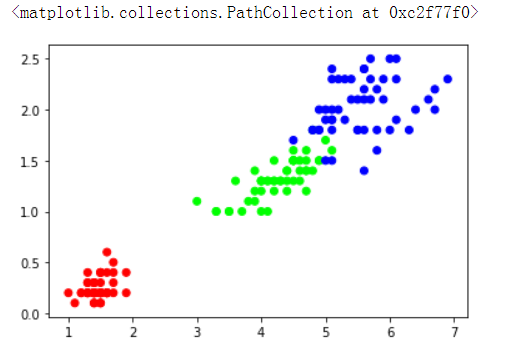
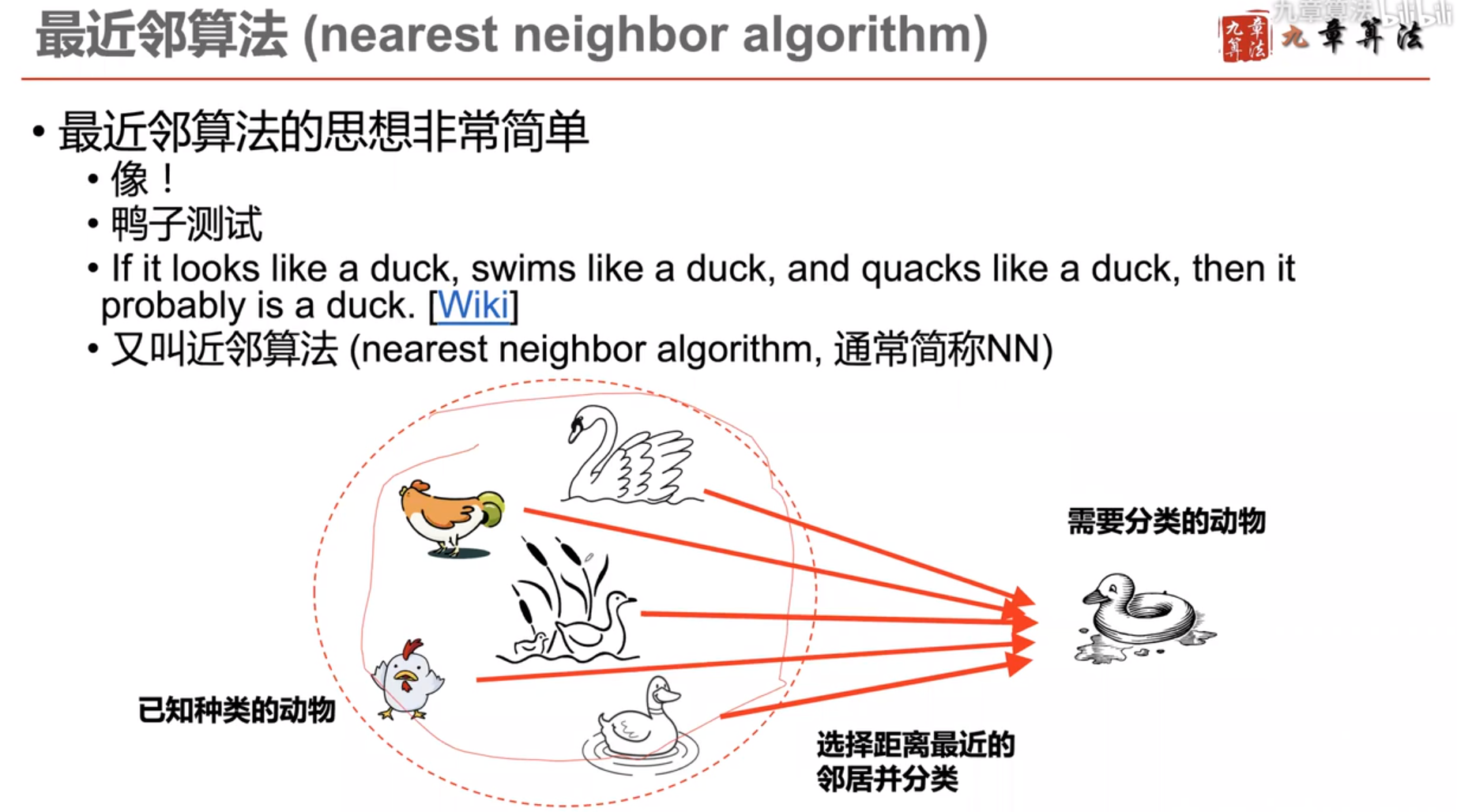
计算机进行分类的依据：像和不像

那么什么叫像，什么叫不像呢？怎么定义呢？

人类是如何判断两个物种像不像的问题？

获取数据集，从哪里来？测量标注

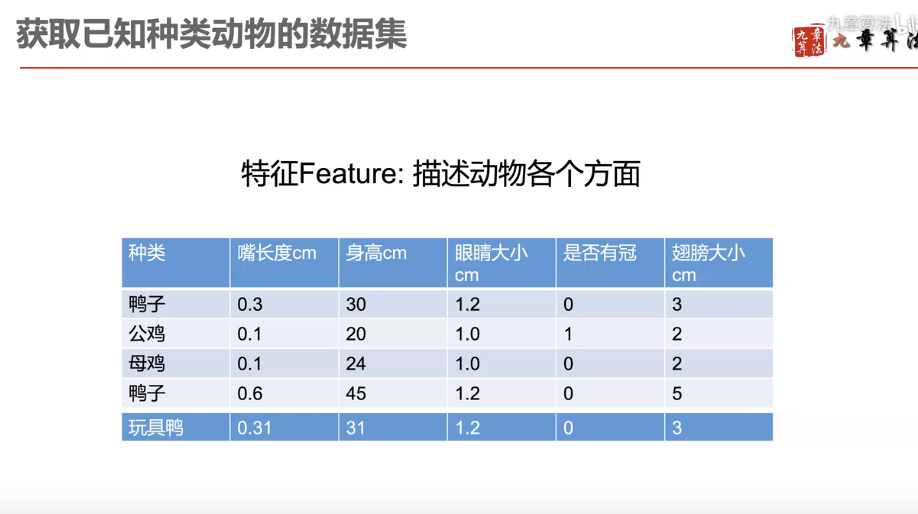
根据已经有的特征值，进行分析，筛选最能代表物种性质的特征

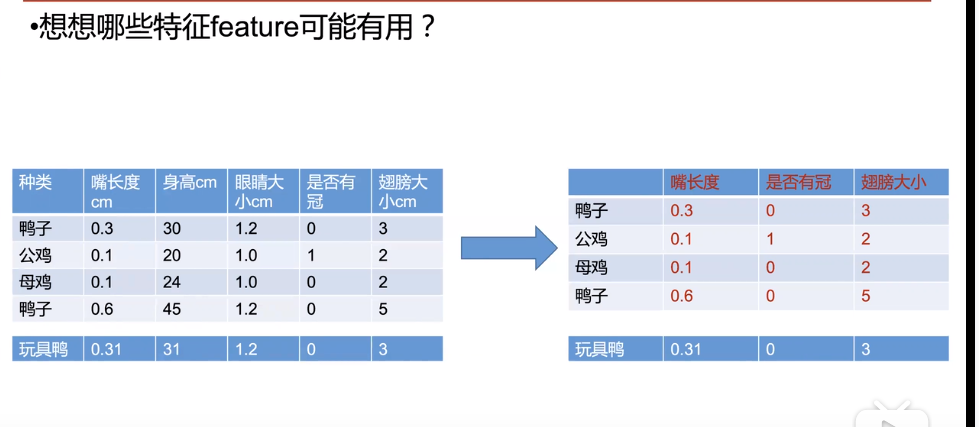
根据特征值，训练模型

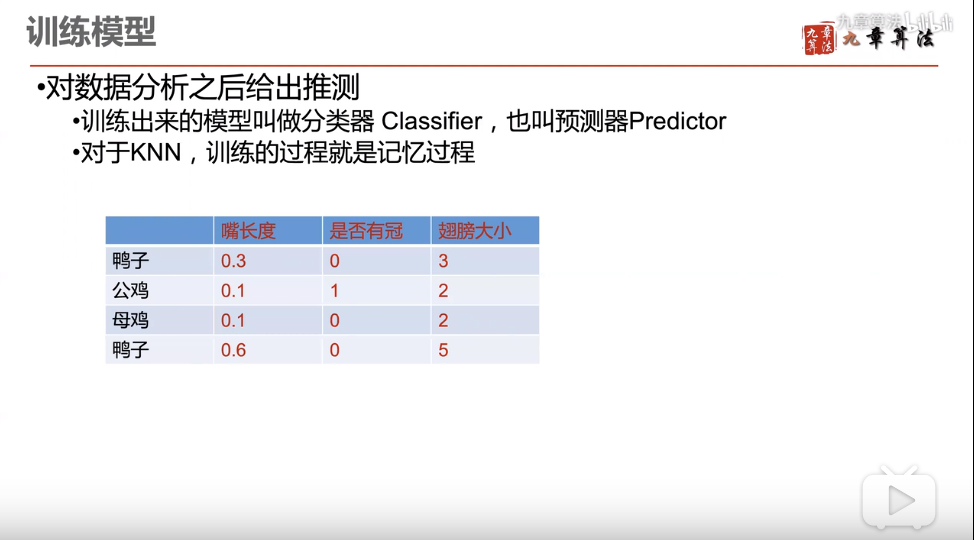
测试

如何在数学上定义两个东西像不像？

向量

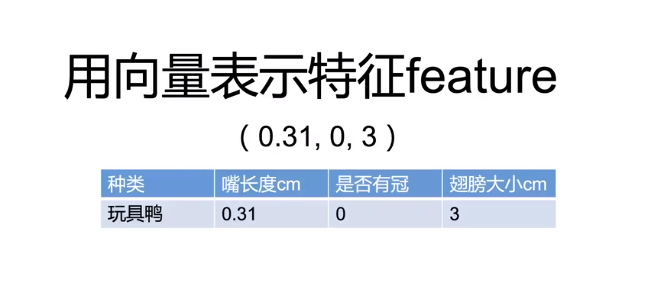
　　图中用向量表示特征值，三维向量，几何意义就是空间中的一个点，x=0.31,y=0,z=0.

　　既然，两个点离得越近，表明特征值越相近，就越像，按照几何解释，那么距离公式是什么呢?

　　两点的距离满足欧几里得距离公式：高维度公式

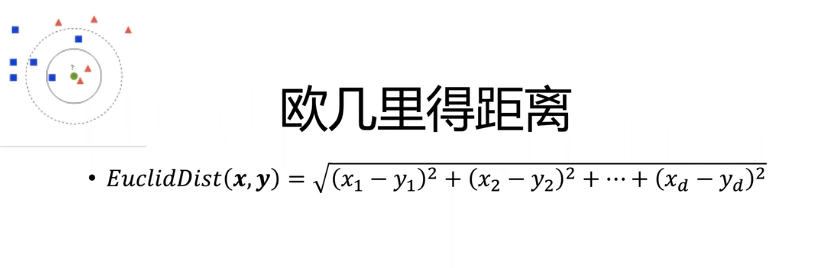
　　机器学习中的数据一般是：{(X1，y1),(X2，y2),(X3，y3),。。。。。,（Xn，yn）}

　　　　其中：X1,X2,X3.....,Xn表示特征值，即向量，y1,y2,y3表示的是标签，即种类。

　　一个新的数据X，求种类，一般做法是，用X的特征向量和已知的数据集中的特征向量，求欧几里得距离，最小的值，新数据X就数据这个数据的标签，就是鸡，鸭，鱼，老虎，狗。

　　误差产生的来源： 误差称为噪音

　　　　1.测量误差：例如鸭子嘴测量的不准确，鸭子眼睛测量的不准确，鸭子翅膀大小测量的不准确。

　　　　2.标注误差：测量数据准确，但是由于标注者没见过这种物种，也分不清是鸡还是鸭。

　　最近邻算法对数据误差非常敏感，数据标错，导致分类错误。

　　KNN K Nearest Neighbor

　　　　怎么解决呢，找一个点容易错误，那我们找最近的k个点，假如最近的三个点，三个点里面的标签分别是，鸡，鸡，鸭，那么我们就认为是鸡，反之是鸭。

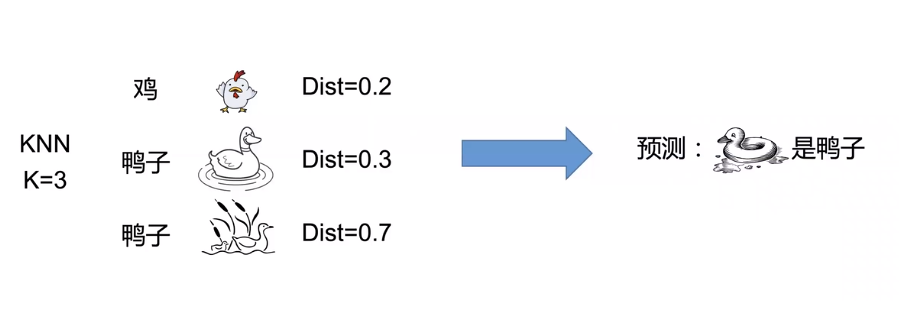
　　训练集和测试集的选择

　　例题

　　为什么28*28的图片表示为矩阵就是28*28*3大小的数值矩阵呢，首先，上图是彩色的图片，图片是由每一个像素组成的，图中共有多少个像素呢，28*28个像素，彩色图片按照rgb表示方式，每一个像素点都是由（0~255的像素值表示）。

　　例如，3*3的图片用矩阵表示就是：

3 * 3像素的图片数组表示为：

img = np.array([[[0,125,255],[0,125,255],[0,125,255]],[[0,125,255],[0,125,255],[0,125,255]],[[0,125,255],[0,125,255],[0,125,255]]])

img

array([[[  0, 125, 255],

        [  0, 125, 255],

        [  0, 125, 255]],

       [[  0, 125, 255],

        [  0, 125, 255],

        [  0, 125, 255]],

       [[  0, 125, 255],

        [  0, 125, 255],

        [  0, 125, 255]]])

1.将rgb值转成灰度值【0,255】

a = [[1],[2],[3],

 [4],[5],[6],

 [7],[8],[9]]

假如认为大于5的值是0，小于5的值是1，那么可以将a数组变化成

a_demo =[[0],[0],[0],
 [0],[1],[1],
 [1],[1],[1]]

　　将一个二维数组转成一个一维数组：a_demo = [0,0,0,1,1,1,1,1] ,但是特征是一个向量，而且是一个一维向量，因此需要转化。

　　2. 数据处理

　　　　将二维数组转成一维数组

　3.缺点分析

　　　特征值也多，模型的个数，为了准确率，数据量也要增多

　4.工作经验

　　5.调参数，找最符合的K值

　　6.流程

分类问题的评价标准

　　混淆矩阵针对二分类

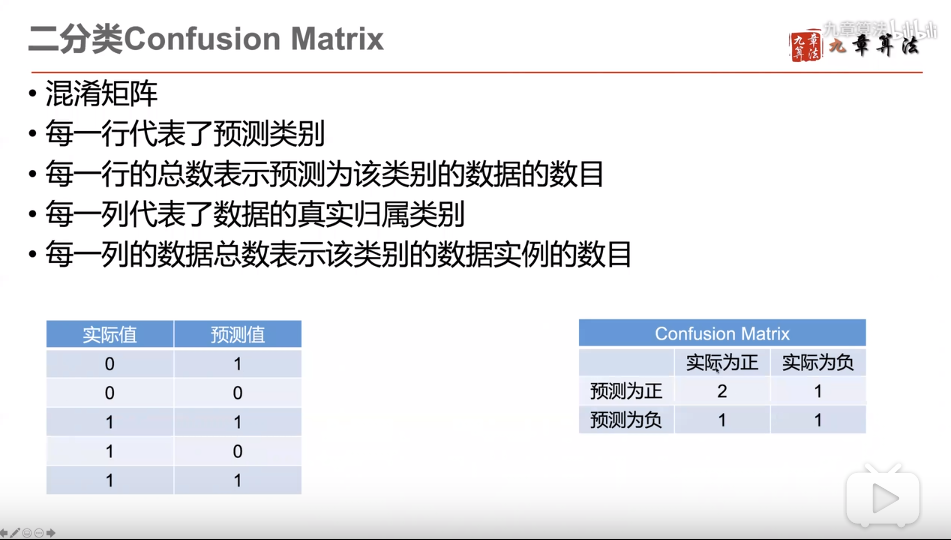
　　评价标准一：精度 Precision

　　评价标准二：召回率 Recall

　　评价标准三：F1-score ：调和 precision和recall的

　　评价标准四：正确率

多分类的方式怎么进行评价？

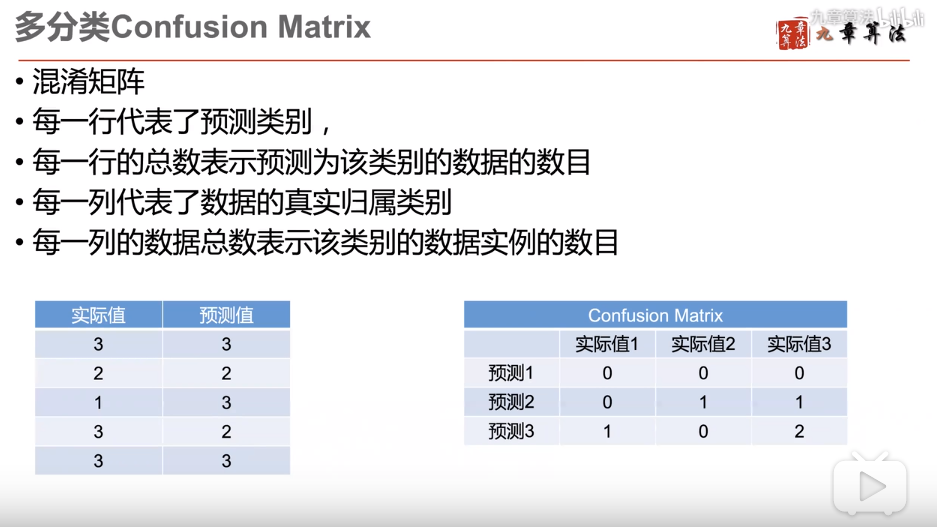
机器学习：1.K近邻算法的更多相关文章

机器学习之K近邻算法（KNN）
机器学习之K近邻算法(KNN) 标签: python 算法 KNN 机械学习苛求真理的欲望让我想要了解算法的本质,于是我开始了机械学习的算法之旅 from numpy import * import ...
【机器学习】k近邻算法（kNN）
一.写在前面本系列是对之前机器学习笔记的一个总结,这里只针对最基础的经典机器学习算法,对其本身的要点进行笔记总结,具体到算法的详细过程可以参见其他参考资料和书籍,这里顺便推荐一下Machine Le ...
第四十六篇入门机器学习——kNN - k近邻算法（k-Nearest Neighbors）
No.1. k-近邻算法的特点 No.2. 准备工作,导入类库,准备测试数据 No.3. 构建训练集 No.4. 简单查看一下训练数据集大概是什么样子,借助散点图 No.5. kNN算法的目的是,假如 ...
机器学习之K近邻算法
K 近邻 (K-nearest neighbor, KNN) 算法直接作用于带标记的样本,属于有监督的算法.它的核心思想基本上就是近朱者赤,近墨者黑. 它与其他分类算法最大的不同是,它是一种&quo ...
机器学习实战-k近邻算法
写在开头,打算耐心啃完机器学习实战这本书,所用版本为2013年6月第1版在P19页的实施kNN算法时,有很多地方不懂,遂仔细研究,记录如下: 字典按值进行排序首先仔细读完kNN算法之后,了解其是用 ...
【机器学习】K近邻算法——多分类问题
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该类输入实例分为这个类. KNN是通过测量不同特征值之间的距离进行分类.它的的思路是:如 ...
机器学习2—K近邻算法学习笔记
Python3.6.3下修改代码中def classify0(inX,dataSet,labels,k)函数的classCount.iteritems()为classCount.items(),另外p ...
机器学习03：K近邻算法
本文来自同步博客. P.S. 不知道怎么显示数学公式以及排版文章.所以如果觉得文章下面格式乱的话请自行跳转到上述链接.后续我将不再对数学公式进行截图,毕竟行内公式截图的话排版会很乱.看原博客地址会有更 ...
[机器学习] k近邻算法
算是机器学习中最简单的算法了,顾名思义是看k个近邻的类别,测试点的类别判断为k近邻里某一类点最多的,少数服从多数,要点摘录: 1. 关键参数:k值 && 距离计算方式 &&am ...
机器学习：k-NN算法（也叫k近邻算法）
一.kNN算法基础 # kNN:k-Nearest Neighboors # 多用于解决分裂问题 1)特点: 是机器学习中唯一一个不需要训练过程的算法,可以别认为是没有模型的算法,也可以认为训练数据集 ...

随机推荐

Hibernate入门学习笔记
1.Hibernate是什么? 2.hibernate怎么配置? 3.SessionFactory是干什么的?有哪些方法经常用? 4.hibernate的现成的增删改查方法怎么使用?都有哪些方法?哪些 ...
Qt5.1 静态编译
下载Qt5.2.1的Qt-every 解压 cd qt-everywhere-opensource-src-5.1.1/ ./configure -prefix 安装目录 -release -sta ...
mariadb（三）查
-查询基本使用(条件,排序,聚合函数,分组,分页) 1)创建一个表结构然后添加数据 create table baba (id int unsigned not null auto_increment ...
SEC7 - MySQL 查询语句--------------进阶3：排序查询
# 进阶3:排序查询 /* 引入: select * from employees; 语法: select 查询列表 from 表 [where 筛选条件] order by 排序的列表 asc/de ...
进程池Pool的简单使用,同步异步的区别
#进程池 """ 当需要创建子进程数量不多的时候,可以直接利用multiprocessing 中的Process动态生成多个进程,但是如果上百甚至上千个任务, " ...
C++ STL map容器值为指针时怎么释放内存
最近在使用STL中map时,遇到了一个问题,就是当map中值为指针对象时怎么释放内存? // 站点与TCP连接映射表 (key为ip_port_stationCode, value为 clientSo ...
jmeter:清除本地指定目录下的所有类型文件
1,创建一个sampler 2,要在本地有一个目录的文件 3,直接上代码 String path = "C:\\临时文件\\test111" ; File file ...
_groovy
_groovy与beanshell类似,只是它执行的是apache groovy脚本,并返回结果. 如果定义了属性 “groovy.utilities”,属性将会被脚本引擎加载,这样就可以定义一些通用 ...
[AGC028D](dp计数)
题解点我 Code #include <bits/stdc++.h> typedef long long LL; typedef unsigned long long uLL; #defi ...
Codeforces 1082D （贪心）
题面传送门分析贪心将度限制大于1的点连成一条链,然后将度限制等于1的点挂上去形状如下图,其中(1,2,3)为度数限制>1的点显然直径长度=(度数限制>1的节点个数)-1+min ...

机器学习：1.K近邻算法

分类问题的评价标准

机器学习：1.K近邻算法的更多相关文章

随机推荐

热门专题