实现 RSA 算法之 C 语言实现（第二章）（老物）

第二章 如何实现应用RSA算法

趁着白天在自家店里的闲暇时间来写写第二章了，假设记住了第一章的各种定理之后，我们又该如何实现RSA密码的加密解密呢？也懒得废话了，直接进入正题吧。

先回顾几个知识点：

1.模运算的性质：

结合律：(a % p * b) % p = (a * b) % p
可知当a == b时，(a % p * a) % p = (a * a) % p

2.欧拉定理

a^φ(n) ≡ 1 (mod n)

3.乘法逆元性质

e * d ≡ 1 (mod n)  => e * d ≡ 1 + k * n(k为任意整数）
注：且当a与n互质时b有解。
注：如何去除带(mod)式子，令k = 0，即忽略其他同余式。

接着我们要证明一种现象，根据欧拉定理与乘法逆元性质外带一点模运算的结合律运算列出如下算式：

M ^ (e * d) = M ^ (1 + k * φ(n)) = M * M ^ (φ(n) * k) ≡ M * (1) ^ k ≡ M (mod n)

由此可知 M ^ (e * d) ≡ M (mod n)

注：M ^ φ(n) ≡ 1 (mod n)（欧拉定理）

基于上述请诸位看以下算式：

C ≡ M ^ e (mod n) ①
M ≡ C ^ d (mod n) ②

于是我们这样做，将①代入②可得：M ≡ M ^ (e * d) (mod n) ，是不是和上述的现象的结果一致呢？

至此我们也可以看出，其实C就是一个中间密文。

那么我们来看看RSA运作流程：

假如A和B两人各自拿着e与d。

首先A要给B解密用的密钥d时必然得满足乘法逆元性质e和n要互质，否则得不到d。

其次对于A要加密一个B可以解开的密文必然满足M < n，否则M不满足②式也就不唯一了，同样B也要满足C < n，否则A也解不对B的数据。

最后利用①与②算式分别生成中间密文交由对方来还原数据。

综上所述，RSA算法描述就到此结束了。

以下是算法实现过程：

一.算法所需参数

1.密文数据规模 n = φ(n)

2.生成两把密钥 e 与 d

二.算法实现代码

一开始想着分C++和C版本代码，后来一想，既然都写了C代码何必浪费时间去写吃力不讨好的C++呢？= -=

于是现在直接给出完整的C代码了，因为第三章想基于第二章的代码部分进行讲解，尤其是一些可以优化本质的代码（即不在语法上改进），说不定出了第二章后就不想写第三章了，所以把代码放出来是为了以后好找理由偷懒吧（“都把代码给你了你怎么还要我来讲解（说笑的= -=）”）

事不宜迟贴代码吧！建议想学习的同学复制后拿到自己的编译器里运行测试一下~

#ifndef RSA
#define RSA
// 欧拉函数：φ(x) = x ∏ (1-1/p)（P是数N的质因数）
int Eular(int n)
{
    int ret = 1, i;
    for(i = 2; i*i <= n; i++)
    {
        if(0 == n%i)
        {
            n /= i, ret *= i-1;
            while(0 == n%i)
                n /= i, ret *= i;
        }
    }
    if(n > 1)
        ret *= n-1;
    return ret;
}
// 欧几里何函数：Gcd(a, b）= Gcd(b, a%b)
int Gcd(int a, int b)
{
    return 0 == b ? a : Gcd(b, a%b);
}
// 拓展欧几里何函数：a*x + b*y = gcd(a, b)
//      gcd(a, b) = gcd(b, a%b)
//    a%b = a-(a/b)*b
//    a*x + b*y = gcd(a, b) = gcd(b, a%b) = b*x1 + (a-(a/b)*b)*y1
//        = b*x1 + a*y1–(a/b)*b*y1
//        = a*y1 + b*(x1–a/b*y1)
int Egcd(int a, int b, int *x, int *y)
{
    int result, t;
    // 递归终止条件
    if (0 == b)
    {
        *x = 1, *y = 0;
        return a;
    }
    result = Egcd(b, a%b, x, y);
    t = *x, *x = *y, *y = t-a/b*(*y);
    return result;
}
// 求解乘法逆元函数 b * (return value) ≡ 1 (mod a)
int Inverse(int a, int b)
{
    int x = 0, y = 0;
    if (Egcd(a, b, &x, &y) != 1)
        return -1;
    // 确保余数与被除数符号一致
    if (b < 0)
        a = -a;
    if ((y %= a) <= 0)
        y += a;
    return y;
}
// 幂模运算a^b%k
// 通常思维暴力求解版本
unsigned PowMod(unsigned a, unsigned b, unsigned c)
{
    unsigned ans = a;
    while(b--)
        ans *= a;
    return ans % c;
}
// 幂模运算a^b%k
// 递归版本 a ^ b (mod c)
// 模运算结合律：(a * a) mod c =( (a mod c) * a ) mod c
// C 语言表达：((a * b) % p = (a % p * b) % p)
unsigned RecursionPowMod(unsigned a, unsigned b, unsigned c)
{
    return b ? a * RecursionPowMod(a, b - 1, c) % c : 1;
}
// 幂模运算a^b%k
// Montgomery 版本
unsigned FastPowMod(unsigned a, unsigned b, unsigned c)
{
    unsigned ans;
    for (ans = 1; b; a = a*a%c, b >>= 1)
        if (b & 1)
            ans = ans*a%c;// LSB位为 1
    return ans;
}
#endif // RSA

#include "stdio.h"
#include "stdlib.h"
int main()
{
    // N 数据规模， En = φ(N)（欧拉函数结果）， Encrypt 与 Decrypt 分别为两把密钥
    int N = 0x1F, En = Eular(N), Encrypt = 2, Decrypt;
    // 生成RSA参数
    do
    {
        // 选取 Encrypt 与 En 互质的数
        while(1 != Gcd(En, Encrypt))
            Encrypt++;
        // 求解其乘法逆元，若 Decrypt == -1 则表示 En 与 Encrypt 不互质
        Decrypt = Inverse(En, Encrypt);
    }while(-1 == Decrypt);
    // 预览 RSA 参数
    printf("En:%4d\tE:%4d\tD:%4d\n", En, Encrypt, Decrypt);
    // 功能测试, 若陷入死循环必然是因为没能还原回原数据导致无法进入下一索引(++)，可自行测试大于N的数据规模
    puts("Test Encrypt Key");
    for(int src = 0, goal; src < N; src++)
    {
        printf("src: %4d\t", src);
        goal = RecursionPowMod(src, Encrypt, N);
        printf("goal: %4d\t", goal);
        src = RecursionPowMod(goal, Decrypt, N);
        printf("src: %4d\n", src);
    }
    puts("Test Decrypt Key");
    for(int src = 0, goal; src < N; src++)
    {
        printf("src: %4d\t", src);
        goal = RecursionPowMod(src, Decrypt, N);
        printf("goal: %4d\t", goal);
        src = RecursionPowMod(goal, Encrypt, N);
        printf("src: %4d\n", src);
    }
    return 0;
}

顺便也贴一下运行结果= -=~标题就是我的IDE路径，采用32位mingw编译器

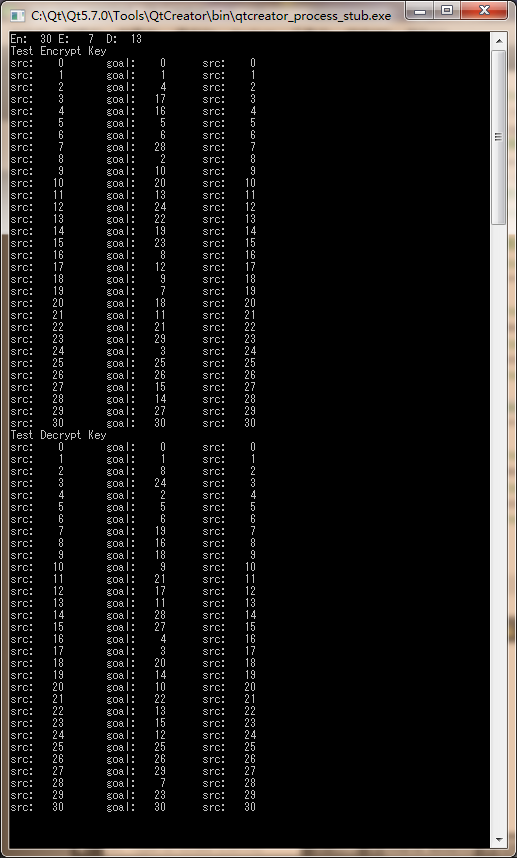
最后的最后，这章也没什么好谈的了，代码说明了一切，看一句代码比废话十句更有效吧我认为~

如果有疑问或想要进一步学习的同学可以私聊我=- = 反正我晚上一直都很有空（偶尔会跑去打魔兽吧~）

现在代码放在我的 Github 了，我翻翻 CryptFunction ，包含 ECC 算法的实现（好像）。