[洛谷P3943]:星空（DP+最短路）

题目传送门

---

题目背景

命运偷走如果只留下结果， 时间偷走初衷只留下了苦衷。
你来过，然后你走后，只留下星空。

---

题目描述

逃不掉的那一天还是来了，小$F$看着夜空发呆。
天上空荡荡的，没有一颗星星——大概是因为天上吹不散的乌云吧。
心里吹不散的乌云，就让它在那里吧，反正也没有机会去改变什么了。
小$C$拿来了一长串星型小灯泡，假装是星星，递给小$F$，想让小$F$开心一点。不过，有着强迫症的小$F$发现，这串一共$n$个灯泡的灯泡串上有$k$个灯泡没有被点亮。小$F$决定和小$C$一起把这个灯泡串全部点亮。
不过，也许是因为过于笨拙，小$F$只能将其中连续一段的灯泡状态给翻转——点亮暗灯泡，熄灭亮灯泡。经过摸索，小$F$发现他一共能够翻转$m$种长度的灯泡段中灯泡的状态。
小$C$和小$F$最终花了很长很长很长很长很长很长的时间把所有灯泡给全部点亮了。他们想知道他们是不是蠢了，因此他们找到了你，让你帮忙算算：在最优的情况下，至少需要几次操作才能把整个灯泡串给点亮？

---

输入格式

从标准输入中读入数据。
输入第$1$行三个正整数$n,k,m$。
输入第$2$行$k$个正整数，第$i$个数表示第$i$个被没点亮的灯泡的位置$a_i$​。
输入第$3$行$m$个正整数，第$i$个数表示第$i$种操作的长度$b_i$​。

---

输出格式

输出标准输入中。
输出一行一个非负整数，表示最少操作次数。

---

样例

样例输入

5 2 2
1 5
3 4

样例输出

2

---

数据范围与提示

样例解释：

数据范围：

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表：

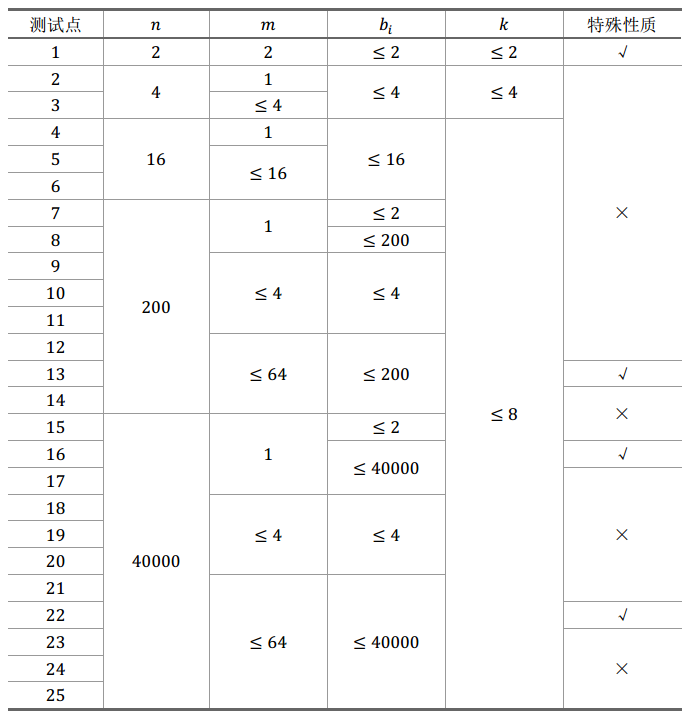
特殊性质：保证答案小于$4$。

---

题解

发现$k$很小。
那么我们考虑转化这个问题，利用状压$DP$。
再想区间修改，离线，那么用差分，也就是异或差分。
问题转化为：
    给定一个长度为$n$的$0/1$串，其中只有不超过$2k$个$0$。
    每次操作是，从给定的$m$种距离中选择一种，选择序列上相距这个距离的两个位同时取反。
    求至少需要操作多少次才能使得整个串全为$1$。
    如果某个地方有$0$，那么这个位置一定会进行操作来消去这个$0$。
    我们假定每次我们都选含$0$的来进行操作：
        一个$1$一个$0$：可以视作移动；
        两个$0$：看作将其中一个$0$移到另一个$0$的位置，随后它们均消去。
发现又可以转化问题：
    给定一个有$n$个点的图，其中之后不超过$2k$个点存在物品。
    每次操作时，从给定的$m$种距离中选择一种，选择序列上一个物品进行移动；两个物品碰到一起会消去。
    求至少需要操作多少次才能使得所有物品消失。
    消去的两个物品可以看作是其中一个移动到了另外一个物品的位置，代价即为从一个物品到另一个物品所需要的最小步数；
    我们发现，这种移动只有$2k$个起点；
    同时，图上$n$个点每个点有$m$条边；
    因此，预处理两两之间所需要的最短步数可以使用$\Theta(n\times m\times k)$的$BFS$
最后一次转化问题：
    有$2k$个物品，选择其中两个消去，分别有不同的代价，求使得所有物品消失的最小代价。
    状压$DP$轻松解决。
时间复杂度：$\Theta(n\times m\times k+k\times 2^{2k})$。
期望得分：$100$分。
实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
int n,k,m;
bool a[40001];
int b[100];
int dis[20][40001];
int dp[300000];
int cnt;
pair<int,int> p[20];
queue<int> q;
void bfs(pair<int,int> x)
{
	dis[x.first][x.second]=0;
	q.push(x.second);
	while(q.size())
	{
		int flag=q.front();
		q.pop();
		for(int i=1;i<=m;i++)
		{
			if(flag-b[i]>=0&&dis[x.first][flag-b[i]]>dis[x.first][flag]+1)
			{
				dis[x.first][flag-b[i]]=dis[x.first][flag]+1;
				q.push(flag-b[i]);
			}
			if(flag+b[i]<=n&&dis[x.first][flag+b[i]]>dis[x.first][flag]+1)
			{
				dis[x.first][flag+b[i]]=dis[x.first][flag]+1;
				q.push(flag+b[i]);
			}
		}
	}
}
int getans(int x)
{
	if(dp[x]!=-1)return dp[x];
	if(!x)return x;
	int res=1<<30;
	int flag=0;
	while(!(x&(1<<flag)))flag++;
	for(int i=flag+1;i<=2*k;i++)
		if(x&(1<<i))res=min(res,getans(x^(1<<flag)^(1<<i))+dis[flag][p[i].second]);
	dp[x]=res;
	return res;
}
int main()
{
	memset(dis,0x3f,sizeof(dis));
	memset(dp,-1,sizeof(dp));
	scanf("%d%d%d",&n,&k,&m);
	for(int i=1;i<=k;i++)
	{
		int x;
		scanf("%d",&x);
		a[x]=1;
	}
	for(int i=1;i<=m;i++)
		scanf("%d",&b[i]);
	for(int i=0;i<=n;i++)
		if(a[i]!=a[i+1])
			p[cnt]=make_pair(cnt++,i);
	for(int i=0;i<cnt;i++)
		bfs(p[i]);
	cout<<getans((1<<cnt)-1);
	return 0;
}

---

rp++