IOS- 堆和栈 详解

Objective-C的对象在内存中是以堆的方式分配空间的,并且堆内存是由你释放的，即release

栈由编译器管理自动释放的，在方法中（函数体）定义的变量通常是在栈内，因此如果你的变量要跨函数的话就需要将其定义为成员变量。

1.栈区(stack):由编译器自动分配释放，存放函数的参数值，局部变量等值。其操作方式类似于数据结构中的栈。

2.堆区(heap):一般由程序员分配释放，若程序员不释放，则可能会引起内存泄漏。注堆和数据结构中的堆栈不一样，其类是与链表。

操作系统iOS 中应用程序使用的计算机内存不是统一分配空间，运行代码使用的空间在三个不同的内存区域，分成三个段：“text segment “，“stack segment ”，“heap segment ”。

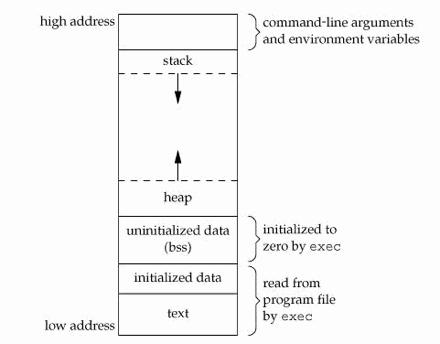
段“text segment ”是应用程序运行时应用程序代码存在的内存段。每一个指令，每一个单个函数、过程、方法和执行代码都存在这个内存段中直到应用程序退出。一般情况下，你不会真的不得不知道这个段的任何事情。

当应用开始以后，函数main() 被调用，一些空间分配在”stack” 中。这是为应用分配的另一个段的内存空间，这是为了函数变量存储需要而 分配的 内存。每一次在应用中调用一个函数，“stack ”的一部分会被分配在”stack” 中，称之为”frame” 。新函数的本地变量分配在这里。

正如名称所示，“stack ”是后进先出（LIFO ）结构。当函数调用其他的函数时，“stack frame ”会被创建；当其他函数退出后，这个“frame ”会自动被破坏。

“heap” 段也称为”data” 段，提供一个保存中介贯穿函数的执行过程，全局和静态变量保存在“heap”中，直到应用退出。

为了访问你创建在heap 中的数据，你最少要求有一个保存在stack 中的指针，因为你的CPU 通过stack 中的指针访问heap 中的数据。

你可以认为stack 中的一个指针仅仅是一个整型变量，保存了heap 中特定内存地址的数据。实际上，它有一点点复杂，但这是它的基本结构。

简而言之，操作系统使用stack 段中的指针值访问heap 段中的对象。如果stack 对象的指针没有了，则heap 中的对象就不能访问。这也是内存泄露的原因。

在iOS 操作系统的stack 段和heap 段中，你都可以创建数据对象。

stack 对象的优点主要有两点，一是创建速度快，二是管理简单，它有严格的生命周期。stack 对象的缺点是它不灵活。创建时长度是多大就一 直是多 大，创建时是哪个函数创建的，它的owner 就一直是它。不像heap 对象那样有多个owner ，其实多个owner 等同于引用计数。只有 heap 对象才是采用“引用计数”方法管理它。

stack 对象的创建

只要栈的剩余空间大于stack 对象申请创建的空间，操作系统就会为程序提供这段内存空间，否则将报异常提示栈溢出。

heap 对象的创建

操作系统对于内存heap 段是采用链表进行管理的。操作系统有一个记录空闲内存地址的链表，当收到程序的申请时，会遍历链表，寻找第一个空间大于所申请的heap 节点，然后将该节点从空闲节点链表中删除，并将该节点的空间分配给程序。

例如：

NSString 的对象就是stack 中的对象，NSMutableString 的对象就是heap 中的对象。前者创建时分配的内存长度固定且不可修改；后者是分配内存长度是可变的，可有多个owner, 适用于计数管理内存管理模式。

两类对象的创建方法也不同，前者直接创建“NSString * str1=@"welcome"; “，而后者需要先分配再初始化“ NSMutableString * mstr1=[[NSMutableString alloc] initWithString:@"welcome"]; ”。