通俗易懂--岭回归(L2)、lasso回归(L1)、ElasticNet讲解(算法+案例)

1.L2正则化(岭回归)

1.1问题

想要理解什么是正则化，首先我们先来了解上图的方程式。当训练的特征和数据很少时，往往会造成欠拟合的情况，对应的是左边的坐标；而我们想要达到的目的往往是中间的坐标，适当的特征和数据用来训练；但往往现实生活中影响结果的因素是很多的，也就是说会有很多个特征值，所以训练模型的时候往往会造成过拟合的情况，如右边的坐标所示。

1.2公式

以图中的公式为例，往往我们得到的模型是：

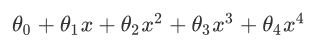
为了能够得到中间坐标的图形，肯定是希望θ3和θ4越小越好，因为这两项越小就越接近于0，就可以得到中间的图形了。

对应的损失函数也加上这个惩罚项(为了惩罚θ)：假设λ=1000

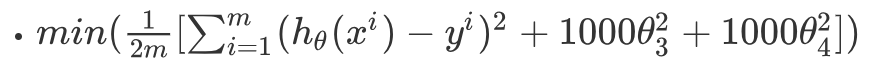
为了求得最小值，使θ值趋近于0，这就达到了我们的目的，得到中间坐标的方程。

把以上公式通用化得：

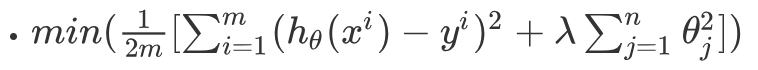
相当于在原始损失函数中加上了一个惩罚项(λ项)

这就是防止过拟合的一个方法，通常叫做L2正则化，也叫作岭回归。

1.3对应图形

我们可以简化L2正则化的方程：

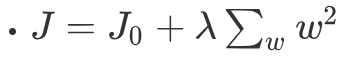
J0表示原始的损失函数，咱们假设正则化项为：

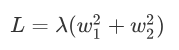
我们不妨回忆一下圆形的方程：

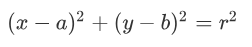
其中(a,b)为圆心坐标，r为半径。那么经过坐标原点的单位元可以写成：

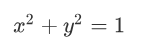
正和L2正则化项一样，同时，机器学习的任务就是要通过一些方法（比如梯度下降）求出损失函数的最小值。

此时我们的任务变成在L约束下求出J0取最小值的解。

求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来。如下图：

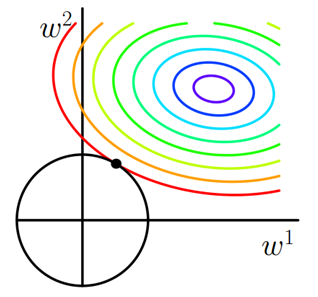
L表示为图中的黑色圆形，随着梯度下降法的不断逼近，与圆第一次产生交点，而这个交点很难出现在坐标轴上。

这就说明了L2正则化不容易得到稀疏矩阵，同时为了求出损失函数的最小值，使得w1和w2无限接近于0，达到防止过拟合的问题。

1.4使用场景

只要数据线性相关，用LinearRegression拟合的不是很好，需要正则化，可以考虑使用岭回归(L2), 如何输入特征的维度很高,而且是稀疏线性关系的话，岭回归就不太合适,考虑使用Lasso回归。

1.5代码实现

GitHub代码--L2正则化

2.L1正则化(lasso回归)

2.1公式

L1正则化与L2正则化的区别在于惩罚项的不同：

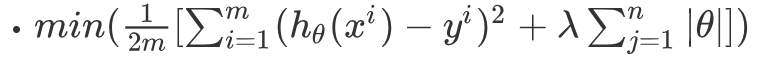
L1正则化表现的是θ的绝对值，变化为上面提到的w1和w2可以表示为：

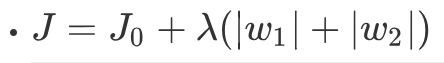
2.2对应图形

求解J0的过程可以画出等值线。同时L1正则化的函数也可以在w1w2的二维平面上画出来。如下图：

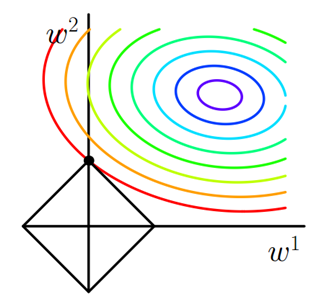
惩罚项表示为图中的黑色棱形，随着梯度下降法的不断逼近，与棱形第一次产生交点，而这个交点很容易出现在坐标轴上。这就说明了L1正则化容易得到稀疏矩阵。

2.3使用场景

L1正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0，从而增强模型的泛化能力。对于高纬的特征数据,尤其是线性关系是稀疏的，就采用L1正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征，那么L1正则化(Lasso回归)更是首选了。

2.4代码实现

GitHub代码--L1正则化

3.ElasticNet回归

3.1公式

ElasticNet综合了L1正则化项和L2正则化项，以下是它的公式：

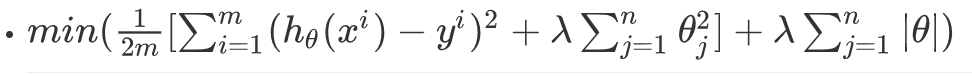
3.2使用场景

ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候，可以考虑使用ElasticNet回归来综合，得到比较好的结果。

3.3代码实现

from sklearn import linear_model
#得到拟合模型，其中x_train,y_train为训练集
ENSTest = linear_model.ElasticNetCV(alphas=[0.0001, 0.0005, 0.001, 0.01, 0.1, 1, 10], l1_ratio=[.01, .1, .5, .9, .99],  max_iter=5000).fit(x_train, y_train)
#利用模型预测，x_test为测试集特征变量
y_prediction = ENSTest.predict(x_test)

欢迎添加微信交流！请备注“机器学习”。