Square Destroyer-POJ 1084 （IDA*）

Description

The left figure below shows a complete 3*3 grid made with 2*(3*4) (=24) matchsticks. The lengths of all matchsticks are one. You can find many squares of different sizes in the grid. The size of a square is the length of its side. In the grid shown in the left figure, there are 9 squares of size one, 4 squares of size two, and 1 square of size three.

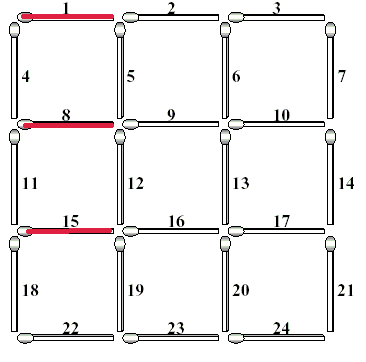
Each matchstick of the complete grid is identified with a unique number which is assigned from left to right and from top to bottom as shown in the left figure. If you take some matchsticks out from the complete grid, then some squares in the grid will be destroyed, which results in an incomplete 3*3 grid. The right figure illustrates an incomplete 3*3 grid after removing three matchsticks numbered with 12, 17 and 23. This removal destroys 5 squares of size one, 3 squares of size two, and 1 square of size three. Consequently, the incomplete grid does not have squares of size three, but still has 4 squares of size one and 1 square of size two.



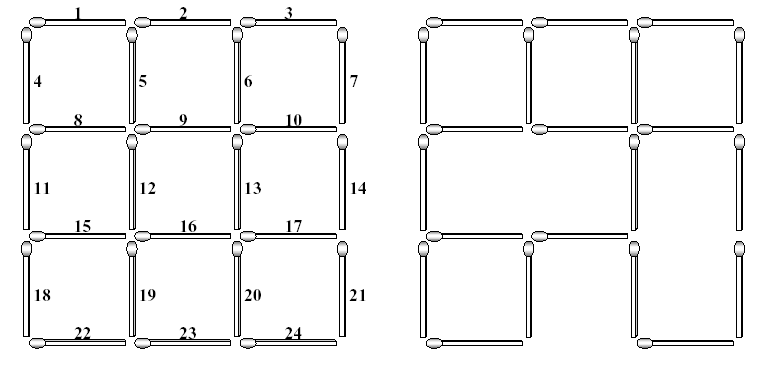
As input, you are given a (complete or incomplete) n*n grid made with no more than 2n(n+1) matchsticks for a natural number 5 <= n . Your task is to compute the minimum number of matchsticks taken

out to destroy all the squares existing in the input n*n grid.

Input

The input consists of T test cases. The number of test cases (T ) is given in the first line of the input file.

Each test case consists of two lines: The first line contains a natural number n , not greater than 5, which implies you are given a (complete or incomplete) n*n grid as input, and the second line begins with a nonnegative integer k , the number of matchsticks that are missing from the complete n*n grid, followed by

k numbers specifying the matchsticks. Note that if k is equal to zero, then the input grid is a complete n*n grid; otherwise, the input grid is an incomplete n*n grid such that the specified k matchsticks are missing from the complete n*n grid.

Output

Print exactly one line for each test case. The line should contain the minimum number of matchsticks that have to be taken out to destroy all the squares in the input grid.

Sample Input

2
2
0
3
3 12 17 23

Sample Output

3
3

题意：t组数据，给出n代表n*n的网格，给一个值k，然后k个值，表示去掉k所代表的边，问还需要最少去掉几条边可以使得网格中没有正方形。

思路:

评估函数：每出现一个正方形，就删去其含有的边，然后继续扫描正方形，这样计数出来的次数比实际需要次数小（因为一次删去了多条边）

对于网格中正方形的枚举：

①先枚举正方形大小，1 <= size <= n;

②枚举网格每行最左边的火柴

③对于每个行位置，枚举该行可以成为该size大小正方形的最左边火柴

④标记该正方形的所有上边界和下边界（知道size和上边界最左火柴很容易求得）

　标记该正方形的所有左边界和有边界

（代码借鉴网上，侵删）

stick【i】表示含有i火柴的正方形编号

square【i】表示i正方形所含火柴编号

 

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;

int t;
int totsquare,totstick,base;
vector<int>stick[],square[];
int n,k;
int ans;
int exi[],tmp[];

int cal()
{
    int res = ;
    for(int i=;i<=totsquare;i++)tmp[i] = exi[i];
    for(int i=;i<=totsquare;i++)if(!tmp[i])
    {
        res++;
        for(int j=;j<square[i].size();j++)
        {
            for(int l=;l<stick[square[i][j]].size();l++)
            {
                tmp[stick[square[i][j]][l]]--;
            }
        }
    }
    return res;
}

bool dfs(int sum,int lim)
{
    if(sum + cal() > lim)return ;
    int tmp = ;
    while(exi[tmp] <  && tmp <= totsquare)tmp++;
    if(tmp > totsquare)
    {
        ans = min(ans,sum);
        return ;
    }
    for(int i=;i<square[tmp].size();i++)
    {
        int sti = square[tmp][i];
        for(int j=;j<stick[sti].size();j++)
        {
            exi[stick[sti][j]]--;
        }
        if(dfs(sum+,lim))return ;
        for(int j=;j<stick[sti].size();j++)
        {
            exi[stick[sti][j]]++;
        }
    }
    return ;
}
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&k);
        totsquare = ,totstick = *n*(n+),base = *n+;
        for(int i=; i<; i++)
        {
            stick[i].clear();
            square[i].clear();
        }
        for(int sz=; sz<=n; sz++)
        {
            for(int i=; (i-)/base+sz<=n; i+=base)
            {
                for(int j=i; j-i+sz<=n; j++)
                {
                    totsquare++;
                    for(int l=j; l-j<sz; l++) // 正方形上下边界标记
                    {
                        square[totsquare].push_back(l);
                        square[totsquare].push_back(l+sz*base);
                        stick[l].push_back(totsquare);
                        stick[l+sz*base].push_back(totsquare);
                    }
                    for(int l=j+n; (l-j-sz)/base<sz; l+=base) //正方形左右边界标记
                    {
                        square[totsquare].push_back(l);
                        square[totsquare].push_back(l+sz);
                        stick[l].push_back(totsquare);
                        stick[l+sz].push_back(totsquare);
                    }
                }
            }
        }
        memset(exi,,sizeof(exi));
        for(int i=; i<=k; i++)
        {
            int t_st;
            scanf("%d",&t_st);
            for(int j=; j<stick[t_st].size(); j++)
            {
                exi[stick[t_st][j]]--;
            }
            totstick--;
        }
        ans = totstick;
        for(int maxd=;; maxd++)
        {
            if(dfs(,maxd))
            {
                printf("%d\n",ans);
                break;
            }
        }
    }
}