特征脸是怎么提取的之主成分分析法PCA

机器学习笔记 多项式回归这一篇中,我们讲到了如何构造新的特征,相当于对样本数据进行升维.

那么相应的,我们肯定有数据的降维.那么现在思考两个问题

• 为什么需要降维
• 为什么可以降维

第一个问题很好理解,假设我们用KNN训练一些样本数据,相比于有1W个特征的样本,肯定是训练有1K个特征的样本速度更快,因为计算量更小嘛.

第二个问题,为什么可以降维.一个样本原先有1W个特征,现在减少到1K个,不管如何变换,数据包含的信息肯定是减少了,这是毫无疑问的.但是信息的减少是否意味着我们对于样本的认知能力的下降？这个则未必.

以minist数据集为例,每一个数字图片都由N个像素构成,即样本有N个特征,但是我们不需要精确地知道每一个像素的值,依然能够分辨出这个数字是几,你可以通俗地理解为,比如你把每张图的边边角角都减掉,并不影响你识别这是几。  由此,我们知道,样本特征的重要性并不是一致的,有的重要,也即所谓的主成分.

现在问题则转换为:我们怎么样寻找到一种方法,使得降维后"重要的特征"尽可能地保留,也即降维后信息的丢失最少?

依然从一个极端的例子入手,假设我们有M个样本,每个样本2个特征,特征1的波动幅度很大,特征2的波动幅度很小.

此时,如果要把这M个样本降成1维,采用最简单粗暴的方式,丢弃一个特征,是丢弃feature1呢还是feature2呢？

如果,丢弃feature1的话,我们的样本就只剩下了feature2，而feature2的值在3附近微小的波动,几乎没有变化.   没有变化,机器学习算法就没法从中学习到足够的信息.比如M个样本对应着M个label，这M个label各不相同.来了个新样本,特征值还是3,这时候我们是没法推算出新样本的label的.

对机器学习算法而言,我们希望在合理的范围内,数据的分布越分散越好,即数据的方差越大越好,这样才能学习到足够多的信息.

而这也正是PCA降维的理论基础:我们希望找到一个新的N维坐标系,使得数据在这个新的N维坐标系的前K个坐标轴上分布,方差最大.这样的N维坐标系中的K个坐标轴就是我们所要寻找的K个主成分.

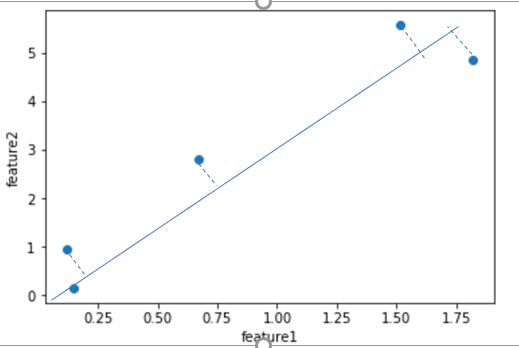
比如对这个图中的蓝色的点而言,我们希望找到一个向量w(图中的蓝色线),使得各点在w上的投影点,方差最大.样本点$X^{(i)}$投影到单位向量w后得到$X_p^{(i)}$，这些新的样本点的方差为$\frac{\sum_{i=1}^m (X_p^{(i)} - \overline X_p)^2)} m$,为了方便计算,在向w投影之前,我们对样本X做demean去均值处理,即每个特征值减去该维度特征的均值,这个操作并不会影响数据的分布.demean后的样本点投影到w后得到的新样本点的方差变为$\frac{\sum_{i=1}^m (X_p^{(i)})^2)} m$.注意这里$X_p^{(i)}$是一个向量.所以我们的方差可以转变为$$Var(X_p) = \frac{\sum_{i=1}^m || X_p^{(i)} ||^2)} m$$

注意，样本点$X^{(i)}$投影到单位向量w后得到$X_p^{(i)}$，由向量点乘的定义我们能够得到$X^{(i)} \cdot w = || X^{(i)}|| \cdot || w|| \cdot \cos \theta =  || X^{(i)}|| \cdot \cos \theta = || X_p^{(i)} ||$.由此我们的目标转变为使得$$Var(X_p) = \frac{\sum_{i=1}^m  X^{(i)} \cdot w^2)} m$$最大化.

接下来我们用梯度上升法求出这个w。现在先不用管梯度上升法是怎么回事,本篇重点在于理解PCA。梯度下降法梯度上升法以后会再写博文解释.这个w也就是我们的第一主成分.即样本投影到这个方向后,方差最大,损失信息最少.那么现在我们如何求出第二主成分呢？

求出这个w之后,注意w是一个N维向量. 我们就可以得到X在w之外剩余的分量为$X^{’(i)}=X^{(i)}-X_p^{(i)}=X^{(i)}-X^{(i) \cdot w}$，对$X^{’(i)}$，我们再次求出一个w2，使得其在w2上的投影的方差最大,求解方法同上.

我们不断循环这个过程,就可以求解出k个w，记做

$$W_k=\begin{bmatrix} W_1^{(1)}& W_2^{(1)}& … &W_n^{(1)} \\ W_1^{(2)}& W_2^{(2)}& … &W_n^{(2)} \\ … \\ W_1^{(k)}& W_2^{(k)}& … &W_n^{(k)} \\ \end{bmatrix}$$.即$$W_k=\begin{bmatrix} w_1\\ w_2 \\ … \\w_k\\ \end{bmatrix}$$

这个$W_k$即我们求出的新的N维坐标系的前K个坐标轴.

原始数据点在新的N维坐标系的第k个坐标轴的投影距离为$X^{(i)} \cdot w_k$,则原始样本在新的N维坐标系的前K个坐标轴上可以表示为$$X^{‘}=XW_k^T$$。这样我们就把矩阵M*N的矩阵X转换成了M*K的矩阵$X^{'}$，从而达到了降维的目的.

---

原理部分说完了,我们来看一下sklearn中的具体api使用.

class sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False, svd_solver=’auto’, tol=0.0, iterated_power=’auto’, random_state=None)[source]¶

常用参数有n_components,代表降维后需要保留的维度数.如果0<n_components<1的话,表示降维后需要保留的方差比例.(你可以通俗地理解为保留的信息占原始信息的百分比)

常用属性：

explained_variance_ : array, shape (n_components,)  解释了新的坐标系中的k个坐标轴的每一个轴所解释的方差.

explained_variance_ratio_ : array, shape (n_components,) 解释了新的坐标系中的k个坐标轴的每一个轴所解释的方差所占百分比.

n_components_:主成分个数.即降到的维度数.

components_ : array, shape (n_components, n_features) 主成分.

这样说显得有点抽象,看个例子你就全明白.

from sklearn.decomposition import PCA
 
pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
 
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)

我们把64维的X_train降成二维的X_train_reduction.

pca.explained_variance_

array([ 175.77007821,  165.73864334])

pca.explained_variance_ratio_

array([ 0.14566817,  0.13735469])

什么意思呢？降维后的X_train_reduction在第一个维度上(第一主成分)的方差为175.77,占比为14.56%.

来看下当我们将n_components传参为原始特征数量时

from sklearn.decomposition import PCA
 
pca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
pca.explained_variance_ratio_
 
plt.plot([i for i in range(X_train.shape[1])],
         [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()

可以看到前40个维度,（注意不是X_train的前40个维度的特征,是降维后,新的坐标系的前40个坐标轴,即第一主成分到第四十主成分）,已经可以表达接近100%的原始信息了.

PCA降维后,我们的数据不像原始数据那样具有可解释性了. 这是PCA的一个缺点. 降维后,在数学的角度上我们可以通过$X=X^{(')}W_k$还原回去得到一个M*N的矩阵,但是这个X与原始的X已经不一样了,因为降维后一定是损失了信息的,所以说只是数学角度上可以还原回去.

PCA降维后,有些时候不但不会降低模型的训练效果,反而提升了训练效果,因为我们损失了一些信息,但是这些不重要的信息可能恰好是影响模型训练的噪音.

---

PCA的一个典型应用,人脸识别中提取特征脸.

from __future__ import print_function
 
from time import time
import logging
import matplotlib.pyplot as plt
 
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.datasets import fetch_lfw_people
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
from sklearn.svm import SVC
 
print(__doc__)
 
# Display progress logs on stdout
logging.basicConfig(level=logging.INFO, format='%(asctime)s %(message)s')
 
# #############################################################################
# Download the data, if not already on disk and load it as numpy arrays
 
lfw_people = fetch_lfw_people(min_faces_per_person=70, resize=0.4)
 
# introspect the images arrays to find the shapes (for plotting)
n_samples, h, w = lfw_people.images.shape
 
# for machine learning we use the 2 data directly (as relative pixel
# positions info is ignored by this model)
X = lfw_people.data
n_features = X.shape[1]
 
# the label to predict is the id of the person
y = lfw_people.target
target_names = lfw_people.target_names
n_classes = target_names.shape[0]
 
print("Total dataset size:")
print("n_samples: %d" % n_samples)
print("n_features: %d" % n_features)
print("n_classes: %d" % n_classes)
 
# #############################################################################
# Split into a training set and a test set using a stratified k fold
 
# split into a training and testing set
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, random_state=42)
 
# #############################################################################
# Compute a PCA (eigenfaces) on the face dataset (treated as unlabeled
# dataset): unsupervised feature extraction / dimensionality reduction
n_components = 150
 
print("Extracting the top %d eigenfaces from %d faces"
      % (n_components, X_train.shape[0]))
t0 = time()
pca = PCA(n_components=n_components, svd_solver='randomized',
          whiten=True).fit(X_train)
print("done in %0.3fs" % (time() - t0))
 
eigenfaces = pca.components_.reshape((n_components, h, w))
 
print("Projecting the input data on the eigenfaces orthonormal basis")
t0 = time()
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("done in %0.3fs" % (time() - t0))
 
# #############################################################################
# Train a SVM classification model
 
print("Fitting the classifier to the training set")
t0 = time()
param_grid = {'C': [1e3, 5e3, 1e4, 5e4, 1e5],
              'gamma': [0.0001, 0.0005, 0.001, 0.005, 0.01, 0.1], }
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'),
                   param_grid, cv=5)
clf = clf.fit(X_train_pca, y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:")
print(clf.best_estimator_)
 
# #############################################################################
# Quantitative evaluation of the model quality on the test set
 
print("Predicting people's names on the test set")
t0 = time()
y_pred = clf.predict(X_test_pca)
print("done in %0.3fs" % (time() - t0))
 
print(classification_report(y_test, y_pred, target_names=target_names))
print(confusion_matrix(y_test, y_pred, labels=range(n_classes)))
 
# #############################################################################
# Qualitative evaluation of the predictions using matplotlib
 
def plot_gallery(images, titles, h, w, n_row=3, n_col=4):
    """Helper function to plot a gallery of portraits"""
    plt.figure(figsize=(1.8 * n_col, 2.4 * n_row))
    plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, hspace=.35)
    for i in range(n_row * n_col):
        plt.subplot(n_row, n_col, i + 1)
        plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray)
        plt.title(titles[i], size=12)
        plt.xticks(())
        plt.yticks(())
 
# plot the result of the prediction on a portion of the test set
 
def title(y_pred, y_test, target_names, i):
    pred_name = target_names[y_pred[i]].rsplit(' ', 1)[-1]
    true_name = target_names[y_test[i]].rsplit(' ', 1)[-1]
    return 'predicted: %s\ntrue:      %s' % (pred_name, true_name)
 
prediction_titles = [title(y_pred, y_test, target_names, i)
                     for i in range(y_pred.shape[0])]
 
plot_gallery(X_test, prediction_titles, h, w)
 
# plot the gallery of the most significative eigenfaces
 
eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]
plot_gallery(eigenfaces, eigenface_titles, h, w)
 
plt.show()

具体详情请参考sklearn官方文档.