洛谷P3396 哈希冲突

分块还真是应用广泛啊......

题意：求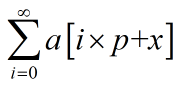

解：以n^0.5为界。

当p小于n^0.5的时候，直接用p²大小的数组储存答案。

预处理n^1.5，修改n^0.5。

当p大于n^0.5的时候，直接按照定义计算，复杂度n^0.5。

所以总复杂度n^1.5，实在是巧妙不堪啊......(什么SB词汇)

 #include <cstdio>
 #include <algorithm>
 #include <cmath>

 const int N = ;

 int fr[N], le[N], re[N];
 int ans[][], a[N];
 char str[];

 int main() {
     int n, m;
     scanf("%d%d", &n, &m);
     int T = sqrt(n);
     for(int i = ; i <= n; i++) {
         scanf("%d", &a[i]);
         fr[i] = (i - ) / T + ;
     }
     for(int i = ; i <= fr[n]; i++) {
         le[i] = re[i - ] + ;
         re[i] = le[i] + T - ;
         if(i == fr[n]) {
             re[i] = n;
         }
     }
     for(int i = ; i <= T; i++) {
         for(int j = ; j <= n; j++) {
             ans[i][j % i] += a[j];
         }
     }

     for(int i = , x, y; i <= m; i++) {
         scanf("%s%d%d", str, &x, &y);
         if(str[] == 'A') { // ask
             if(x <= T) {
                 printf("%d\n", ans[x][y]);
             }
             else {
                 int ans = ;
                 for(int k = ; k * x + y <= n; k++) {
                     ans += a[k * x + y];
                 }
                 printf("%d\n", ans);
             }
         }
         else { // change
             for(int j = ; j <= T; j++) {
                 ans[j][x % j] += y - a[x];
             }
             a[x] = y;
         }
     }

     return ;
 }

AC代码