POJ 3522 Slim Span(极差最小生成树）

　　　　　　　　　　　　　　　　　　　　　　　Slim Span

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 9546		Accepted: 5076

Description

Given an undirected weighted graph G, you should find one of spanning trees specified as follows.

The graph G is an ordered pair (V, E), where V is a set of vertices {v₁, v₂, …, v_n} and E is a set of undirected edges {e₁, e₂, …, e_m}. Each edge e ∈ E has its weight w(e).

A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n − 1 edges. The slimness of a spanning tree T is defined as the difference between the largest weight and the smallest weight among the n − 1 edges of T.

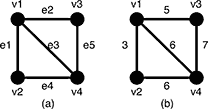
Figure 5: A graph G and the weights of the edges

For example, a graph G in Figure 5(a) has four vertices {v₁, v₂, v₃, v₄} and five undirected edges {e₁, e₂, e₃, e₄, e₅}. The weights of the edges are w(e₁) = 3, w(e₂) = 5, w(e₃) = 6, w(e₄) = 6, w(e₅) = 7 as shown in Figure 5(b).

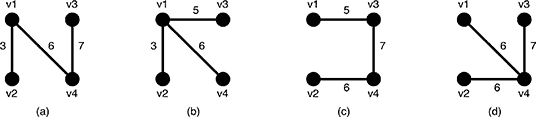
Figure 6: Examples of the spanning trees of G

There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning tree T_a in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the tree T_a is 4. The slimnesses of spanning trees T_b, T_c and T_d shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1.

Your job is to write a program that computes the smallest slimness.

Input

The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.

n	m
a1	b1	w1
	⋮
am	bm	wm

Every input item in a dataset is a non-negative integer. Items in a line are separated by a space. n is the number of the vertices and m the number of the edges. You can assume 2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2. a_kand b_k (k = 1, …, m) are positive integers less than or equal to n, which represent the two vertices v_ak and v_bk connected by the kth edge e_k. w_k is a positive integer less than or equal to 10000, which indicates the weight of e_k. You can assume that the graph G = (V, E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices).

Output

For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, −1 should be printed. An output should not contain extra characters.

Sample Input

4 5
1 2 3
1 3 5
1 4 6
2 4 6
3 4 7
4 6
1 2 10
1 3 100
1 4 90
2 3 20
2 4 80
3 4 40
2 1
1 2 1
3 0
3 1
1 2 1
3 3
1 2 2
2 3 5
1 3 6
5 10
1 2 110
1 3 120
1 4 130
1 5 120
2 3 110
2 4 120
2 5 130
3 4 120
3 5 110
4 5 120
5 10
1 2 9384
1 3 887
1 4 2778
1 5 6916
2 3 7794
2 4 8336
2 5 5387
3 4 493
3 5 6650
4 5 1422
5 8
1 2 1
2 3 100
3 4 100
4 5 100
1 5 50
2 5 50
3 5 50
4 1 150
0 0

Sample Output

1
20
0
-1
-1
1
0
1686
50

思路：
求一个生成树，要求生成树的各边权值极差最小。
一开始想到的Prim，枚举某一个点的每一条边，接下来的扩展尽可能往这条边靠，想了一下，有些许困难。
原因是一个点边的扩展可能有多条，所以不知道我们应该下一步究竟要选那些边。
于是去用kruskal，也是枚举边，就是枚举每一条边，作为起始的第一条边，以此生成最小生成树，比较每一个生成树的极差。
比起prim，kruskal好写一点。。。

代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cstdio>
using namespace std;
int f[10086];
struct node
{
    int x,y;
    int w;
}e[10086];
int n,m;
const int inf = 2100000000;
bool cmp(node a,node b)
{
    return a.w<b.w;
}

int getf(int t)
{
    if(t==f[t]){return t;}
    return f[t]=getf(f[t]);
}

bool Merge(int a,int b)
{
    int s = getf(a);
    int t = getf(b);
    if(s==t){
        return false;
    }
    else{
        f[t]=s;
    }
}

int Kruskal(int s)
{
    int maxx=0;
    int num = 1;
    for(int i=s;i<=m;i++){
        if(Merge(e[i].x,e[i].y)){
            maxx=e[i].w;num++;
        }
    }
    if(num==n)return maxx-e[s].w;
    else return -1;
}

void init()
{
    for(int i=1;i<=n;i++){
        f[i]=i;
    }
}

int main()
{
    while(scanf("%d%d",&n,&m)!=EOF&&n+m){
        for(int i=1;i<=m;i++){
            scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].w);
        }
        sort(e+1,e+m+1,cmp);
        int ans=inf;
        for(int i=1;i<=m;i++){
            init();
            int ansi=Kruskal(i);
            if(ansi==-1){break;}
            ans=min(ans,ansi);
        }
        if(ans==inf){printf("-1\n");}
        else printf("%d\n",ans);
    }
}