二叉排序树(BST)创建,删除,查找操作

binary search tree，中文翻译为二叉搜索树、二叉查找树或者二叉排序树。简称为BST

一：二叉搜索树的定义

他的定义与树的定义是类似的，也是一个递归的定义：

1、要么是一棵空树

2、如果不为空，那么其左子树节点的值都小于根节点的值；右子树节点的值都大于根节点的值

3、其左右子树也是二叉搜索树

在算法导论中的定义：

下图中是BST的两个例子：

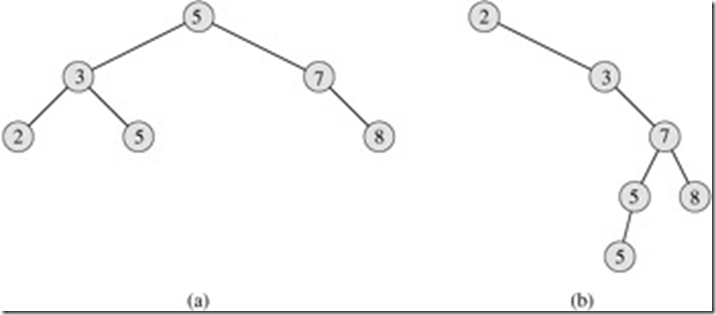
其中(b)图中的树是很不平衡的（所谓不平衡是值左右子树的高度差比较大）

BST在数据结构中占有很重要的地位，一些高级树结构都是其的变种，例如AVL树、红黑树等，因此理解BST对于后续树结构的学习有很好的作用。同时利用BST可以进行排序，称为二叉排序，也是很重要的一种思想。

相关代码如下:

/** 二叉排序树(BST)创建,删除,查找操作 **/
#include<stdio.h>
#include<stdlib.h>
#define LENGTH 15

typedef int ElemType; //数据类型 

typedef struct BiTNode{
    ElemType  data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
}BiTNode,*BiTree; 

/**
 * 向下遍历查找给定结点的相邻节点,以便插入指定节点
 */
void searchBiTreeNode(BiTree &root,BiTree &node){
    if(root == NULL){
        return;
    }
    if(root->data > node->data){
        searchBiTreeNode(root->lchild,node); //递归遍历搜索
        if(root->lchild == NULL){
           root->lchild = node;
        }
    }else if(root->data < node->data){
        searchBiTreeNode(root->rchild,node);
        if(root->rchild == NULL){
           root->rchild = node;
        }
    }
}

/**
 * 插入指定节点node
 */
void insertNode(BiTree &biTree,BiTree &node){
    if(biTree==NULL){
        biTree = node;
    }else{
        searchBiTreeNode(biTree,node);
    }
}

/**
 * 删除指定元素x
 */
void deleteNode(BiTree &root,ElemType x){
    if(root == NULL){
        return;
    }
    if(root->data>x){
        deleteNode(root->lchild,x);
    }else if(root->data<x){
        deleteNode(root->rchild,x);
    }else{ //查找到了删除节点
        if(root->lchild == NULL){ //左子树为空
           BiTree tempNode = root;
           root = root->rchild;
           free(tempNode);
        }else if(root->rchild == NULL){ //右子树为空
           BiTree tempNode = root;
           root = root->lchild;
           free(tempNode);
        }else{  //左右子树都不为空
            //一般的删除策略是左子树的最大数据 或 右子树的最小数据 代替该节点(这里采用查找左子树最大数据来代替)
            BiTree tempNode = root->lchild;
            if(tempNode->rchild!=NULL){
                tempNode = tempNode->rchild;
            }
            root->data = tempNode->data;
            deleteNode(root->lchild,tempNode->data);
        }
    }
}

/**
 * 查找指定元素x所在的节点
 */
BiTree BST_Search(BiTree &root,ElemType x){
    if(root == NULL){
        return NULL;
    }else if(root->data>x){
        return BST_Search(root->lchild,x);
    }else if(root->data<x){
        return BST_Search(root->rchild,x);
    }else{
        return root;
    }
}

/**
 * 二叉排序树创建
 */
void createBiOrderTree(BiTree &biTree,ElemType arr[]){
    for(int i=;i<LENGTH;i++){
        BiTree s = (BiTree)malloc(sizeof(BiTNode));
        s->data = arr[i];
        s->lchild = NULL;
        s->rchild = NULL;
        insertNode(biTree,s);
    }
}

/**
 * 中序打印二叉树
 */
void midSearchBiTreePrint(BiTree &biTree){
    if(biTree == NULL){
        return;
    }
    midSearchBiTreePrint(biTree->lchild);
    printf("%d ",biTree->data);
    midSearchBiTreePrint(biTree->rchild);
}

/**
 * 测试程序入口
 */
int main(){
    ElemType arr[LENGTH] = {,,,,,,,,,,,,,,};
    BiTree biTree = NULL;

    /** 创建二叉排序树,并测试数据 **/
    createBiOrderTree(biTree,arr);
    midSearchBiTreePrint(biTree);
    printf("\n");

    /** 从二叉排序树中删除指定元素,并测试数据 **/
    deleteNode(biTree,);
    midSearchBiTreePrint(biTree);
    printf("\n");

    /** 二叉排序树查找指定元素操作,并测试数据 **/
    BiTree searchNode = BST_Search(biTree,);
    if(searchNode == NULL){
        fprintf(stdout,"没有查找到节点\n");
    }else{
        if(searchNode->lchild==NULL && searchNode->rchild==NULL){ //叶子节点
            printf("所查找的节点x=%d是叶子节点\n",searchNode->data);
        }else{
            if(searchNode->lchild != NULL){
                printf("x=%d所在节点的左孩子: %d\n",searchNode->data,searchNode->lchild->data);
            }
            if(searchNode->rchild != NULL){
                printf("x=%d所在节点的右孩子: %d\n",searchNode->data,searchNode->rchild->data);
            }
        }
    }
    return ;
}

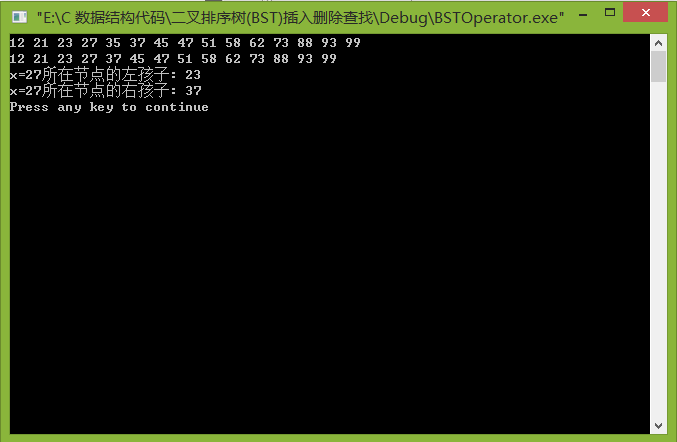
运行结果截图: