最短路径之Dijkstra算法

　　Dijkstra（迪杰斯特拉）算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低。

　　一、算法思想

　　令G = （V，E）为一个带权有向网，把图中的顶点集合V分成两组：已求出最短路径的顶点集合S（初始时S中只有源节点，以后每求得一条最短路径，就将它对应的顶点加入到集合S中，直到全部顶点都加入到S中）；未确定最短路径的顶点集合U-(V-S)。在加入过程中，总保持从源节点v到S中各顶点的最短路径长度不大于从源节点v到V-S中任何顶点的最短路径长度。

　　二、算法描述

　　（1）S为已经找到的从v出发的最短路径的终点集合，它的初始状态为空集

　　

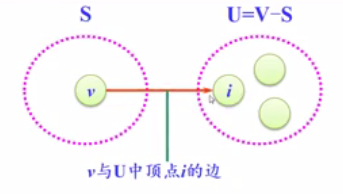
　　（2）从U中选取一个距离v最小的定点u，把u加入S中，（该选定的距离就是v->u的最短路径长度）

　　

　　（3）以u为新考虑的中间点，修改U中各顶点j的最短路径长度：若从源点v到顶点j（j∈U）的最短路径长度（经过顶点u）比原来最短路径长度（不经过顶点u）短，则修改顶点j的最短路径长度

　　

　　

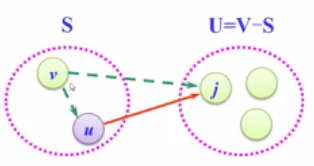
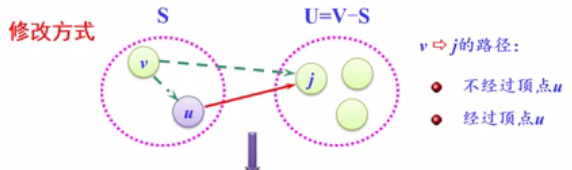
　　　　顶点v到j的最短路径=MIN（Cvk+Wkj，Cvj）

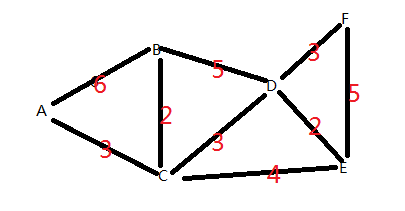
具体执行步骤如下图所示：

S	U	DIST[] {A,  B,  C,  D,  E,  F  }	PATH[] {A,  B,  C,  D,  E,  F  }
｛A｝	{B,  C,  D,  E,  F}	{0,  6,  3,  ∞,  ∞,  ∞}	{A,  A,  A,  -1,  -1,  -1}
{A, B, C}	{D,  E,  F  }	{0,  6,  3,  6,  7,   ∞}	{A,  A,  A,  C,  C,  -1}
{A,B,C,D,E}	{F}	{0,  6,  3,  6,  7,  9}	{A,  A,  A,  C,  C,  D}
{A,B,C,D,E,F}	{0}	{0,  6,  3,  6,  7,  9}	{A,  A,  A,  C,  C,  D}