python拓扑排序

发现自己并没有真的理解拓扑排序，再次学习了下

拓扑排序要满足如下两个条件

• 每个顶点出现且只出现一次。
• 若A在序列中排在B的前面，则在图中不存在从B到A的路径。

拓扑排序算法

任何无回路的顶点活动网（AOV网）N都可以做出拓扑序列：

• 从N中选出一个入度为0的顶点作为序列的下一顶点。
• 从N网中删除所选顶点及其所有的出边。
• 反复执行上面两个步骤，知道已经选出了图中的所有顶点，或者再也找不到入度为非0的顶点时算法结束。

如果剩下入度非0的顶点，就说明N中有回路，不存在拓扑排序。

存在回路，意味着某些活动的开始要以其自己的完成作为先决条件，这种现象成为活动之间的死锁。一种常见的顶点活动网实例是大学课程的先修课程。课程知识有前后练习，一门课可能以其他课程的知识为基础，学生想选修这门课程时，要看是否已修过所有先修课程。如果存在一个回路的话，那就意味着进入了一个循环，那么该同学就毕不了业了。

因此可以说拓扑排序算法是为了做出满足制约关系的工作安排。

下面我们操作一个实例，如下图是一个有向无环图：

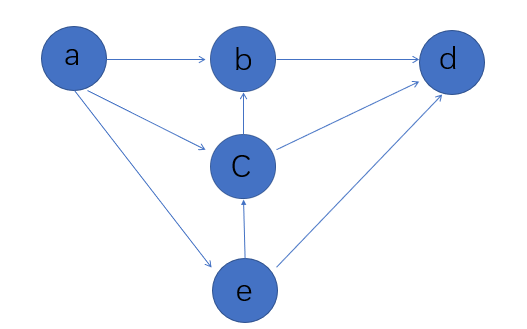
用字典表示：G = { 'a':'bce', 'b':'d','c':'d','d':'','e':'cd'}

代码实现：

def toposort(graph):
    in_degrees = dict((u,0) for u in graph)   #初始化所有顶点入度为0
    vertex_num = len(in_degrees)
    for u in graph:
        for v in graph[u]:
            in_degrees[v] += 1       #计算每个顶点的入度
    Q = [u for u in in_degrees if in_degrees[u] == 0]   # 筛选入度为0的顶点
    Seq = []
    while Q:
        u = Q.pop()       #默认从最后一个删除
        Seq.append(u)
        for v in graph[u]:
            in_degrees[v] -= 1       #移除其所有指向
            if in_degrees[v] == 0:
                Q.append(v)          #再次筛选入度为0的顶点
    if len(Seq) == vertex_num:       #如果循环结束后存在非0入度的顶点说明图中有环，不存在拓扑排序
        return Seq
    else:
        print("there's a circle.")
G = {
    'a':'bce',
    'b':'d',
    'c':'d',
    'd':'',
    'e':'cd'
}
print(toposort(G))

输出结果：

['a', 'e', 'c', 'b', 'd']

图中有环的情况：

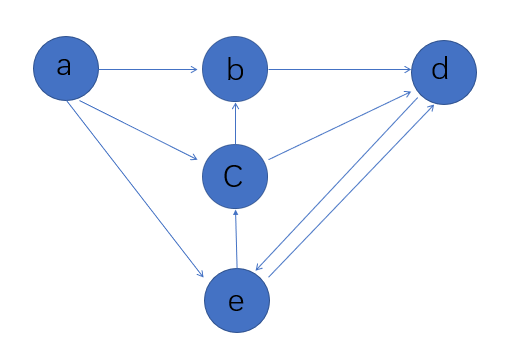
G = { 'a':'bce', 'b':'d','c':'d','d':'e','e':'cd'}

输出结果：

there's a circle.
None

版权声明

作者：赵洁钰Amy

　　出处：http://www.cnblogs.com/zhaojieyu/

　　您的支持是对博主深入思考总结的最大鼓励。

　　本文版权归作者所有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，尊重作者的劳动成果。

　　参考：Inside_Zhang博客

Python 数据结构与算法——拓扑排序:http://blog.csdn.net/lanchunhui/article/details/50957608