HDU 5245 Joyful（期望）

http://acm.hdu.edu.cn/showproblem.php?pid=5245

题意：

给出一个n*m的矩阵格子，现在有k次操作，每次操作随机选择两个格子作为矩形的对角，然后将这范围内的格子填色，现在要求经过k次操作后填色格子的期望值。

思路：

给个格子都是独立的，所以只需要计算出每个格子经过k次操作后被填色的概率即可，最后所有格子相加就是期望值。但是直接求填色概率不好求，求不被填色概率会比较容易。假设一次操作的不被填色概率为p，那么k次之后的概率为p^k，最后该格子填色概率就是1-p^k。

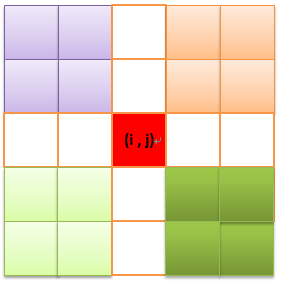
如图所示，假设我们现在要求（i，j）这个格子的不被填色概率，那么我们可以选择的两个格子可以是上部，左部，右部和下部，但是这样的话对角的四个矩形区域重复计算了一次，所以需要减去。

 #include<iostream>
 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 typedef long long ll;
 int m,n,k;

 int main()
 {
     //freopen("in.txt","r",stdin);
     int T;
     scanf("%d",&T);
     int cas = ;
     while(T--)
     {
         scanf("%d%d%d",&n,&m,&k);
         double ans = ;
         double sum = (ll)m*n*m*n;
         for(ll i=;i<=n;i++)
         {
             for(ll j=;j<=m;j++)
             {
                 ll num = ;
                 num += (i-)*m*(i-)*m;  //上
                 num += (n-i)*m*(n-i)*m;  //下
                 num += (j-)*n*(j-)*n;  //左
                 num += (m-j)*n*(m-j)*n;  //右
                 num -= (i-)*(j-)*(i-)*(j-);
                 num -= (i-)*(m-j)*(i-)*(m-j);
                 num -= (n-i)*(j-)*(n-i)*(j-);
                 num -= (n-i)*(m-j)*(n-i)*(m-j);
                 ans +=  - pow(num/sum, k);
             }
         }
         int a = round(ans);
         printf("Case #%d: %d\n",cas++, a);
     }
     return ;
 }