[OpenCV-Python] OpenCV 中的图像处理 部分 IV (三)
部分 IV
OpenCV 中的图像处理
19 Canny 边缘检测
目标
• 了解 Canny 边缘检测的概念
• 学习函数 cv2.Canny()
19.1 原理
Canny 边缘检测是一种非常流行的边缘检测算法,是 John F.Canny 在1986 年提出的。它是一个有很多步构成的算法,我们接下来会逐步介绍。
19.1.1 噪声去除
由于边缘检测很容易受到噪声影响,所以第一步是使用 5x5 的高斯滤波器去除噪声,这个前面我们已经学过了。
19.1.2 计算图像梯度
对平滑后的图像使用 Sobel 算子计算水平方向和竖直方向的一阶导数(图像梯度)(Gx 和 Gy)。根据得到的这两幅梯度图(Gx 和 Gy)找到边界的梯度和方向,公式如下:

梯度的方向一般总是与边界垂直。梯度方向被归为四类:垂直,水平,和两个对角线。
19.1.3 非极大值抑制
在获得梯度的方向和大小之后,应该对整幅图像做一个扫描,去除那些非边界上的点。对每一个像素进行检查,看这个点的梯度是不是周围具有相同梯度方向的点中最大的。如下图所示:

现在你得到的是一个包含“窄边界”的二值图像。
19.1.4 滞后阈值
现在要确定那些边界才是真正的边界。这时我们需要设置两个阈值:minVal 和 maxVal。当图像的灰度梯度高于 maxVal 时被认为是真的边界,那些低于 minVal 的边界会被抛弃。如果介于两者之间的话,就要看这个点是否与某个被确定为真正的边界点相连,如果是就认为它也是边界点,如果不是就抛弃。如下图:

A 高于阈值 maxVal 所以是真正的边界点,C 虽然低于 maxVal 但高于minVal 并且与 A 相连,所以也被认为是真正的边界点。而 B 就会被抛弃,因为他不仅低于 maxVal 而且不与真正的边界点相连。所以选择合适的 maxVal和 minVal 对于能否得到好的结果非常重要。
在这一步一些小的噪声点也会被除去,因为我们假设边界都是一些长的线段。
19.2 OpenCV 中的 Canny 边界检测
在 OpenCV 中只需要一个函数:cv2.Canny(),就可以完成以上几步。
让我们看如何使用这个函数。这个函数的第一个参数是输入图像。第二和第三个分别是 minVal 和 maxVal。第三个参数设置用来计算图像梯度的 Sobel卷积核的大小,默认值为 3。最后一个参数是 L2gradient,它可以用来设定求梯度大小的方程。如果设为 True,就会使用我们上面提到过的方程,否则使用方程: . 代替,默认值为 False。
. 代替,默认值为 False。
import cv2
import numpy as np
from matplotlib import pyplot as plt img = cv2.imread('messi5.jpg',0)
edges = cv2.Canny(img,100,200) plt.subplot(121),plt.imshow(img,cmap = 'gray')
plt.title('Original Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(edges,cmap = 'gray')
plt.title('Edge Image'), plt.xticks([]), plt.yticks([]) plt.show()
结果:
我的结果
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAWQAAACACAYAAAA8uRMAAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4wLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvpW3flQAAIABJREFUeJzsvXmUXHd1Lvr9ap6nniepNcvCMni2EoxtDHn3YjwAAZKX5wDJdR5JuBdYuYF7CYMJPBwM5AYeBmfdtwIhTuKEgAGTmBAHDzKWLUe2PMiyLbXUrVYP1TVXnZqH8/6o/nb/qqyhS25ZLan2Wr26u06d+Zzvt3/f/vbeyjRNdK1rXeta1868Wc70AXSta13rWtea1gXkrnWta11bJdYF5K51rWtdWyXWBeSuda1rXVsl1gXkrnWta11bJdYF5K51rWtdWyV2XgCyUupTSqn/b6W/u4xtmUqpjSuxra51rRNTSo0vPn+2M30sXVu+nXWArJT6oFLqeaVUQSk1r5T6tlIqdKJ1TNP8kmma/2U52+/ku6/FlFIPK6VO+366du6YUmpSKVVUShnazzfP0HG87fXe7/lgZxUgK6X+CMCXAfwxgCCAqwCsBfBvSinHcdbpeghdO5fsRtM0fdrPR870AXVt5eysAWSlVADA5wH8V9M0f2aaZtU0zUkA70MTlP+vxe/drpT6J6XUPUqpLIAPLn52j7at31ZKTSmlEkqpz+gjvv5dbdr3AaXUEaVUXCn1J9p2rlBK7VJKpZVSc0qpbx5vYDjJuV2rlDqqlPqEUmphcVu3KKXeoZR6RSmVVEp9arn7VUr9mlLqZaVURin1LaXUI7o3rpT6HaXUfqVUSin1r0qptZ0ec9dWlymlrEqpry4+o4cA3NC2fJ1S6lGlVE4p9aBS6q62d+IqpdTji8/Us0qpa5e53w8qpX6plPpfi+seUkr9yuLn04vP8we079+glHpGKZVdXH572/ZO9G5alFL/Qyk1sbj8H5VSkddw2VadnTWADOBXALgA/FD/0DRNA8ADAN6ufXwzgH8CEALwt/r3lVLbAHwLwG8BGELT0x45yb7fDGALgOsBfFYpdcHi53UAHwfQC2DH4vI/6PC8aINont8IgM8C+N9oDjKXArh6cb/rT7ZfpVQvmuf+PwH0AHgZzWuHxeW3APgUgHcD6AOwE8Dfn+Ixd2312G0A3gngYgCXAfj1tuV/B2A3ms/E7QBu5QKl1AiAfwbwRQARAP8dwA+UUn3L3PeVAJ5b3PbfAbgXwOUANqL5DH9TKeVb/G4ewG+j+W7eAOD3F5/J5byb/w3ALQCuATAMIAXgrmUe49lhpmmeFT9o3tj54yz7MwD/tvj37QAebVt+O4B7Fv/+LIC/15Z5AFQAvO0Y3x0HYAIY1b6/G8BvHOc4PgbgPu1/E8DG43z3YQD/ZfHvawEUAVgX//cvrnul9v09AG452X7RfNh3acsUgGltXw8A+F1tuQVAAcDaM32Puz8nfQcmARgA0trPbYvLfgHgw9p3f23xGbIBWAOgBsCjLb9He84/CeBv2vb1rwA+cILj4PvyQQAHtGXbF/c7oH2WAPCm42zrLwD8r8W/T/Zu7gdwvbZ8CEAVgO1M35uV+jmb+NU4gF6llM00zVrbsqHF5bTpE2xnWF9ummZBKZU4yb7ntb8LAHwAoJTaDODP0fRIPGg+/HtOsq3jWcI0zfri38XF31FteXGZ+20/P1MpdVTbzloAX1dKfU37TKHpiUyd4rF37fWzW0zTfPAYn7fcd7Tey2EASdM0C9pn0wDGFv9eC+C9SqkbteV2AA8t85jan1OYpnm8Z/dKNB2oCwE4ADgBfP9Y53CMd3MtgPuUUg3tszqAAQAzyzzWVW1nE2WxC0AZzam2mFLKC+A/A/h37eMTlbCbAzCqre9Gc6p1KvZtAC8B2GSaZgBNKkCd4rZWar/t56f0/9F84P9v0zRD2o/bNM3HX4fj7trpszksASzQ9Ir1ZRGllEf7TP/uNJoesv5MeE3T/LPTcJx/B+AnAMZM0wwCuBvHf3bb381pAP+57ThdpmmeE2AMnEWAbJpmBs2g3v+rlPpPSim7UmoczdH1KIC/Weam/gnAjYuBB8fiNk8VRP0AsgAMpdRWAL9/ittZyf3+M4Dti0FBG4A/RJOfpt0N4H8qpd4AAEqpoFLqva/TcXft9Nk/AvhvSqlRpVQYwP/gAtM0pwD8B4DblVIOpdQOALo3fA+a78T/sRgcdC0Gmkex8uZH01svKaWuAPB/astO9m7eDeD/YRBaKdWnlLr5NBzjGbOzBpABwDTNO9H0Br+KJiA9ieaoeb1pmuVlbmMfgP+KZuBhDkAOwAKa3nen9t/RfKByaAbh/uEUtnEqdtz9mqYZB/BeAHeiyd1tQ/NlLC8uvw9N6eC9qqlCeQHNGUbXzg67X7XqkO9b/Px/o8n7PgvgabQFv9EMlO1A85n4IprPDJ+JaTQD4Z8CEEPznfpjnB58+AMAf6qUyqHJGf8jFyzj3fw6mt71zxfXfwLNgOI5Y2qRHD9vbTH6m0Zz+n/4TB/PSptSyoLmDOK3TNNcLifYtXPclFL/AOAl0zQ/d6aP5Xh2rr+bx7KzykNeKVNK3aiU8izyz18F8DyakeNzwhanniGllBNL/PITZ/iwunYGTSl1uVJqw6KW9z+h6RH/6EwfV7ud6+/myey8BGQ0H8bZxZ9NaMrYzqWpwg4AE2gqT25EMzJfPPEqXTvHbRBNqaUB4BsAft80zWfO6BEd2871d/OEdt5TFl3rWte6tlrsfPWQu9a1rnVt1VlHiSE2m810uVwwTRO1Wg31eh2maUIp1fKjm8VigdVqhVIK9XodjUYD9XodFosFFosFHo8HTqcTdrsdFouFGTiy3eVY+/e4bqPRQK1WQ7lchmEYssw0TTQaDfn/RNu1WCxyXvqx6efXvm/9t1JKzt9qtcI0TTl/q9Uq61erVdRqNbkuAGC321uuS71eR6FQkG1brVbYbDZYLBa5rtVqVe6Lfm/aj8dqtcox1+t1WcZro2VDyXna7XbZJ7+r70u/ttyHzWaT+9D+Xf2ZsVgsKJfLqFarr4eOu8WUUt1pYtdOq5mmuaznuiNAdrvduPrqq5HL5XDw4EFkMhkATWBwOBzyovJldTgc6OnpgdfrBQAkEgkYhoF8Pg+3242+vj5cfPHFGB8fRyQSgcPhQC6XQ7VaFSAEmmBAsCKomaYJi8UiL3yj0WgBMwAolUpIp9OIRqN45plnUKvVUK1WUa1W+fLLZ/pgYrM1L4vD4YDX65Vz4zo6AAIQwFFKoVwuy7acTidcLhd6enrg8/ng8zXT+QuFAjKZjABXvV5HPB6HxWJBb28vvF4vbDYbXC4XAoEAAoEAqtUqcrkcJicnkc/nUavVYLVaEQwG5fgMw0A6nUalUkGlUoHVaoXb7YbVakWpVEI2m0W5XIbL5YLT6YTVapXzCIVCcLvdsNlsqFaryGQyKJVKcr5OpxMDAwPo7+/H4OAgfD4fSqUSkskkstksKpWKrJfP5+F0OtHX1we/349Go4FyuYx6vY5KpSLPgM1mg9frhVIKfr8fe/acapJj17p2blhHgExPxm63w+PxIJvNipdUKpVgt9tbvuv1ehEOhxEIBGAYBmq1GgzDQLVahc1mE88RACqVCvL5vACKx+OBy+USr1r38LhuvV4XEHQ4HGg0GqhWq2g0GnC5XCiVSigWi80ccZut5dgIoLRGowGn0wm/3y/AWa1WxeOjp12pVOByudBoNF61Pj/jcXE9oDlo0eOtVCqo1+vIZDIoFAqwWCyo1+twu91oNBrweDxwOByoVqvI5/NoNBoolUpyzFy/VqshGo3C5XLJ+VksFjgcDvj9fjidTgH3YrEIn8+H+fl5uU7cjs/ng9/vh9/vl+34fD7kcjnxyF0ul9wvgi89fNM0Wwa3bDYr96lWq8Hj8cBut8PtdkMpJb85aDgcDng8nhavvWtdOx+tI0Dmi2yaJvx+P2KxGCqViniMuqfp9XoFoAlMtVpNvFsCLdCc3huGgVKphEqlgkajAYfDIdP1crks3i+9SofDIWALAOVyUzterVZRKBTQaDQEcHTPl1Np7pPbJFBEIhF4PB4opVCtVlEsFpHP5+V46VHSIweWKBOCMI2fl0ol8ZZ5PbgNDiQc7HTKoF6vo16viyfLcyKAl0ol2Q/Pn+eplILdbkcgEIDNZhNqI5/Py3Wjl83r4na7Ybfb5V45HA5UKpWWgYCzG85Q8vm8zDhyuRwMw0Aul4PFYkEul4NpmrBarXA6nXA4HCDl5fP5kEql5Drr161rXTtfrSNArtVqyGazAmjBYBDJZFJAkWDp9XoRDAbh9/tlGpvNZoXfJKAYhoFsNotEolk/hLyi1+sVz47/0yMDIODscDhkv4ZhwO12o1arCWg5HA4BBK5Xr9dhs9lkKs/vKqXg8/kQCAQQCjUbkJRKJTQaDeTzedjtdpRKJQFdfWDhcRPceUw85nK5LNdNH2ACgYB40LVaDU6nE263W7bp8XharrtpmrDb7XC5XHC5XFBKyYABLM0eeC05i6Bx5kDjgMXrzMEQgFA7tVpNBgLSDdFoFE6nEz09PeL5AxBQ5mCTSqXk+obDYRmkOQA4nU6hLnK5XBeUu3beW0eATBB1uVzikZHfBZqA4HA44Ha74fF4hN8lt1kul1uCdZVKBYlEQjwncsQulwvFYlG2oQfXrFar7I/75oCQSCTEWyOwtQeqbDabACkBzOfzCSCT+9XpCqfTKeBM75aeq266x89jJrVQqVSEX9Y5ct1rJ9VAj1i/7sViETabDX6/H6FQCJVKRfjeQqFZxIvX0eFwCL1QLBblOAmCAOQYgObAQ0rJ4XCgVquhUCgITVKr1VAsFluOh8HYYDDYfJBsNtjt9haOnRQGz50cMr/DGEC1Wu3kMexa185Z6xiQo9EoIpGI0AlWq7WFqnC5XAiFQujv74dSSoJDpCT0oJ9hGJienkaxWEQkEoHVaoXH4xHA41SfQUFyqXqkn2BRKpWwsLCAQqEgdAfBR1c1ECB1BQGn9wRGgod+3rpCgP/T+9OVGDw3faAimCcSCQFbevB9fX1wOBxwOBxwOp0yWLlcLgFFbouATNC02WwoFArI5XKw2WwIBoPw+Xxy/rxm+kDhdDpFjaFbpVIBAAmq5vP5lpnPsVQvTqcToVBIgLVYLArI8/5wwLDZbC33lqBMKqVdrdK1rp2P1nFQT+eI6QHp3rIu2dKDProyggDGqbBhGAgEAnA4HBLZLxQK8Hg88Hg8KBaLcDqdElgj0NHbzefzWFhYwNzcHAqFAgYHB+F0OgWQAbwK6Onx0UMlSLtcLni9XuFOa7Vai3fMQYDXg140z4m8LD1kXo9isfgqPtvj8cDtdgt3Gw6HUS6X5XryGDiI8Lr6fD45FwKv3W6H3+8XOsPlcqFSqbR4vPyM58RBwePxSCCTAyepCp2iaffqK5VKy+ekU/T7zc8sFotID/VZAxUiXUDuWtdOAZADgYBIswhk5DcJUJyi8qUlp6hP8fki8+WkZ0uVAj05esC5XA52ux2FQkGAiHxppVIRWRe9QLvd3uLRERwJdgQEAOJRUtpWKpVgmmbLlB2AAAdBWPeGOU3Xf3P/9K65b10LzGAaAb/RaIgkLpPJyHXUtb38X98O/+Z5cLbC/7ltm80m1AbPKRAICP/OQZIDiE77kJdmDIH3TVeO6FpyKis4QNhsNuGiC4WCzDDIh3eta+e7dQzIDLjpPCa5Q6A5PeeLTCACmqBHDhWATFe5LoM7fIEJVPSa8/k8DMOAaZpwu92iHgAAr9eL/v5+AeGenh6RUZEL1l94erw8PsqvKDGjt5xMJpHL5VoSNnQNsu7x8vro3G978omuxuCgwUAeg4cMguZyOQmyMThIPpbqD31QaTQaIqHjYMKgZrv+mka+3u12IxgMwmq1Ch+dSqUkaMrZhO5R0/Om0oMDJ68hPWlKHznrMAwDhmEIKFNh0QXkrnWtQ0C2Wq2IRCKwWCziEbUHtgiyuveXz+fhcrkEtBnACgaDLZI46om5HXKqBK5isQi73Y5QKIRAIACfzydARe+Q6gSdrqAXSy+xXVpGr3xmZgaRSASRSASlUgnxeFxAm9IxepnAUoYbt8Nz0zlXeo36ceg0BT1SJk+k02lks1lJuuG1aA8otvO7ulaZnrxObxQKBfGAgSWQ1QdMXWYYDodlkLTZbEJxeDweBINBoUoouWPSDK8Bqa1qtQqXywW/3y9grB9vo9GQAGxXZdG18906AuT2zDtmspmmidnZWZimiUgkgsHBQVELEHTS6bRwiB6PB319fejt7RWpVDwel6lyX18fgsGgeHfkIkOhEOx2OwYHBxEMBkUvXCqVBDhqtZoAOL11AAIW9DAJTqQCyEWXy2XE4/GWJA8CvQ6sOqi3pzDrOmN6zaQx+F2dzwYg2XSNRgNerxeBQADlclmAlPvTA2L6AFOv10X/S90wKSAm2FCD3G4ulwuRSES8dq/Xi97eXlgsFlSrVeGBqXyhx0uvmLpvAOIV04smmOdyOaGDMpmMKDU463A6nauOR+4kfb9rXVsJ6wiQyUdWKhWEQiH4/X709vZiZGQEExMTOHDgAHw+H9xuN3p7eyVAR0UCvSa/349IJIKenh7hi9PpNHK5HPL5POLxOObm5rBmzRq4XC7J9NIlYQSmRqOBYrEIwzBQLBYlmMYkBnLOut6XHqkOmMBSkI7cJzW1BG/dM+X3dQ+eswVSC7pH6nQ6JQjZnuHHQYISO10j7XQ6RcfNhAxgaZZBbrZWq0kCC89B57u9Xq/IFpmwwQQfzlQASCpzOp2Gy+VqkRgyezIQCMDv98t1JB9cr9fh9Xpl0A4Gg6jX6+L5V6tVJJNJGIYhOnXOlHSve7UYn4cuKHft9bKOOWRSARaLBT09PSJtGxgYwNzcHICmZ0HJFrlfph1T4kUukpI5ghk50Wg0inw+j4GBAQwODiIQCACApF8zy40a3Ww2K9N1pZQANHlZu90uCRn0iPXz4v/BYBDbt2+Hx+NBJpPBk08+KcFLvph61qEu8yIw6h4wAAmu0RtnMgaPg58T/AiK9P7pOfO6kxIiIJO20SV9VJmQH240GrDb7Uin0y2JLRw4qGQhZWS1WgW8qXBhUJXHQm6awb16vS7yvWAwiEAgIM8C7xH1zrwuTJAJBoOrzkMGXl24aqXs9Qb67sBydlhHgMyAk9/vb5E/6SnVDNyUy2UUi0XEYjHkcjlkMhmhAOhR6QoGPTWZ9AJBjZ4sI/TZbFa4XIIQa2kwYs+pcrFYFEDWAUsHJYKf1WrF1q1b0dfXB6BZTGlgYADRaFTkdu2JJrraop2r1lUNDGLqFIbD4UAkEmnhaMlpE2SLxWJLMBRYAgkCe3vKtR4w9Xq9iEQich15fXjcSinRMnMZZzaNRkNmLdye3W4X3TN54HQ6LcoUqkvISZOaIFjrx68rNlYjZXE67fUGxy4Ynx3WESAzmYOecjqdhsViQaFQQKFQQCqVgtPplKk2A2OsncAgD7W1Oh0ANCkRPaKv1zng9LhWqyEWiyGdTovOmQkTlMqRL2XZTV0WRtMTRQhMnJZ7PB4ZGKiA4Hd0GRiDmsxAJC3RrtslWBKYOb03TVN4XgByvkzKIH+sl7skFUNKQ88o5DnqtSt0jlmX4/G7XLdSqSCXy7UMfLzmekKMw+FAOp0W5QkLEJHSodKFqhGdhqAHzvvPIG4ymZRBsGuvj3U95tVpHQOyaZooFotIJBJIJBIoFouYn58XL1J/ielV6oDGF57eF4Giv78fjUYDCwsLSCQS4j3XajWkUinZpmEYmJ+fRyqVgtVqhc/nQ19fnwSgCFrZbFaATdclE2zJjxqGIbpfAKKrBSDnqVMVrGlBcKfXTACnV8jrRfWEDkQcIBhIpPSPATLOGihtI8/O4KKupebfOj9NekTXXuu1P+ix8r4YhiHKEQ6IlN253W4AS9mO+Xwe0WhUdMqZTEbiAwBkENSPl9eGHj1jERycGOjrqixOn7UDcBeMV6d1zCGTl6VXzHrDBCbK0aiIsFgsSKVSom8FILUWOE23Wq3o7e0VD7hSqSAejyOXywkPzfXJaxYKBQFYyruY3FAqlSSiT5AmR8uglNvtFvCgV+p0OmEYBl5++WUBPhbuIQC7XC784R/+IarVKu6//35ce+21+OEPf4hEIiGgyGtFMOIPA3+soqYH1wAgk8m0yNYoJWNaNEtkkgsmaOqFlEjXkIrQOV96/MPDw3Ivef6pVOpVlIzNZkN/f78cL2dEBFKPx4PBwUE0Gg2R6lWrVUmVp66Z4G2apkgUeY4coHV9dNdW3k4GwHpiVxesz5x17CFTc0rwIjDS6/N4PAiFQohEIgCAcDgsgAc0gY1gTcqAhdbpsTKLjFNy/jD1l2oKctgAxKvVAY5Gb5GcKrlQBtuSyaRoeNPptJTETCQS4u0qpfCud70LfX19ePrppzE4OIhbb70VDz/8MH7nd34Hf/7nfy7TenKheuCPHjrpBC6nR05Q1QOG9I6p4tABXwd7Dmp8kfidSqWCVCqFcDjcQimwkh61zul0Gkq1poST++3p6RGdMIGZwUsOgrxGrGrH8+f94gwHWMp25HHyeun1qrt2eq0LuqvXOgZkoFm8nIEoghuTJ1ifgfpkZtARXJhGqwfFCKqsvNbT0yMBOS7jy2u329Hb2yt8Kz1tVo2jSoO1IarVqqgN6H3a7XZEIhEBCQ4eBOVEIoFsNotCoQC/34+BgQG85z3vwfPPP48XX3wRuVwOhw4dQr1eR29vL5599lkMDQ2JxwssFSwClpIuGLhyOp0ycOilQAnMzLjTk13oWft8PlEmMK2aXLCetsyXjoMNAAHY9rKZLP5Dzplp7MFgUACZxoAegJYuI16vF41Go4XC0JNXGAvgOddqNdFN+3y+brbe62jt17n9mWn/vHtfXj/rCJCZZUbvkqm4fLE5JadUiwoDn8+HsbExLCwsiBeYz+clicHr9cp2mM4bCoUkCAYs1fL1eDzw+/3CJxNEs9msdNkgwFGupWe4AUvZZQzQUd88MDAgUq2jR4/CYrFg/fr1WL9+PXbu3In9+/cjFAohnU6jt7dXpH0AcMstt0j9Xz09nDMAgiY930wmA9M0BeyYcswBiJSBHoijpw0sldokhdFeq5m0AIAWJQuvLymcYrEoWmYOaPSCOfNxOp3Cg3Ng0VOjWcuChZlYYIkDMe+DHkTUU9rJabfPbLp2eqydVmsHYT3I3P5ZJ9vuWufWMYfc29sr02eCwtzcHJRS0q6JmXl+v18A1G63i1aYtX057dVrRBB46Dlyv7pelZrkXC6H+fl5UV3wYWAWIIEnlUoJ8LA+hl7SkgMAI/0WiwXbtm3D2NgYDhw4gOeeew7ZbFbaGs3OzmJmZgb79++HzWbD1q1bkc1mEY1G8e53v7tFucHtESSpPmCfPHr5uu5XV2no+mwmnDidTpmJDA8Po1AoIJvNIhaLiUZb3x+wROVwEGWCDzP5aNw2uXh6z3rAlusXi0XJ2uTMJBgMYmhoCJFIBLlcDolEokVxAizJ3QKBAPr6+uByuaSuctdOv+kyzXbgbAfhTumNLhC/Nuu4lkUoFBLagSmy9Pr0ABC9YGZ3maaJtWvXIpPJYG5uDqZpIhAIwOv1CkhyWtte/0GPzvv9fgQCAfHQmHZNxYZpmsJRE3ipvGBSC4uiUyvNYB8AAfH169fjhz/8Iebm5mC1WnHw4EGMjY21qA6ovX322WexceNGvOENbxBel/vRvV4qG3QVBrl11rBIpVKyrr4OsFQ9jTMJ3hN6qtQr85rxN8+VgTyqRCh3Y8KOPnAwOEevv16vI5vNyszHYrHA6/XCMAy5d9VqVbLueN+pZtHlb41GQ1KwmdWnDwpdO/12MuDUveQu5/z6WcceMj1jvWtxIBBAvV6XTiFUEDBIZ7FYhGaoVCryNzs6e71e8YoJHpRiUa9Kj47AomuQmbFH4CIY6V4Zp/4ECiY1EFjJb/Ph27lzJ5599lmUy2WMj4/DYrGICoJcL/ejlEI0GoVSCv39/S1crl4TGVgKjFKPzcQVJtDomX56XQwdoFm4nwX9uR89UUeXHnLApKKBnnKhUGjxfPUKdFS7JJNJUUDkcjnZFxNWOBjk83lkMhnhg0mTAK1p45wJsXYzqQ2dUura6bMuuK5u6ziox2k0gYZ/EzSoULDb7VLMhhwkg1Xkn9/+9rfjueeew7p164T22LhxI3bv3i0cJqfLnCobhiGcL6fVujoAaGppi8UiwuGwcMR6QXZ2pKYelmnVhw8fhtVqxYYNG8RTfdOb3oQnn3wSpmkiHA5L4G7Lli0wDAPJZBLVahWhUAjXXXcdHnroIUSjUQFBnq+eLg1AVBf0YvWBhss50yAgsmrezMyMbJMzlUajIYMYrw3Bl6BMXpoecDKZRD6fF4AHlmYIvEdMQSdY8n7wh8k8hUIB+Xwe2WxWZjCcgfDe6MHbcrks++As4VzRIetc+KnwsKfLlnsMq+FYz1fruOs0QZVTWmbE0Xvl9JUyKraF7+npEU+R3SsuvfRSXHnllQiFQjL9z+VyeNe73oWPfOQjLS8x5W4ul0uK1etaYwas9HRqKjtIV9AzJd+pqwd4zHa7Hf39/Xj44Yfh8/mwd+9e8YQPHz4slMHU1BQuvvhifPnLX8bzzz+Phx9+GB6PBxs3bhT6gXQMeXJgKYGDtAw9UiZIEPyoL6bxWhLgKCUjNcPaIPRO+aNrsfVynLxWnB2QtmHaMxUtXM6MRN3TpVKC94565N27d4v8kZmPuqyNXnIqlUIsFpMEomNVojvb7HhgthoAbrlgfCrrdW1lrCNArlQqmJmZkaktwZJeICVbBBZ6ieVyGVNTU9I8FACy2Sw++clP4ktf+pIkHNx5553YunUrbrjhBnz3u9/F7/3e70liAz1cbpMAsbCwgGw2K8BEoMnn89IRm8ErSsiYUUcvld5fLBaDw+HAvn374Ha7Ua1WhRKw2WwYHR3F9u3bkUql8N73vhfr16/H0aNHceWVV+I73/kO5ufncckll2DNmjWiOqDUjDQAOV0eE7W8Sina7dKgAAAgAElEQVQJGCYSCfH89cFFT4PW61foCRb0MvW/OTgS7CmX44BK9QO3q6/HoB8Bm+npHCyTyaRUkqNMkYMCi+TTCFbk1Zlgks1mW1pznc12PMXCavA6T6SA4PGd6BhXwzmc69YxIFNZQL2wz+eTgAwz6vhbLzRDQNA1qdu2bcOXvvQleDwebNq0CR/72McQDAZhs9lw6NAhfOITn8DAwAB+4zd+A8ASZUKFBr0/vSC6Xn+Z4F8ulxEKhSTIptcU5mACNAeWubk5vPOd78Qvf/lL6XLC4OGOHTvw/e9/H7fffjvy+Tx8Ph/e+MY3YmZmBps3b8bIyAgqlQrWrl0LAAJguvaaMwsG1qhAsVqtIhmjokJXaVBpooMx6RaeNwNzXK7L/IDmLIAqDl4XtuKizlkPSlIzrS/jd+kpE0g5SLYfLwefdg+ZdE57tb9zwXRwWw7QvV52omNYzvGthnM4161jDpkFaJRaapXk8/lgmiYymYzwiGxSSoAEIEBIMIzH4wiHw3C5XJifn8f3vvc9bNy4ERdddJFkgOXzeXzta1+Dx+PBJz/5SQQCAYTDYeFHWexcr7qmFy2iB6wDBoCW7D+9bnImk8HevXths9mQzWbhdDqRy+Xg8/mQTqfxB3/wB+jt7ZVkEtNsFgjavHkzSqUS/H4/arWaBD4Jxu3dnvVKcAx6kRPWZYCkNegN07OnJ6qUkv2wIDywRAtQSWEYBur1urRmstvtIiPUC9pz8NQTNdi9pV1OR6AGmpSKXk7VNE2R0PF49DofesCSsYJzpdqbDlyryUM+nq3mYztVO1vPqWNAJp+oUxZcRi84lUrJC06+tr1xKME6FArB5/NJssQDDzyA73//+xgZGcG6detgs9lwxRVXIBQK4Qtf+IK0mt+7dy/27dsHr9fbUhWNwTO32y0SPWpp+eJT/jU3NydJDnq/ueeffx7JZBI2mw09PT0IBAJYWFiA3W7HSy+9hEceeQSzs7P4zd/8TYyOjqJUKmHNmjV45ZVXRHVAD5YeJR8OPQDJmQJBmly4nnoNoIUiCAaDwkmTiiAw6sFWnXpgcSHqhp1OJ8bHx9HX1ycDFu8Tp7U8Fj0bUH/AdcpED/i1e4f6eejPCakjfYB6+OGHO3kczyo7FjCvlsy49v2dKHHkbLGz8ZiBDgEZaOpe3W43+vv7xfuh19Tb2wuPx4NIJCKesj795YtJUTqwVDdB1wRXKhW88MIL4knfcMMNACDFdUqlEi699FLs2LEDQDMRpFqt4sc//jH+4R/+QdJ+BwcHhebI5/MCBPyM3CVld3pSxtq1a1GpVLB161aUy2VcdtllWLNmDex2u6gcyCv39vbigQcekAGHATSCHIAWqoTHQO+VEjidhtG7mjCoyEGQ6+q1nynF43KdIqDqgiVAqfvlNlmYSNdM65pkbkMP6C2Ha2yXBuq1qDmr4f/AUj2SM2knAqCVAKcTecync7/t22pXguj7OFvB7FywjlOnd+zYgdHRUYTDYQAQ2ZLP50M4HBaelm2Hnn32WaRSKfGI6GXr6bMAhFdlwaJ6vY6XXnoJFosFn/70p7F+/Xq8613vkkywRqOBWCyGQCCAQqEAt9uN97znPbjpppsQDAZx1113IRAISPCM1dEGBgakwA9piU2bNmFhYUFqXhQKBTidTtxyyy145JFHcM011wgNs27dOnziE5+A1WrF7t27EYlEkEwm8bOf/QzDw8PYvn07SqUSnn76afE8BwYG8Ja3vAWHDx8WvS2laHpRJKZz6zI/nXYhpcHUdT3Qpw987VwusNTRRJ8J6DJFAi49bnrYeiBOD/rpWYDtOmtSLTz29iBhe9IB/z6Tthyu93Qc43LAdiX3e6xrf6J9LPd7XVsZ6wiQPR4PLrnkEgwNDQlvzECR3++XbsrMQGMVsRdeeAGzs7PyclKjSo+JYJzNZiXjjsE7l8slKdePPvooLrjgAiwsLGDLli0YHR2VVGSCn9vtRqVSwUc+8hEMDAzgO9/5Dux2Oy677DL09PTgmmuuEeXFwsICPvvZzyKbzQqFwgzDmZkZ7Nu3T2paAMD09DTi8TgmJyeRSCQkZfrIkSMYHByEx+PBwYMHYbPZMDAwIA9vNpvFgw8+KFwygdFisYgemp4yQVjvbqLz4Cx8xGCb1+uV9GVeX/K19LDpnQLNwCulZmvWrIHX6xUFC41eLWWFXEZahKYHU/XKfTpV0T4T0rumcMbA+32mEkMuvfTSUwKa1+K5tgPjqW7nWOuebJA73uCzmiV754t13OS0v78fvb298Pv9MuUOBAKSNUaPj0GmZDKJoaEhzMzMiGesR9iZXEC5nF7wnb9dLheOHDkiUrorrrgCU1NT0t2aOl56hwS9+++/H/v37xdvu1Qq4d57723pA2ez2RAKhSTjEGh66263G5OTk/D5fFi/fj327Nkj5+z1elEsFvHUU09JOUsWy2diBABRetjtdszNzWFsbAy5XA6BQKDFk+ULpHukBDcuJ1VAT5kBSdIVuvytvZBRuyqFyS0zMzMSJNTpJF6DQqGAeDzefFAWlTX8m2Cse9L0rDnAMOGD6+geOwcJtogix3022UoBVaegfDJ6YTket05dtG+r01nLapnlnAvWcS0LBpXIZzKyrr+krKVrms26EgRsXQ7FJBPWH9a7IQOtIEQgisfjMAwDzzzzDC644AJs3boVkUgEPp8P/f39iEQiLaP/jTfeiGeeeQbFYhGDg4NSwMcwDADAunXrACx5cslkEkCTkyYN4vV6sWHDBjz11FOyXiwWw8zMDBKJBILBoHRoJhizWHs+n0cwGMTk5CQajQYOHDiAv/zLv8Rdd93V0mdPpxgoY+NyPWjG68IXiT8MDgJL6e3UMHM2UiqVJPNPb/rKZB5ul/eQgUIOPpTrkarQ+WoAQmOwuBSTStoVI/SkeS7kzvn/+WqdqDFWwps/HqCfLKB3rKBkF4hXzjoO6jHgpIMr6/zqLyi7dpCaYOdkghA50mQyKY0zCewEEv4GICDDfR88eBAvvfQSEokEtm/fjquvvloCcTabDb29vdi1axempqbQ09Mjxx+PxzE6OoqnnnoK4XBYqsIxo7BQKMA0TQwNDaFWq2F2dhZ33nknxsbGUKlUEAqF5Hx+67d+C8FgEFu2bMHevXvh9Xpx4MABqR73i1/8AqFQCKFQCIVCAdVqFXfffbdQMQQrPvz0Vrmc2XtKKUky4fVho1hdSqcDHUGa9Ai5Yc5SKpWKzBAI5uwfSIqCxYyoCCGA6lmGuhLENE2hrICljEwGE3UvnsfKbenxhPPZ2lUXK+mFt2/3WOB7Il7/RPfnbFVjrDbrCJBrtRoWFhZQrVbh8/lEDsUXl3WIKX2LxWI4cuQIJiYmhIpgcXYa9bF8Qal31SkL/hA8Go2GdA3x+XyYmZnBj3/8Y9TrdQwMDMDtduPaa6/F9773PXz84x/H5z//eVx++eUAlkp5vvGNb4TX60U0GsWePXukzvH4+DhKpRJCoRAmJyexfv167Nq1Cx//+Mdhmib+4i/+AoODg3jDG96ARCKBiYkJHD58GOFwGGNjY7jhhhtQr9fxs5/9DO9///uRSqUQCoWEt56ensbdd9+N+++/HzMzMy16Yb1YksfjkWUcYFjetF6vI5FIIJVKIZ1Oy/WgUQtMjprqCCo3yLdTy02vuVQqSS0LXSZI7lv/Hj1ivoQ8h1gsBmBJc87z0nXgfOl1DpnbOJvsdIPQ8SRxJ1OCHGv99uXL5Z7bQfhYXnbXVs5UJ16J3+833/3ud4tsyuFwCBD7/X709fVJkO3AgQOYmJjAk08+iXw+L99j4gEAqc2gVxtjF2ZyqEx2YGEgPS2XXDSTK/hi89jYhDUajaKnpwcOhwNXXXWVUA8srs4Skky17unpwc033wyLxYLPfOYzKBaLSCaTuPHGG/HII48gmUzCarWip6cHfr8fIyMj+Pu//3uYpomf//znqFQq+OlPfypUTDQaRTQaBQCsX79ekkjIA99555244447UKlUEIvFMDs7KxxuqVRCIBDA0NAQ+vr6pIB+Op1GIpHA4cOHW2pXECT19GRmM9IzZrlN6plZ04JJHrzenPVwO7o0r33Woxv3R/0zj0lXcOg0DL3jxeDt6/6WK6XMs4kHbed/j+Xxnmx9fq9TYD6eB9/1kE9spmku6+J05CHX63VMT09L9hmwxCv39PSIbCuXy2Hfvn3YtWuXFKEfHh5GIBCA0+mUKnCccgMQQGaBHAaRGLSiykDv6cb1KP/i1JgAvWbNGoTDYfzqr/4qPvrRj8Lv92Pnzp24+uqrkUwmEQwGkcvlEI1GYbFYsLCwgEqlgldeeQWPPfYY+vv7JYkilUrhkUceQTqdloJIFosFExMTyOfzuOOOO3D48GFpLAo0CwBVq1VcdNFFGBkZEd12NBpFJpNBJBIRLvcd73gHfvKTn8g50XMFIF4qK9WRF3a73XC5XEin0zKA6TQIgZCV3NoDOOzmwaCqzknrsjYWJNLVLwTodg+XXj2pjfZMPMriOAPSFRpnkrI4kTe52oCmnf9tB+XlAPXxzvdYAb52KuNY2ziZoqNry7OOg3osSm+xWKSp5cLCAmZnZ5FMJlGv1zE/P4+dO3fCYmm2fGKSRiQSkcBaoVAQiVs+nxevjbWS/X6/eOLcFyP3BDxOyenFNRoNKZDOEpBve9vb8NOf/hQDAwMCvj/4wQ+wZcsWWK1W7NmzB+FwGOvXr4fFYsHU1JSoFmZnZwWwtm7dir6+PkxPT+Po0aOwWq2IRqPYunUrent7sW3bNjz55JO48sor8cADDyAej2Pbtm0YGRmRUqSPPvpoS8W2SqWC7373u3jyySexZs0avOMd78CaNWvw27/921JFT6dtOMUnneB0OhEKhaRGCGcLkUhEvF29fCZpAlag6+vrExVGKBRqoRJ0/TP3TVUHBxb2KdQr6PFYWVmPgwSPh4ChGwef1ZY6vZqBpB1kTxawO9bfxwv06cuO5UWf7H/dVvM1XI3WcYF6llPUu0Y3Gs1qbEeOHEGhUMDk5CSA5o2ip+v3+xEMBltkW6yRoPffU0oJteHxeOD1egV82J6IQSzK4OhRskVTKBSSIkXPPPMM3v72t+Ohhx5qCRzt378fR44cwbXXXovZ2Vlks1lEIhGMjIyIJwdAAn5r1qzBo48+ivHxcTz33HOYm5uDy+XCV7/6VXzjG99ALBbD6OgoZmdnEQqFMDAwgKmpKXi9XjzxxBMwzWaHlEQiAZvNhttuuw3j4+OIx+PCyVssFuzfvx9333033v/+96Ner7cUZiLHy9kCPU9mLyqlMDQ0hPHxcWnwmkgkMD8/j4WFBQAQesnr9UphIwImM/o4E+E91z1dnYJoNBoyuKZSKXg8HqGdKGnU5X3H8uB0TzudTr/2J/o8sfZr2f55e6DueNs40efHozaO9X/XVsY6BmS+zHyRWPiGhWsSiQTy+bwUvAmHwwgGgzLlJnjr3CRfbp2jJDhzikzgB1qLFDHZwGKxSGo104b5++mnn8ZNN92EWq2GdDqNnTt3ioLh5z//OQYHB7F582bkcjkBJb/fjz/90z/Fz3/+czzyyCO4+eab8cEPfhB/9Ed/hJ07d+KjH/0oGo0G9u3bh+uuuw5vfvOb8dnPfhZ33HEHdu3ahfvuuw8ejwe/+MUv8KEPfUiuRzwex9TUFB566CFcfPHFuPHGG3HnnXdix44d2Lx5MwYGBjAxMYG7774bv/u7vyvepi5d07ngfD4vtI7X68Xo6CjGxsYknZzXncWeQqGQBOio3PD5fHKPmKDDwvvAUkozFS6BQACBQAA+nw+VSgXxeByzs7MAljqSM3BYrVZlcA0EAvIMUBYILKWVP//88yvwSJ8/djxJ2nKAsj341+5xn8gDP9Y6x+OTu5RFZ9Zx6jSj8Lr6Qa+9QG8rHA6LNpgFbbicAM6iQJyqskOF3otOz+wzDEM6XNB4s91uNwKBgAAQl5FXzmQymJ+fRzabxZo1a4S+oAdYrVYxPT2NVCqFdevWIZfLIZVK4cEHH0RfXx/GxsZQKBSwbds28WbtdjteeeUVvPLKKxgdHcXnP/95/OQnP8Gll16KmZkZDA4Oygvi9/uhVLNJLANqExMT+NrXvoYLL7wQk5OTeOqpp/Arv/Ir2L59O6LRKL75zW/i3//933HvvfdK0JKDGTP9QqEQAEhWJGcM7S+Ez+eDz+eTQKbVakWlUhGVDCvAsVIdg3L0jHVaQc/co+aYDQAAyCCt/3a5XFL7manp5XJZQPlMZemdS3YyAF4OD7wcz3c5nPTJ4gFdoD62nVK1N3po/M0Xl9Nor9eL/v5+9PT0oKenB3a7XTS03AZfRoK5vl3TNEVnS3mb3gOOnjE9N3rSNH1Krfdr09sh1Wo1oTWsViv+4z/+A29+85uRSqWQyWRQLpfxhS98AYFAAJlMBh/96EfF4/vwhz8MoAkijz32GDweD770pS/hrW99K2w2G77+9a9jcnIS/f39sNvtmJychGEY6O3tlWm6y+XC8PAwarUajh49ing8jvHxcezbt0+ol76+Plx22WVYu3YtvvGNb8jsgvUsPvWpT8Hr9eJrX/sayuWydHkOh8PweDzCz1NFQkDmYFgsFoUm4IyEKe8zMzMtxet5zXT6gQHJQqEAwzCQzWYFuPXAnj6gAhBPnwXyaWeb7O1sspOB7LEChbSTecvH29bJgorHA+XzGaw71iEbhiFtfZLJJBKJhLzU9K7Y7JQZffyMHlij0SwgzzZEeuRdV16QI7XZbIjFYshmsy1KAr2uAr09qgTolTkcDhSLRXg8HrjdbsTjcQEWggclcTt37sSaNWvQ398v1dAIHuyozOOlp8l2Tf39/fj+97+PLVu2oFarYXh4GHNzcy18OD1xqhvIsZMmmZ+fR6VSwfe+9z14vV5cccUV2LZtGwKBAL797W+jWq1ieHgYHo9H0roB4DOf+QxqtRruu+8+/OhHP4JhGJiYmBAJYqVSQW9vbwtnz8zCYrGI6elpZDIZuT/pdFqkdxz8Go1mY9J6vQ7DMBCPx9Hf349Go9m2aXp6GuVyGel0uqW2MV/GcDiMvr4+2f+hQ4eEP6d6Q5/5dG1l7VRB7mSa5xNt83gA3im3fT4BdMeyNwazqGIAIKoB8sEMwul6Vh1EOSXWu4rowT56kfX6Ulsg7p+1L5hirE+n4/G4dKemlIvb1cta0lum8iAYDEqQ0W63Y/fu3bjgggskK48BRwbGlFrqO+fxeCR1mpmCVJe8+OKL8Hg8iEajomLgMehtsMgPs/YFs+t27tyJp556Cu985zulZseRI0fk3HK5HAYHB2UW8Wu/9mvYvHkz7rzzTszMzMj18fl8KBaLyOfzMmPQO1/Ts9b5fF0qx4ApB8pqtYqJiQkBfVIovEdM+6ZEr9Fo9s/LZrOiYSZdRa9Yp1m6dnrsVIBtuWqKU93mcr9/voByx4B88OBBDA4OIhAIIBQKCfdKfTBpCXZI1msfeL1eyd7iy8rymARlrk+1BIGLU2pWhuPxkJO2WCyYn58XQKN3aLFYYBiG9KrTM+MIMIZhwOVyIRKJYGFhAaOjozh06BDGxsYwPDwsNSAI0KwIRw96w4YNWFhYQKPREH5537592Lx5MxYWFmCz2TA3Nydest5JhLI+PmyJREIGC5vNhmKxiB/96EfYv38/br31VhkMmCnJ+suHDh0SpQMDfbzu7ApNiofXrVgsymBApQuPh7pmt9st4MxrzQGQ9400kz6jYNCX4AwsUUuksEh36brkrq2cHY8P7gTc2oN/+vorcb9O5oGfb9ZRpp7b7TbHx8fhdDqxdetWCdDs3btXOmyQnujr65OEEXq4BNV4PI5UKoV9+/YBWCp+Tm+J/7MOBKe56XRaOEtdmsapPwOMLDZEWV4sFmspdENQ1o38KgGip6cHpmnCMAzs3bsXo6Oj2LRpE9xuN2KxGHK5HGq1GkZGRjA1NQWfz4fLLrsMc3NzUvSe3qDX60Uul0MmkxHveWBgAH6/X/r2pdNpHD16FOl0WgYpq9UqAElgu+6667Bjxw643W4YhoH7779f6BfDMDA3N4d8Po+hoSH4/X6EQiGkUimhN4BmOdBoNCpet2EYSCaT0smFAT5gqbGAngqdSCTkRdKTRPTkDoJwsVhs6Yyta8Y5aLJ5QDQaRaVSOSOZeq/3Ps+0LTdD70TLVtJrXc62zmYv+bRk6jExhNNfvtCRSAS5XE5AkiUegaX2QzQCEL1SBtmUUsIz0+PVQZf8p1JKov06PaJXDKvXm73xmNHHIje6t9auj2WyhV7gKJlMYmxsDNdddx1sNhsefPBBXHLJJZIkMTs7i0AggFKphGuvvRb79u3D2NiYlOlMpVLo6elBLBaD2+2WuhM+n09Aj8fLbinAUuo3p/QEZKUUHn/8cdx333344z/+YwwMDOBDH/oQfvazn0mXax770NCQNHYdGxuThJBisYjZ2Vm5l1S/sN4Gg3Wc3XC6yKBhLBZDMBiUBCG9sBQBmfebVe/Yqov3j1YqlZDL5ZBMJlGpVJBIJDp5HLu2DDseiB0r8HYsFUb790/22anacoJ7ZysYd2IdATJbFqVSKczPzyMYDEIphXA4jHQ6LVxmvV5HOp0WPTL1wLVaTbK7yFMyBVuvWUEviq2i9OI4DEgxGKZ7cgAkos9pNafNlGbR42xvBmqz2bB7925cccUVOHToENatW4ehoSHE43EcPXoU4+PjuOKKKyQbMJPJYHBwEPl8Htdffz0OHjyINWvWCLjPzc0hHA5L8C4cDst0vlAoSHCyp6cHxWJRfuhB6xlxHHhICY2NjeGee+6RUpdveMMbMDQ0JN216/U6RkZG4Pf7hZpgr798Pg+llGiSOSgQiHm/dI+Wg2w0GoXX60UymRQNcyQSEfDm9eQzkEgkJFuvt7e3RZbHxJFKpSKzhyNHjqzAI9013Y7n0R5Ps9zO13aVEK+vnVKmHjt4lMtleDwe4ULJZ+rgyQwyelL0CAEIT+p0OiXDix0/ALQUDmIwrz1ACKAFlAks5LH1Nkf8ju4ZE+gASAH54eFhPPHEE+jt7cXY2Bi2b98u/ffIPRcKBQwODsLr9WJ+fh5DQ0MoFArS2opF759++mkMDw8jFothx44d+Nd//VdYLEs9/nQVh14dTb/meh2IYrEo3nKj0RD1iFJLWudGo9GSdk7elkAbDAalQzaDk0zoYPF8cvecOTAISDmb0+mUOAIHD95jnYPmAEqVBwOJVFeUSiV4vV4ZHLp2euxE+mMu1z3kTpQQpwucz0fA71iHDEA6dGQyGUkw4Mumfw+AJDBQXcEMM4KOy+WC1+tFMBiUWhYsiE7vjMXO6TnT4yyXyy2F8QEI90ojt6kDEsGN6+g95GKxGMbHxzE8PIz+/n7U63W88MILGBoaQiqVgtVqRT6fx+bNm2UmMDQ0hFKpBJ/PJ4FHh8OBXbt24bLLLoNhGPD5fMjn8/B4PDAMQ9QNnCE0Gg2p7kbv0+FwIBQKyayCdUB43OSxmaLM66zXjeb94X2ht6t73HrtCj1RRKeJmO1HfTjvWXv3cfYlJJfPAB6bFBDYeUz64Khvp2srayeTrp2IGjhT/O756IV3VM2Figo2DI3FYojH4ygUCqIhpkdK8NSLy3AE1r1kYCnJwOPxwGq1IhwOS7Ydp7OUeTEdGGiWz9RHdAACTARfnd7gg6drn/VjWL9+PUKhEA4fPgybzYZUKoVyuSyNS7du3QqHw4Genh7UajXMzc2JZG5hYUF0vKbZLI95+eWXyyB1+PBhJBIJXHfddTBNE5lMRpIpYrGYVGxj3YpsNotgMIhwOAy/3y9BOQYegaXGsNlsVjxO8uAsjUnlAwOMehIOBysqLQjsulyR10Yvfu/xeOD3+wVkOSNi4g61z5xNkD7SO5twdsDt0hPv2ukz3VFqD9KdKKB3IjBfScVF105B9sauGswaY7YdJWb6S0yZk/6S6y83AJFP6UoC6oEZ6OKLy6QD8s96iUhKufSyjvpUnbQEv99eohJYGpGpq+a0nWU0Z2ZmJImk0WhgfHwc+XwegUAA4+PjqNfrUnuZg1IikZBBizI4i8UiHUpYi1hXKbRPBwG0JLIQaHWPU6/1wetKLp0BQtaX4HXQq85RhcL6JFRBMIBKSoX/s/QnwZx6bc5uGNjl7EQfRPQBgDOmrp1+O54XfKxnrhMO+URgvlLHe75Yx5QFXx626mEgTyklkXpdyUDNMae+ehdjPdGALzv5UJfLBcMwUC6XW8pHlkol9Pf3t/CfTKjQPQAmhPB4yEHrU2VynQRvAPD7/ejv7xeP7qWXXkIgEEBfXx+sVivm5+fR39+PcrmMvr4+FItFHD58GBdccAGi0SgikQgSiQT8fj9eeOEFBINBjC9WiJuenoZSCtdffz0effRR8Yg5WJDWoRFsbTYb8vk8EomEXE9qsW02W0ujUL0LB3lcgjeTNeglswYyaQgWAgqFQsIJ6+oTgigHJAByvKRbuM9yuYxMJiMzBs5I6EFz1lMsFqXOxfmoO329bTkAuxxlQ3vwr2srYx0BstvtxqZNm4TPJSWgy8l0IKD3SZDQe/HZbDZkMhlJO+7t7ZWyntQVA019sJ4FZpom+vr6JEhUKpXg8XgkeKhvH1gqWFQqlSRwSDpDL14ELE3NWWD/13/916W28Pz8vJS6zOVyQiE4HA5s2LBBlpNSqdVq2LBhg5QA3bRpE4aGhvDwww/DarVi48aNLedns9nQ19fXkjoeCASk0SqvZzweb1Fi6JXf+ILweusBPf2eGIYhrbY4YPH/dDr9qheNKhfqwxksJNCSd+b1bO8owiQaoAncTLVmKnx/fz/cbvepPcFdO6kdD2zblx1rPdqJ1uuC8spZx4B8wQUXSHIGax17PB6pc8GaEvRg9Qai5Ciph9XrUkQiEfT09EjA0DAM8aoJ9lRZBEXoWgsAACAASURBVAIBBINBCbAx2EQKQk9AoIa2XC5LogVTrwFIAR7TNEUlUK1W4XQ68aMf/QgXXXSRcMLkjt1ut4BOPB6Hy+XCG9/4RhQKBQQCARw5cgS5XA52ux1+vx8bN26Ey+XCE088gS1btiAUCmFkZKQlkUKX8ZFa4HTf6/XK9Q0GgygUCtIpmgE6Ug26uoFpzDxXvkSBQABTU1NyX1nUfn5+XuqSkCNmRiUpJ6oheK0AiLwwkUjIsegctj5YMGuQzwQ7yuiJK11bWTsR/XAiMF0OULd/3gXn12YdAbLdbpfaCQRUr9cLANIDjl4UAz9UCDidTlEFEGSpOKDczev1ClhzOflfXaJGoAeWavSy/ZPusevqCZ0z5g+n7azFwPVvvPFGfP3rX8fatWsxNzcHm82GwcFBkagBkMSQTZs2CX/tcrlw+PBhAe/BwUHE43Hs2bMHQ0NDeNvb3galFJLJJC6++GLhVYElvlpXSZAe4CDF9GdWTdM9YnLlVqsVTqezpdEp637wRXI4HFizZg2mp6cBNKmSUCgk6g995sNAJaWL1Cdz26QiOLCxmwuTXVj+VG9A4PF4pAogPXK9rkXXTo91ApYnA9dTUWJ07eTWESDTCI4MHJGDnJ+fRyKRkMJDlE3xReN6jPqzCwb77Hm9XvFumbVHkKLnyuk8Oc9cLgfDMMSj5rq6lre9fxsDhwQTAonON2cyGWmUumHDBvHuSKtkMhmhDWKxmGhpTdPEyMiIFNJ58cUXcc0112BiYgKTk5PIZrMYGRkRnlyX/7FrN4NpTOIghUOulQMeZwymacpMRQdiPaiqR8L1VHVSDjweboeBPW4PQEvAVS+xSaojmUxKkFePwHPGode+9ng8MnuhHrnLIa8OOxVwPVkQsGvLs45VFqQlOCWmZ5xOp3HgwAEUi0VREnAqyxRmRvbj8bisHw6HUSgUEI/HZR/s+ebz+aQMJnlRBoXopbMuhl6sh0BEANenzADE62Y68OHDh7GwsCD1mwcGBtDf3w+gWTbSMAyEw2GMjo4KlUANLqVedrsdyWQSgUBASmPm83lcfvnl4u1y8Gk0Gvi3f/s3CUpef/314rWzqho90nK5LAFGBkQjkYikrdPr5ADICne8lgBawLk96MpBiqDPQkJUYFDrbbFYZBAkvVAoFGQwm52dlRofutSNAypLkPL+sPoe6SQO8F07vXayBJHl2LECeqdLaXG+WUeArNfX1TPLyOEODAxIKixfNBY518tlUmerJx6k02nx1Pr6+lq6WPAFJ6DHYjEpIp9OpwUYhoaGWnrNcepPnS6BnTSAznWyRjOVD+94xzvw6U9/GhdeeCFeeukllEolbNq0SZJDqNgIBAKIRCI4ePAghoaG4Ha7MT4+LjUrDMPA9PQ0+vr68Pjjj+Pqq6/G0aNHpZ1ROBzG3/7t3+LWW2+VxBkALQDKa87MRvY11AEZQIvXSoAjncBgqf6jB0C5Dj3jfD6PXC4nnVj03n7MFsxkMsjlclLbmt4uwZwcNwdHBvwI7lTQsBSrLofs2umx5QDmqX7nZOqNrp3cOpa9EeToJdNjttvtknYbDAZbgj580Qh8bIrJbDV60Qz46aDEl5r943K5HBYWFhCNRqWSGHnnXC4nCQlcl149p9LMAGR3a2YZ9vf3I5vNSkCR0jW3243R0VH4fD4sLCwgFAqJ9C2fz0sBIkq9GDz0+/2Ix+PweDx47rnncMUVV+D6669HMplEOBxGPp/HwMAAJicnEQgEcP/996NSqeDmm2/G0NBQi4qBFA+5cp1LJ41AsKNHTa+XlfH4Pwcc6pPJWesSOXqwvDaULRLYGQQtFotIJpNYWFhAsVh81bXnLAmALKMyht2w6UXr9Za79vqYni59qqC53BTrLjAvzzrmkPWMLba0p7fL+glMd9ZTcum5sS3T3NycaJiBZlSfCga2GeIAQK+M7YgymQySyaQU02HNXrYfikQiLR4hs9FIseieGnlUPVOQ0/ZPfvKT+OIXv4iRkRHR0DYaDVx44YV4+eWXhZ9l1h1bNpEmmZiYwMGDB/HWt74V6XQaExMT0sHE7/cjGo1KgSbSFD/5yU/g8/mQy+Vw2223tQxOvO6sjEZAZvCTNACvdSaTgcvlelV9DAAt50mpIgODehYf6Qa3290indPpBQIv6Q92bNEB2GKxCM1isVikKSqfIx7DuWarGYh02VonlMOpSN5W6zVYbXZKQT0G6ejp0BOkFI41KYClspkMBHEden58CRnwCYfD6OnpeVWaLTlk/s11dUBvNBrigRIs9RRp/W+95CW9Rf38lFLI5XISgGOtjYmJCczOzmLjxo2SkMJSoolEQmiLhx56CH6/H9dddx1cLhd6enpgGIbUJqZ0Tpf+se4EKYp77rkHV155ZUvtDQ4mAERHDECuLzXbTB4hv83gHYCWDEbST+w/CEDoHf0looSPskaqU+RBWtwW981gIL1u1ujgoM17wGvNwfFcs9WcQHEqwLpSgdfVek3OtHUMyAQ1wzBE4ZBKpTA3NyecJAM4/f39GB4ebikyn0qlZDqsT3VYrvHll1+Gy+XCwMCAcMj0qguFgvCWzExjhTImbBiGId076KXpHHT78VPfa7VapQgOwUUphbGxMRw8eFAqqG3btk36zimlRG9NT3lubg6HDh3CZZddJoAYCATw4osvyvGSV2dQTy9RSj7X5/OhXq/jySefxKZNm2TAoP6ZdT3ojbNUJ5NgAEjNau6T3qkOgqSeqNjQ77Ouk2aQUZfQ6dx1ezsmna7gLMflcglVFAgEkEwmhWPWvbRzzVYj8CwnY+9Yn7/Wc1mp7Zyrdkpdp8mzcqrOqTzBjnI4AgO7ZjAIl8lkXiXP4vbT6TSmp6cxOjoqNAK9ajYU5X7Jp+rSuGQyKWDLJAYdkKlWyGazSKfTUseZcrlwOCweosfjwbp163DkyBG8+OKLuPDCC9Hb2yu0w2OPPYZLLrlEqJhnn30W27dvRyAQQCqVwvDwMAzDwJ49e7BhwwbMzs5Ke6V0Og2PxyPpzpTQ1Wo1fO5zn8OXv/xlmc5PTEwgn8/jwgsvhMvlainmRH0yCzvpldQoC+R1pOmqD947YMnL1uti8NyYTagb7zV/sw0U96EH7xiUZH3oSCSCWCwm3v/5YK/VKzwdXmX7Nts533YAfa3H0AXiE1vHgEyedn5+HvPz8+JdAWjhZMklTk1NCZVhmibi8bi0fm+XXdGmpqYkaYS94wqFAqLRKKLRKOLxuLzoMzMzsFqtCAQC4rlOTU1hYGAAmzZtQiAQkCl7qVRCJpNBKpUS3Sw9TvKdqVQKuVwOxWIR/f39kq32vve9Dy+88II0NKW3XCwW8cgjj+Cqq67Cli1b0Gg0MDAwgJ6eHuzfvx+9vb2S3ej3+1sKCTGJQu+ObbfbcccddwCANEO97bbbxHsdGRnB5OQkvF4vHn74YTzxxBPCn+/YsQNPP/20AF+93mxfxQFGb1zKICjVDRys9ESaSqUiBZ3y+bzopNmFhbw8BwaqYMhzA61V3XK5nGQYsrUXB2uXyyXPxblqr4W+WIkAXPux6L9PtLyd2jgdEjf9/PRtnw3UxkoeY8eAnE6nEYvFkM1mpYsx6YF2LSmDVYlEQvhR3TPWQZjJCgSEV155RQr4MOFhfn5eKqdx3dnZWSlVyWSKSqUiQSOCo1IKhmEgFothYWEB2WxWLqTeEFQpJVNpwzAwNjYmwHzhhRdifn4e2WwWv/zlL5HP5xEOh7F+/XrR8QKQrh1MKCHXzeakVKZYLBZJVU4mk/D7/firv/orfOYznxFN8q233grDMGCxWNDf3y+9C/P5PN70pjdhx44d+NznPof+/n489NBDGB4exiWXXIIHH3xQsg9ZjU+Xo5HKoWfNgCrbS9FzJ0/ORBjSHlR+MA1aB2cCPBUd5KhZAc9msyESiSASicDpdKKvrw8ul0u06OeyneqL2ynXuxw7FpAcCxjbv/NaBpTj7fd453c2APNKHlfHOmTSAeRQ9eI8fOH0Epd6yUc9UYE3nOsQsHRPLpfLQSklEX5yx/pDY5rN2sIs+0gawzRNLCwsSOCJBdYNwxCvkMt0uRd/KBfzeDwIh8OIRqMolUqYmZnBiy++iF27duHP/uzPRJdMyuSJJ55ANpuVJqYMsgGQBBW32y2qDWa+0Ru99dZbpUHrBz7wAdEz5/N5xONxUZ4wEBmLxfCVr3wFX/nKV2CaJiYmJjAxMQGv14trrrkGe/bskWtOSkQ3XSPMzEgCMtUSOuhyOQFW5+ZpekcQ/s/ZFYO3TN+2Wq0YGRmBy+XC7t27O3kcu3YaTQeZlUgmea3rr2ZgPlaSzKke4ynVQ2Yyht6XjkADNIGHHal14AQgXrQui9IP3mazobe3V+Rz5I9JR5CXbm/DpPOmBFjTNBGNRlGr1UTnms1mZR3WWeD+CUIMoDF9ulqt4gc/+AHGx8dxzz33YO/evfjWt76FVCoFr9eLiYkJjI+PAwAuuugiJBIJuFwuFItF6UBdq9Xg9/tF/UAaQU9OYW2LiYkJfPjDH5bedQ6HA729vZibm4NpNrulECi9Xi8qlQpuuukm3HfffQLuiUQCP/zhD/G+970Pu3fvxtq1a6W6GgNuelp1MpmUc2XHEgI0FRV6kSL+6OCrlzzVB2muQ36ftTl6enoQDAYxMjICt9vdonTp2um3dk/4eECiLztVvv9UAfV4HPepbOt02UrMIGgdqyzawYTACizJqVgARwdG/WDJ2bIgEOkEZtEBSy8yPWzykHohen377RI3Ai6zBVmsndNp/q3XtdDXIcWSzWbhdrtxzTXXwGKxoFAo4MCBAzh69Ci8Xi8ajQY2bNiATCaDF198ERdddJGUy2TXaW6fHqdeAIg1g3ldFhYWMDQ0hFwuJwWZSHkMDAzg8OHDUsiIL0i5XMbY2BgACDiSV15YWMDBgwcRjUaxdetWhEIhjI+P48iRI1L4SS8nqgdJAUjgkfsiFQEseU66GoOf04PmtTZNE6lUSor8UxnC5Bs9kahrr5+dDDyORTW8FiDsdL0Tff9Yx3Uq+1hN1jGHzKLpOoDp3aJpegEagh6B1G63S/85AqnT6RT1gFIKvb29ElhyOBwtNRK4T96AdsDQwRaABJ14vJy2s5+cXv2NRnqBheGHhoZw++2345//+Z8xMzMjkjXSLeFwGG9+85tbtnvo0CEAELAJhUKSoch9eb1elEolSTQZHh7G7Ows7r33Xlx99dUIBAKYm5sT1Yjb7cbk5CSGh4eFo/V6vdKto1arIZvNyj3gMWQyGTz++OMYHh6GzWbDSy+9hKuvvho333wz7rrrLsnIYyyA1+9YRYb4LPCa09PW2zbpnjGwNBA//fTTGBkZQSgUwuDgIAB0iwutAjuRd6z/Xs46K30MJ/tu++/V4jmfinXcddrn8wkFwBeWF4BTXWbGUQbF5bqaglIvboff54UkNeHxeETxoLclohdHQACWptIESg4EOrXCIBaBVO/YwW20Byd9Ph8+9KEP4e677xZtr8VikTKYLC/Ka0SgBIBnnnkGbrcbg4ODkjDBpJBKpYKjR48ikUgIqCWTSYRCIQDA448/DrvdjlAohI0bN6Kvrw9jY2N47LHHsGfPHoTDYbzlLW/Bv/zLv0jJUl5XeraRSATPPfecDIixWEyK5D/22GP4wQ9+gJtuugl2ux3z8/O49NJLsWfPHsnw42Cmd/4g4LJ7CWtdcBmviV5Lg9cGaA3gchbSPiB27fWxdlnbqa6/3M/15cCJvdlTBdbjOQ4n299qMNWJVxKJRMyrrrpKaAtdQ0y9r57tpUuogFdHbAniSikBYJpOSehBQFIl3Ce3w2V6oJEeuH6cuvfW3viUv3nM9LaVaiaI/PVf/7Wcm9PpRDAYxNatWxEOh+Hz+eQ4K5WKJMBMTU3hyJEjLZ4kZwCxWEzUGe375TWwWCz4kz/5E3znO99BpVIRbr23t1daTPn9fulGrWcvMhHD5/NJMSXWr+DxUnr2sY99DLlcTqiadevW4ac//akMfpwV6QE8prK3pz7r9Sx0Gon3iN44OXUmxvzN3/wN5v//9q42to0qaz/j2I6TsR1/x05S0rRURUW0Kl8FtEu3VGxZipRSqUWFSC0fP5AAUQkoCFVCQuIHiM+FXalaVdrVigI/0IofUMG2y0KBCihSKaKkIm2TuInjOLYTe+zx97w/vOfkenDaJG1S8zKPhFI8npl773iee+5zzj1nbGzR3xhJkn6zpvl8SW++RDyXa1wKEm0Ua1nTtFk1Yk6E7Pf7td7e3l941cUOi/ouEZz+O/oB0i9/RfKlz4m0ZjpP/Ev31UdP6PVsam89xwb9paV7JBLB6tWrsWLFipqMa7QNmHaxaZqGffv2IRwOc76NkydPstzS3NwMt9uNQqGARCKBUCiE7du3Q1EU7N+/H5VKhesV5vN5bNmyBd3d3exwEycdajdJONQHcXKz2WwYHx/HJ598AkVReFej1+vlkLj29naEw2EsW7YMg4OD2LdvH8djx2IxnDhxgu8jrkjqkbD4bKg9YnSN+BsQVy8AcODAAUSjUYOQFwlzIbzZEJv+3Tqf3nwpiHKuhF1PD18sLAghBwIBbfv27dMnS9NhYqJmKxKrmLWMBkHMzUDfn8lTqT8mSh6ihat37ukng/N5Z0WrVNOmcz6QtZlIJPDkk0/yzj4qxCpmWyOnGG0T7u3txZIlS5DL5dDf38/X37NnD4eP6XNGULa7l156CaVSCU8//XRNlWj6S+NMf0XrWt8n/Y+2Uqng3XffhcPhgCzLyGQyHEq4YcMGFItFTExMwGKxYNWqVdiwYQMOHTpUs+LQO/DEZyB+rv9/ageNsbgC0TQN7733HsbHxw1CXiTMxwK9VER6qcmw3jVnMtguh9W8IITc3t6u7dixo3qizuIV41bFF42gly/019CTOEEf26w/V7TMRCtaLz/oiUSMyhDJRJRXbDYbzGYzHnzwQXzxxRdobW3loqSksQJgBx/pqNlsFsPDw3j44Ye5eGh3dze2bt3KIWdkTdcbB3Hs9ESsJz4R4viKEoxIfmIfs9ksDh48iCVLluCbb76ByWTCW2+9xeGKhw8fxnPPPYfBwUF8+umnNc/xfD9qkYzFPorOF71eLEkS3nnnHcNCXiRcLCldTnK7GFyuds+WkOcc9ia+VCLImqxnqdFLKS5PRYuLzhUtbT2Z0/dIvtBfn44TOWqaVvNvOodCzIBpDVmUWcTrlkolbN26Ff39/bzEpgdJCfUpdCyTyfDWYUVR8MMPP7AF/Oyzz/IYUd+pj+L41LN49VamGGJIPyxRE6e+0LXpPHHCo7GQZRn33HMPyyMAcOjQIfh8Png8HmzZsgXj4+OcJIpyT4irCbHNIhGLkTCzmfTnYhgYuHhcLCnNxAONhpmkVfF4I/Vh3jX1CPrlJ4AZLWHatEGbQfSSBlCrQYvyAYCamGfxu5I0XStP3IEH1O7Co7YQEYvkJNbYI7KrVCoYGBgAULWCxZ114i7EyclJ/lsqlTA8PIzXXnsN69atw2233cZtpXHSSyhi28SJStTDRegJVu80FS3/mZ4dTXI01ps2bQIAHDx4ECMjI1ixYgVHsqRSKQQCAa4qLY6v+Cw0TavRi0WypnbrNX7x+TfSi/FbwHzH+9f0rPQTT6NPJPO2kEmiEHPs6pfL4vKAyFW0CukFFolQJBrRatWTEoVJ6Zf3RJT1dgGKzi/R0qRz6Lo0uTQ1NeHLL7/Epk2bUC6XYbPZeMNGc3MzXn31VY6Tvvbaa+HxeHDq1Cn84x//wPPPP19TQQNAzTKd2j+Tdk5tEyMv6mm14v+L4y2OJY2j2De9tUyri40bNyIcDuP777/nVKbLly/H2NhY3VWRfvOP3qqv1ydgWuaptxIwsDiYC7HWI7VfC87nq2o0zCsfMr3QeiLkiwoWsChHANMvpGhNA9PWHcWt0vfEDQl664o+o3NE8tY0rSaWmNpFn4nRAdQevWyhadWQr5GREQQCAaTTaQDVwp+vvPIKxzDHYjEcOXIE6XQaf/zjH/H0009zHC7FWIsrCbPZzGGBojVLx8Xlv0iy4u63SqWaVS6ZTKJSqfB2ZLEvIlmLlrZeWyZQ3o0lS5agp6cHU1NTOHXqFOdnFuUdkUj1lq9o6YvtoPuJk4U4YRtYPDQ6Oc3H4Xgh6Im5EcdgXiWcJEninW9k6ZE2K1pf4ssmkirV4COy1UcOiBaqPoaVvkMkR9ck/ZlIRa9Ha9p0Skg6RjG4ejIQLU6LxYKvvvoKTqcTPT09cLvd2L9/P5qamjg6wev1olQqweVy4bvvvkMwGERnZyf3m1KREkGT85MmDXGS07eDrFhJkpDP57Fu3TqoqorbbruNiXjv3r147rnn4Pf7sWfPHt7STc9LH64GVCcicbLT69dANZRv9erVPImJDkZxnMrlMlva1GdxcqPnIG4amWmyMLA4mCshLQaB6XlioaSsRrb05xVlUS9iQr+kJiIh5xgw7XSiZOdERvVIQYxjFjVVIgwiVH0FC9r9RefTRgfRyUVShz5ETtRvAdRs2CgUChgYGEAkEuH8vZFIBD09PUilUjUbYmjS+v3vf899E2vU6a15kk1EghS3hhORtbe34/XXX8e6devQ2tqKF198EZJUDb/L5XJcleWVV17hsaexIWtelGqoXfRvapv+2Wqaxqk8K5Xpqtb5fJ4zv4m/CZrwgFqyFfOQ1OvfgQMHjI0hi4xGsxbP145GaeN8oC1ElAWRlVgHjgZJDOXSb1QQrV9N03gzBZGSWDJJfGEJdG06Juq9/+tsjYQiFvYk61K/dKZ26nM3UJtJU6XzLBYL1q5di6NHj8Lv96NcLnM+hlgsxsRGNQVLpRKOHj2KW2+9tYZwKTSOrFZqnziu+mV9sVjExo0bsWLFCnz88cf405/+hFtvvRWapnG6UUmSsHnzZqiqiv/+97944403eIs4jb3o4CSLVdTURU3ZZKqmyFQUhbevA+DdmCaTiTPXkaNWjGAhwhV1azEkklYnYvrRX+vL9mtGI1iLs5kUfs1kPBfMmZAp9wRZeWT9UJ4GSqxDRKOvRiFJ1dpsVEEjn88z6VCVC5GQy+UyZFnmhPJE5q2trZwAiEhOtM7Fl5+Ila5nt9s5zAuo5s2gLHNkVVPbRbI2mUx47LHH8Pe//x1TU1PQNA1HjhzhQq50Lv1nNpvx+eef4/bbb4fNZuOcDWQtU9kmIjtqH7WDxtFisaC/vx+KouDVV1/lIrLlchl9fX2Ix+NYu3Yt7rjjDvzrX/9CNpvFxMQEV1GhDSx6B6BIwOKKBgB27dpVE7b217/+FU1NTbjzzjtx5ZVXciXpffv28YRAqxGSowCwPCMep/vRyokmMkNHbgwsNvk10qRwuTHnfIeiBSxJEudAJlIiMtQTmVjmCahat7TFl6pRmM1mTk0pJpuhahaU1tJsNnMIGll9VEuOyE5MCUnkS1YnJfah79EkQpMB1ZoTq1xT1Q1N03D33XcjmUxydjoqLFoqlTidqFi49N///jc+++wz1r7pe5RWVEyiT5Mc9Z3klw0bNqCrq4vTlMZiMWzevBlPPPEEnnrqKbjdboyOjmL9+vVoamrCww8/zNfTy0ZUgol0dbGSN5XGevvtt2s08N7eXuTzeXzwwQc8ZlRgls4vFApwu90AgFAoxM+R4rGp0gnVMBRr+Bm4/KjnS7nQJHmpJtF61xEd25fqfjP5i/RkPNNYLLTRMCdCpqUmlaovl8uc95jIhTKyEcSMX0R4RBIkJTgcDkiSxC+upmlMPGKkhhiNQCQpyhekp4qESJs3SEqgyYKsZzF0jjRWIncxrI9WBlSk9IknnsCuXbs4IQ+NRSaTQTKZRCqVQrlcRigUwr333oumpiYcPXoUN998MxcmpcmBtHSyoEWno6qqWLVqFc6cOYNkMom77roL2WwWqVQKN910E/bu3YuffvoJjz76KF544QXs2bOHLWHqB+WDTqfTNaWrgOpkRRNLpVJhZ2k0GuWxKRaL6Orq4uOiY/e+++5DuVzGnXfeCZ/Ph97eXmQyGVxzzTX4wx/+gJUrV+KWW27BDTfcAJ/Ph87OTmzcuBE9PT3QNA2bN2/+ReSNgcsDPSnRygeYmTDFVddcIZ4n3lv/udiOi7Vi6/Vxtt8TfWR6XKrf7pycep2dndq2bdvYQiINk7RYTauWd4/H40xmbrcbyWQSAJh4qYP08pNWSsRNFjFZVZpW3UlGeYXJwlQUBTabjUPMKOk7abgUhUDXbG5uhqqqvLuOdE9RNyWLjaz6QqFQY4lXKtXkP2NjYwgEApAkCadPn8ZHH30Er9eLVCrF7ejq6sLtt9+Ojo4OlmU6OzsRjUYxMjLCk8Tk5CQcDgdUVUVbWxvS6TQv9ROJBG688UbkcjlceeWVSKVSePzxx/Hhhx/WyCO0UqEJKh6P45133mHipGOyLPPEQpMNab+iNpxKpbB06VL09vby8yZn4a5du/hZapqGt956C7lcjjVlcv6RLiw6HmmM7XY7pwyl7xlOvcbCQjv8ZrJOFxoz9edCGjZhpnNnOva/45c+l0VXV5e2fft2NDc3Q5ZlFItFuFwuSJKEZDIJs9kMv9+PfD7P22w7OjqQSqW4TJHP50OlUoHL5UKpVOKcwsViEcPDw3C73QgGg6zJJpNJJBIJOJ1OAFVLNZlMoq2tjUnNYrGgpaUFiUSCrVXavCFa51arFa2trchms5yrWdxe7XQ6US6XmSiIFAuFApxOJ9LpNGw2G+veRPiqqvK1X375ZaTTaaxevRq33HILli9fjpaWFk5PGo1GWV/dtGkTPvroIwDTOmo2m+UUm2S1u91uvPnmm4hGo/jb3/4Gp9OJY8eOYfPmzSwbiXr+jh074PV6sWrVKs7oRvcgEqY+ZbNZtLa2IpfLsfUvhhXu3r2bSfXbb7/F8ePHYTabsXPn2hSB5wAACRlJREFUTv7xTUxM4MCBAygWi0y0olwlOmsBcFkor9fLBWUlScLbb7/dMLksZvGCzYtI9OfVe/9mc91611kMYpsPmTU6Ztuni+njgkRZkONNURSYzWakUilMTU3VWDlU9NPhcGBychITExNIJBIolUoIBAIYGRlBqVTCmTNnuNoFkRFZiYODg4jH45zIR0zo7nK5EIvFOMzL6XRidHQU6XS6pnIGSSqkka5ZswZnz55FOBxmwunu7uacFJVKBeFwGNlsFn6/n5fwHo8HiUQCsVgMra2tnHpzcnKS8/r6fD6uKvKXv/wFklQtSSXLMtxuNyRJgqqq0DQNV1xxBVRVRWdnJywWC9avX4+PP/64ZjmkqmoNOReLRQwODvJqIpVKYe3atUilUrBardi5cyf+/Oc/w+l0wmw2Y3JyEkuWLGFylCQJbW1tXONP0zQ4HA7E43G+D+nrNOZiVAY9n+uuuw6apuHw4cPslLNarfB4PLwyymaz2LBhA44ePcqVu6n6CwCMjY1BlmUeQ1qhLIY+Nxdc6MWb74s52yXzbK9DJDEXq03/+YXGXTxff9+LJejZWKULPfHM1I+FXB3M2Ja5vAR+v1/btm0bvF4vFwAlRw05eOLxOFcCkWUZLS0tiEQiXKz0qquuQjQa5U7S0pesYCo/RFEPpBV3dHRgbGwMNpsNiqLAbrdzJAWRjaqq7OEnyzCVSmHFihUYHBxEoVDgJTkwvVSnoqwku6iqyonzFUWB3+/H+Pg4Oy1lWUYkEoHT6UShUMDvfvc7LF26FN3d3RgbG+MySldffTUGBgY4isPlciEUCuGbb77B4OAg8vk8wuEwvF4vgsEg0uk0Ojo6kEwm0dHRwVZ1sVjEQw89hGeeeQYmkwl+vx92ux2VSgW7d+9GMBjE+vXr0dfXB1VV0dfXh23btnEOZbfbjVQqBafTyUmQqO+qqiIYDEJVVTidTibjQqGAqakptLW14f777wcA3mFYLpfxz3/+Ezt37uTJTYwy2b9/P/8+RB+Cqqpob29HOp3G0qXVun6Uj/ncuXN47733MDIy0hAWsoFfpkydiaD0x86nDc/FEp2JkPWfzbdvi0m0C2IhU+n2eDyOyclJ+Hw+JjGv14toNMrkRg4kWZZht9ths9lQKBQwMjLCFYZTqRRbsjabjdNdjo6Ooq2tDfF4HEB1x9jk5CSsVitXeibrsVAoYHx8HB6Ph4uTUlidoiicCtPtduP06dNsRedyOXZmybLM1/D5fEin01AUBS0tLbDb7fxdclg2NzfD5/Ph7NmzCAQCXIrp2LFjvEPv+PHjGBsbY8356quvxtDQEN5//33s27cPLpeLr+PxeDA1NYVMJoNwOAxN0zAwMMAEmM/n8eSTT+LUqVO8hfmRRx7hH5XNZsOnn36KNWvWoKWlBQ899BAikQiCwSAnxyeZKBAIQJZlJBIJ+Hw+AEA4HMb69evR39+P0dFR2O121ugzmQzeffdd7Nixg/N4VCoVJJNJ/pw09kKhgL1793IC/lgsho6ODpRKJQSDQWSzWcTjcbhcLoTDYV7BDA8PsyRloHFQz4LWk3I98q137HxkXA/1yH0mJ6K+PbOx4ut9vtCa+WwwJws5FApp9913HxwOB5NeOp2G1+sFAC5J1NXVheHhYciyzHouWbzj4+OsXQKoqaBBURxNTU2IRqPw+/2sPZMlHQqF8OOPPyKfz9fo0B6Ph/XctrY2rtZBEwYtu0ulEiYmJtDa2oply5ZheHgYV1xxBc6dO8ebIJYuXYqzZ8/yg/f5fIhEIjXOQa/Xi8nJSdhsNpw8eRIPPPAAli1bhq+//prDv8bHx7FlyxYcO3YM//nPf2AymXDixAlOSHTixAn09fVxpW4KJyTnl6IoWLlyJZqbmzEyMoJ8Po/Dhw/D5/NhaGgIQ0ND0DQNe/fuhdlshqIoSCQSbJlarVZ0dXVhaGgIbW1tHI8syzKGhoZ4k0epVILH44HdbucICqqGMjIyguuvv5515vHxcYTDYUxMTCCXy+Haa6/FwMAAZFkGADidTiSTSdjtdiiKwmOhqiqPF13LbrdjamoKgUAAqqrizTffRCQS+c1ZyL8mXVbPF7NxgtXDTJbzQmrjF2p7vRXBpcKCOPWCwaDW19fHJEgOPNIpyUvvdrtZHySQJksOK9KFAbBuSc4nWZbhdDq5coUmhKeRdez1ehGLxWC325HNZnmjREtLCzsYM5kMTCYTOjs78fPPP8NisSAUCjFRWK1WjrsV8z1QEVeg6kSk+GNy/JHTqlgswu/3o1gsIp1Ow+FwsKZuMpmQy+XQ1tbGk5fb7cbw8DCampqQSCSYlAKBAMcnW61WLu1ksVgwOjqKUCjEkRKRSIQtZ4pRVlUVDocDQHXDDMV1m0wmOBwOjnixWq3IZDK8k5FirikxEU04TqeTo1NsNhtvRLHb7Th37hx6enqQTCaxcuVK5PN5Dtez2+04dOgQVq9ejTNnzkBRlBorPpPJsKSUzWbh8XiQyWQQDAYRjUZx8OBBnDt37jdHyP+fMBOfzIW4L0fUxfnuez4JZQ73uPSEHAqFtJ07d3LMsaZp6O7uRiQSQXNzM1paWhCLxdgRpSgKbwghKUO8n0iKlJyHyIY88xR2ViwWOYaZwqsoNE3Tqjv4Ojo60N/fD5vNhnK5DK/XC0VROCqjUqmwIyyVSsHlcjGxWa1W1sQ1rVr1w2q1QpZlTE1Nob29nYm3Xq5mmpTEFKPktKSJgTZESJKEYDAIk8mEaDSKSqXCuwnJsUbhdx6Pp2YCWr58OaampjA2NgaPx1MTQRGNRuHz+ZDP55HJZOB0OjmygaJPcrkcgsEgUqkU3w+oRj6Q7muxWBCPxzlnR7lchsPh4NhksrSBqq4syzJcLheampqwfPlyqKqKbDbLk6oYyXL69GlEIhGODKFdk6qq4v333/9NWsgGGhuXwlpeEEKWJCkGYGi+jTJg4ALo1jTNv9g3NX7XBhYYs/5dz4mQDRgwYMDAwmHOuSwMGDBgwMDCwCBkAwYMGGgQGIRswIABAw0Cg5ANGDBgoEFgELIBAwYMNAgMQjZgwICBBoFByAYMGDDQIDAI2YABAwYaBAYhGzBgwECD4P8A7N2VUG9IU+UAAAAASUVORK5CYII=" alt="" width="448" height="161" />
官方结果

更多资源
1. Canny edge detector at Wikipedia
2. Canny Edge Detection Tutorial by Bill Green, 2002.
练习
1. 写一个小程序,可以通过调节滑动条来设置阈值 minVal 和 maxVal 进而来进行 Canny 边界检测。这样你就会理解阈值的重要性了。
20 图像金字塔
目标
• 学习图像金字塔
• 使用图像创建一个新水果:“橘子苹果”
• 将要学习的函数有:cv2.pyrUp(),cv2.pyrDown()。
20.1 原理
一般情况下,我们要处理是一副具有固定分辨率的图像。但是有些情况下,我们需要对同一图像的不同分辨率的子图像进行处理。比如,我们要在一幅图像中查找某个目标,比如脸,我们不知道目标在图像中的尺寸大小。这种情况下,我们需要创建创建一组图像,这些图像是具有不同分辨率的原始图像。我们把这组图像叫做图像金字塔(简单来说就是同一图像的不同分辨率的子图集合)。如果我们把最大的图像放在底部,最小的放在顶部,看起来像一座金字塔,故而得名图像金字塔。
有两类图像金字塔:高斯金字塔和拉普拉斯金字塔。
高斯金字塔的顶部是通过将底部图像中的连续的行和列去除得到的。顶部图像中的每个像素值等于下一层图像中 5 个像素的高斯加权平均值。这样操作一次一个 MxN 的图像就变成了一个 M/2xN/2 的图像。所以这幅图像的面积就变为原来图像面积的四分之一。这被称为 Octave。连续进行这样的操作我们就会得到一个分辨率不断下降的图像金字塔。我们可以使用函数cv2.pyrDown() 和 cv2.pyrUp() 构建图像金字塔。
函数 cv2.pyrDown() 从一个高分辨率大尺寸的图像向上构建一个金子塔(尺寸变小,分辨率降低)。
img = cv2.imread('messi5.jpg')
lower_reso = cv2.pyrDown(higher_reso)
下图是一个四层的图像金字塔。

函数 cv2.pyrUp() 从一个低分辨率小尺寸的图像向下构建一个金子塔(尺寸变大,但分辨率不会增加)。
higher_reso2 = cv2.pyrUp(lower_reso)

你要记住的是是 higher_reso2 和 higher_reso 是不同的。因为一旦使用 cv2.pyrDown(),图像的分辨率就会降低,信息就会被丢失。下图就是从 cv2.pyrDown() 产生的图像金字塔的(由下到上)第三层图像使用函数cv2.pyrUp() 得到的图像,与原图像相比分辨率差了很多。
拉普拉斯金字塔可以有高斯金字塔计算得来,公式如下:
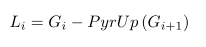
拉普拉金字塔的图像看起来就像边界图,其中很多像素都是 0。他们经常被用在图像压缩中。下图就是一个三层的拉普拉斯金字塔:

20.2 使用金字塔进行图像融合
图像金字塔的一个应用是图像融合。例如,在图像缝合中,你需要将两幅图叠在一起,但是由于连接区域图像像素的不连续性,整幅图的效果看起来会很差。这时图像金字塔就可以排上用场了,他可以帮你实现无缝连接。这里的一个经典案例就是将两个水果融合成一个,看看下图也许你就明白我在讲什么了。

你可以通过阅读后边的更多资源来了解更多关于图像融合,拉普拉斯金字塔的细节。
实现上述效果的步骤如下:
1. 读入两幅图像,苹果和句子
2. 构建苹果和橘子的高斯金字塔(6 层)
3. 根据高斯金字塔计算拉普拉斯金字塔
4. 在拉普拉斯的每一层进行图像融合(苹果的左边与橘子的右边融合)
5. 根据融合后的图像金字塔重建原始图像。
下图是摘自《学习 OpenCV》展示了金子塔的构建,以及如何从金字塔重建原始图像的过程。
整个过程的代码如下。(为了简单,每一步都是独立完成的,这回消耗更多、的内存,如果你愿意的话可以对他进行优化)
import cv2
import numpy as np,sys A = cv2.imread('apple.jpg')
B = cv2.imread('orange.jpg') # generate Gaussian pyramid for A
G = A.copy()
gpA = [G]
for i in xrange(6):
G = cv2.pyrDown(G)
gpA.append(G) # generate Gaussian pyramid for B
G = B.copy()
gpB = [G]
for i in xrange(6):
G = cv2.pyrDown(G)
gpB.append(G) # generate Laplacian Pyramid for A
lpA = [gpA[5]]
for i in xrange(5,0,-1):
GE = cv2.pyrUp(gpA[i])
L = cv2.subtract(gpA[i-1],GE)
lpA.append(L) # generate Laplacian Pyramid for B
lpB = [gpB[5]]
for i in xrange(5,0,-1):
GE = cv2.pyrUp(gpB[i])
L = cv2.subtract(gpB[i-1],GE)
lpB.append(L) # Now add left and right halves of images in each level
LS = []
for la,lb in zip(lpA,lpB):
rows,cols,dpt = la.shape
ls = np.hstack((la[:,0:cols/2], lb[:,cols/2:]))
LS.append(ls) # now reconstruct
ls_ = LS[0]
for i in xrange(1,6):
ls_ = cv2.pyrUp(ls_)
ls_ = cv2.add(ls_, LS[i]) # image with direct connecting each half
real = np.hstack((A[:,:cols/2],B[:,cols/2:])) cv2.imwrite('Pyramid_blending2.jpg',ls_)
cv2.imwrite('Direct_blending.jpg',real)
[OpenCV-Python] OpenCV 中的图像处理 部分 IV (三)的更多相关文章
- [OpenCV-Python] OpenCV 中的图像处理 部分 IV (一)
部分 IVOpenCV 中的图像处理 OpenCV-Python 中文教程(搬运)目录 13 颜色空间转换 目标 • 你将学习如何对图像进行颜色空间转换,比如从 BGR 到灰度图,或者从BGR 到 ...
- [OpenCV-Python] OpenCV 中的图像处理 部分 IV (四)
部分 IVOpenCV 中的图像处理 OpenCV-Python 中文教程(搬运)目录 21 OpenCV 中的轮廓 21.1 初识轮廓目标 • 理解什么是轮廓 • 学习找轮廓,绘制轮廓等 • 函数: ...
- [OpenCV-Python] OpenCV 中的图像处理 部分 IV (五)
部分 IVOpenCV 中的图像处理 OpenCV-Python 中文教程(搬运)目录 22 直方图 22.1 直方图的计算,绘制与分析目标 • 使用 OpenCV 或 Numpy 函数计算直方图 • ...
- [OpenCV-Python] OpenCV 中的图像处理 部分 IV (六)
部分 IVOpenCV 中的图像处理 OpenCV-Python 中文教程(搬运)目录 23 图像变换 23.1 傅里叶变换目标本小节我们将要学习: • 使用 OpenCV 对图像进行傅里叶变换 • ...
- [OpenCV-Python] OpenCV 中的图像处理 部分 IV (二)
部分 IVOpenCV 中的图像处理 OpenCV-Python 中文教程(搬运)目录 16 图像平滑 目标 • 学习使用不同的低通滤波器对图像进行模糊 • 使用自定义的滤波器对图像进行卷积(2D 卷 ...
- .NET + OpenCV & Python + OpenCV 配置
最近需要做一个图像识别的GUI应用,权衡了Opencv+ 1)QT,2)Python GUI,3).NET后选择了.NET... 本文给出C#+Opencv和Python+Opencv的相应参考,节省 ...
- Python虚拟机中的一般表达式(三)
其他一般表达式 在前两章:Python虚拟机中的一般表达式(一).Python虚拟机中的一般表达式(二)中,我们介绍了Python虚拟机是怎样执行创建一个整数值对象.字符串对象.字典对象和列表对象.现 ...
- Python post中session和auth 的三种方法
1.方式一,获取session后.存储起来.下次调用时候,传递一个session植即可 #/bin/python # -*- coding: utf-8 -*- import requests fro ...
- opencv python实用操作
画多边形 fillConvexPloy与fillConvexPloy的区别 fillConvexPloy 用来画单个凸多边形: 如果点集的连线不是凹多边形,则会找一个最小的凸多边形把该凹多边形包住画出 ...
随机推荐
- Git查看单个文件修改历史
1 命令 git log --pretty=oneline 文件名 ➜ admin git:(feature/v1.5.0_20181202_group) git log --pretty=onel ...
- vue学习之用 Vue.js + Vue Router 创建单页应用的几个步骤
通过vue学习一:新建或打开vue项目,创建好项目后,接下来的操作为: src目录重新规划——>新建几个页面——>配置这几个页面的路由——>给根实例注入路由配置 src目录重整 在项 ...
- C - Little Jumper (三分)
题目链接:https://cn.vjudge.net/contest/281961#problem/C 题目大意:青蛙能从一个点跳到第三个点,如图,需要跳两次.问整个过程的最大起跳速度中的最小的. 具 ...
- Python提示AttributeError 或者DeprecationWarning: This module was deprecated解决方法
Python提示AttributeError 或者DeprecationWarning: This module was deprecated解决方法 在使用Python的sklearn库时,发现sk ...
- python内置模块之collections(六)
前言 collections是Python内建的一个集合模块,提供了许多有用的集合类. 系列文章 python模块分析之random(一) python模块分析之hashlib加密(二) python ...
- 在12C上创建wm_concat函数
11gr2和12C上已经摒弃了wm_concat函数,当时我们很多程序员在程序中确使用了该函数,导致程序出现错误,为了减轻程序员修改程序的工作量,只有通过手工创建个wm_concat函数,来临时解决该 ...
- java中不同类型的数值占用字节数
在Java中一共有8种基本数据类型,其中有4种整型,2种浮点类型,1种用于表示Unicode编码的字符单元的字符类型和1种用于表示真值的boolean类型.(一个字节等于8个bit) 1.整型 类型 ...
- mysql安装与卸载(非绿色版)
一.安装和卸载 Mysql安装路径: C:\Program Files\MySQL\MySQL Server 5.5\ Mysql数据文件存放的路径: C:\Documents and Setting ...
- C# 多种方式连接Oracle。
废话不多说直接正题: 首先我们先在Oracle数据库下建了一个用户叫做lisi,密码为lisi,在这个用户下建立一张表叫做“USERS”,在这个表下新增三个数据. 方式一:利用OleDb连接Oracl ...
- Jquery hover方法使用及 mouseenter与mouseleave和 mouseover与mouseout的区别
定义和用法 hover() 方法规定当鼠标指针悬停在被选元素上时要运行的两个函数. jQuery 1.7 版本前该方法触发 mouseenter 和 mouseleave 事件. jQuery 1.8 ...
