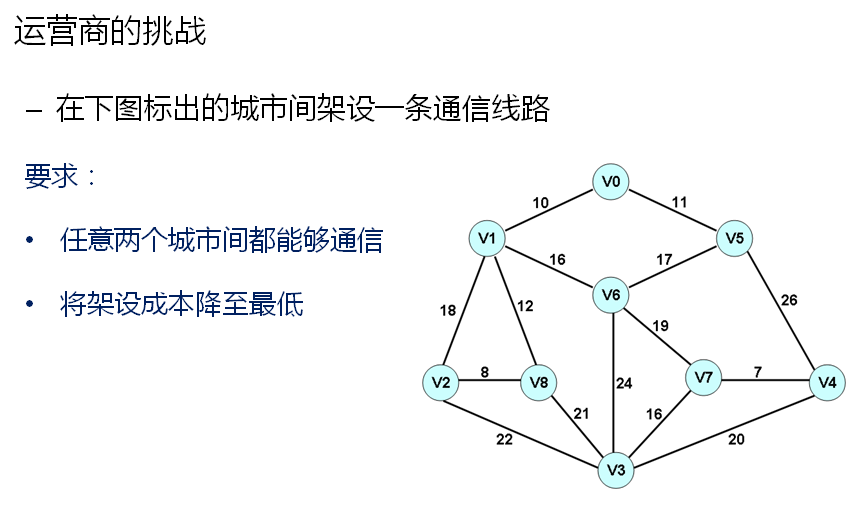
第76课 最小生成树(Prim)


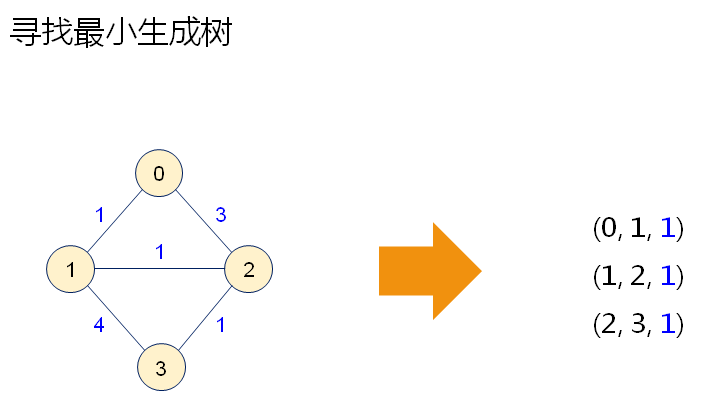
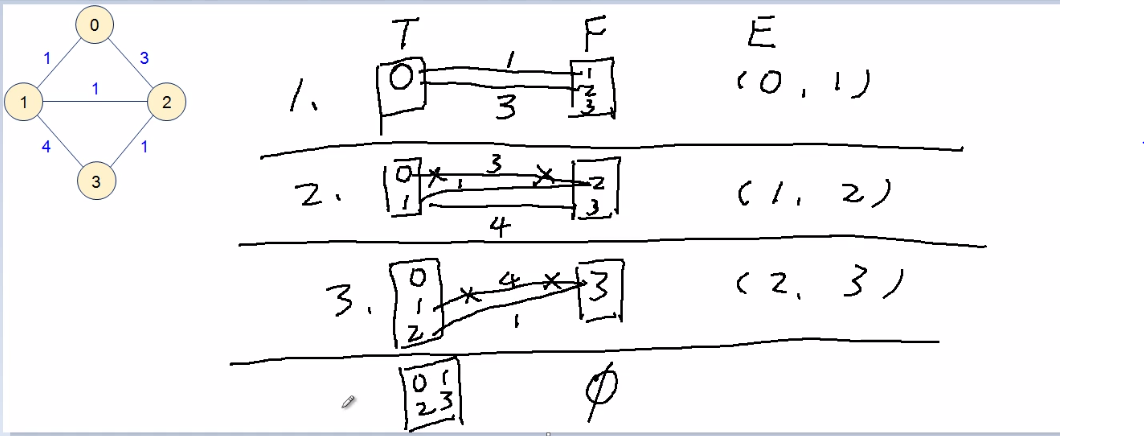
图解:

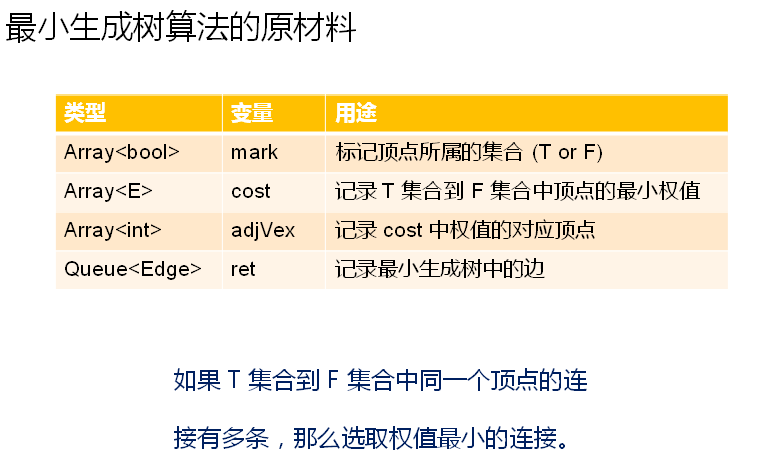




添加prim函数:
#ifndef GRAPH_H
#define GRAPH_H #include "Object.h"
#include "SharedPointer.h"
#include "Array.h"
#include "DynamicArray.h"
#include "LinkQueue.h"
#include "LinkStack.h" namespace DTLib
{ template < typename E >
struct Edge : public Object
{
int b;
int e;
E data; Edge(int i=-, int j=-)
{
b = i;
e = j;
} Edge(int i, int j, const E& value)
{
b = i;
e = j;
data = value;
} bool operator == (const Edge<E>& obj)
{
return (b == obj.b) && (e == obj.e); //在这里不关注权值大小
} bool operator != (const Edge<E>& obj)
{
return !(*this == obj);
}
}; template < typename V, typename E >
class Graph : public Object
{
protected:
template < typename T >
DynamicArray<T>* toArray(LinkQueue<T>& queue)
{
DynamicArray<T>* ret = new DynamicArray<T>(queue.length()); if( ret != NULL )
{
for(int i=; i<ret->length(); i++, queue.remove())
{
ret->set(i, queue.front());
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object...");
} return ret;
}
public:
virtual V getVertex(int i) = ;
virtual bool getVertex(int i, V& value) = ;
virtual bool setVertex(int i, const V& value) = ;
virtual SharedPointer< Array<int> > getAdjacent(int i) = ;
virtual bool isAdjacent(int i, int j) = ;
virtual E getEdge(int i, int j) = ;
virtual bool getEdge(int i, int j, E& value) = ;
virtual bool setEdge(int i, int j, const E& value) = ;
virtual bool removeEdge(int i, int j) = ;
virtual int vCount() = ;
virtual int eCount() = ;
virtual int OD(int i) = ;
virtual int ID(int i) = ; virtual int TD(int i)
{
return ID(i) + OD(i);
} bool asUndirected()
{
bool ret = true; for(int i=; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
if( isAdjacent(i, j) )
{
ret = ret && isAdjacent(j, i) && (getEdge(i, j) == getEdge(j, i));
}
}
} return ret;
} SharedPointer< Array< Edge<E > > > prim(const E& LIMIT) //参数为理论上的最大权值
{
LinkQueue< Edge<E> > ret; if( asUndirected() )
{
DynamicArray<int> adjVex(vCount());
DynamicArray<bool> mark(vCount());
DynamicArray<E> cost(vCount());
SharedPointer< Array<int> > aj = NULL;
bool end = false;
int v = ; for(int i=; i<vCount(); i++)
{
adjVex[i] = -;
mark[i] = false;
cost[i] = LIMIT;
} mark[v] = true; aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
cost[(*aj)[j]] = getEdge(v, (*aj)[j]);
adjVex[(*aj)[j]] = v;
} for(int i=; (i<vCount()) && !end; i++)
{
E m = LIMIT;
int k = -; for(int j=; j<vCount(); j++)
{
if( !mark[j] && (cost[j] < m))
{
m = cost[j];
k = j;
}
} end = (k == -); if( !end )
{
ret.add(Edge<E>(adjVex[k], k, getEdge(adjVex[k], k))); mark[k] = true; aj = getAdjacent(k); for(int j=; j<aj->length(); j++)
{
if( !mark[(*aj)[j]] && (getEdge(k, (*aj)[j]) < cost[(*aj)[j]]) )
{
cost[(*aj)[j]] = getEdge(k, (*aj)[j]);
adjVex[(*aj)[j]] = k;
}
}
}
}
}
else
{
THROW_EXCEPTION(InvalidOperationException, "Prim operator is for undirected graph only...");
} if( ret.length() != (vCount() - ) )
{
THROW_EXCEPTION(InvalidOperationException, "No enough edge for prim operation...");
} return toArray(ret);
} SharedPointer< Array<int> > BFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkQueue<int> q;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int i=; i<visited.length(); i++)
{
visited[i] = false;
} q.add(i); while( q.length() > )
{
int v = q.front(); q.remove(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
q.add((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} SharedPointer< Array<int> > DFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkStack<int> s;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int j=; j<visited.length(); j++)
{
visited[j] = false;
} s.push(i); while( s.size() > )
{
int v = s.top(); s.pop(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=aj->length() - ; j>=; j--)
{
s.push((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} }; } #endif // GRAPH_H
测试程序如下:
#include <iostream>
#include "MatrixGraph.h"
#include "ListGraph.h" using namespace std;
using namespace DTLib; template< typename V, typename E >
Graph<V, E>& GraphEasy()
{
static MatrixGraph<, V, E> g; g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); return g;
} template< typename V, typename E >
Graph<V, E>& GraphComplex()
{
static ListGraph<V, E> g(); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); return g;
} int main()
{
Graph<int, int>& g = GraphEasy<int, int>(); SharedPointer< Array< Edge<int> > > sa = g.prim(); int w = ; for(int i=; i<sa->length(); i++)
{
w += (*sa)[i].data;
cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl;
} cout << "Weight: " << w << endl; return ;
}
结果如下:

复杂图的结果如下:
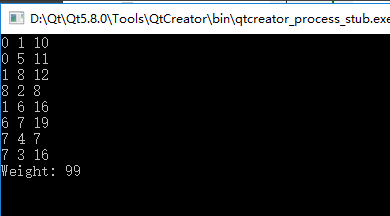
改进函数,支持最大生成树:
#ifndef GRAPH_H
#define GRAPH_H #include "Object.h"
#include "SharedPointer.h"
#include "Array.h"
#include "DynamicArray.h"
#include "LinkQueue.h"
#include "LinkStack.h" namespace DTLib
{ template < typename E >
struct Edge : public Object
{
int b;
int e;
E data; Edge(int i=-, int j=-)
{
b = i;
e = j;
} Edge(int i, int j, const E& value)
{
b = i;
e = j;
data = value;
} bool operator == (const Edge<E>& obj)
{
return (b == obj.b) && (e == obj.e); //在这里不关注权值大小
} bool operator != (const Edge<E>& obj)
{
return !(*this == obj);
}
}; template < typename V, typename E >
class Graph : public Object
{
protected:
template < typename T >
DynamicArray<T>* toArray(LinkQueue<T>& queue)
{
DynamicArray<T>* ret = new DynamicArray<T>(queue.length()); if( ret != NULL )
{
for(int i=; i<ret->length(); i++, queue.remove())
{
ret->set(i, queue.front());
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create ret object...");
} return ret;
}
public:
virtual V getVertex(int i) = ;
virtual bool getVertex(int i, V& value) = ;
virtual bool setVertex(int i, const V& value) = ;
virtual SharedPointer< Array<int> > getAdjacent(int i) = ;
virtual bool isAdjacent(int i, int j) = ;
virtual E getEdge(int i, int j) = ;
virtual bool getEdge(int i, int j, E& value) = ;
virtual bool setEdge(int i, int j, const E& value) = ;
virtual bool removeEdge(int i, int j) = ;
virtual int vCount() = ;
virtual int eCount() = ;
virtual int OD(int i) = ;
virtual int ID(int i) = ; virtual int TD(int i)
{
return ID(i) + OD(i);
} bool asUndirected()
{
bool ret = true; for(int i=; i<vCount(); i++)
{
for(int j=; j<vCount(); j++)
{
if( isAdjacent(i, j) )
{
ret = ret && isAdjacent(j, i) && (getEdge(i, j) == getEdge(j, i));
}
}
} return ret;
} SharedPointer< Array< Edge<E > > > prim(const E& LIMIT, const bool MINIUM = true) //参数为理论上的最大权值
{
LinkQueue< Edge<E> > ret; if( asUndirected() )
{
DynamicArray<int> adjVex(vCount());
DynamicArray<bool> mark(vCount());
DynamicArray<E> cost(vCount());
SharedPointer< Array<int> > aj = NULL;
bool end = false;
int v = ; for(int i=; i<vCount(); i++)
{
adjVex[i] = -;
mark[i] = false;
cost[i] = LIMIT;
} mark[v] = true; aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
cost[(*aj)[j]] = getEdge(v, (*aj)[j]);
adjVex[(*aj)[j]] = v;
} for(int i=; (i<vCount()) && !end; i++)
{
E m = LIMIT;
int k = -; for(int j=; j<vCount(); j++)
{
if( !mark[j] && (MINIUM ? (cost[j] < m) : (cost[j] > m)))
{
m = cost[j];
k = j;
}
} end = (k == -); if( !end )
{
ret.add(Edge<E>(adjVex[k], k, getEdge(adjVex[k], k))); mark[k] = true; aj = getAdjacent(k); for(int j=; j<aj->length(); j++)
{
if( !mark[(*aj)[j]] && (MINIUM ? (getEdge(k, (*aj)[j]) < cost[(*aj)[j]]) : (getEdge(k, (*aj)[j]) > cost[(*aj)[j]])) )
{
cost[(*aj)[j]] = getEdge(k, (*aj)[j]);
adjVex[(*aj)[j]] = k;
}
}
}
}
}
else
{
THROW_EXCEPTION(InvalidOperationException, "Prim operator is for undirected graph only...");
} if( ret.length() != (vCount() - ) )
{
THROW_EXCEPTION(InvalidOperationException, "No enough edge for prim operation...");
} return toArray(ret);
} SharedPointer< Array<int> > BFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkQueue<int> q;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int i=; i<visited.length(); i++)
{
visited[i] = false;
} q.add(i); while( q.length() > )
{
int v = q.front(); q.remove(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=; j<aj->length(); j++)
{
q.add((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} SharedPointer< Array<int> > DFS(int i)
{
DynamicArray<int>* ret = NULL; if( ( <= i) && (i < vCount()) )
{
LinkStack<int> s;
LinkQueue<int> r;
DynamicArray<bool> visited(vCount()); for(int j=; j<visited.length(); j++)
{
visited[j] = false;
} s.push(i); while( s.size() > )
{
int v = s.top(); s.pop(); if( !visited[v] )
{
SharedPointer< Array<int> > aj = getAdjacent(v); for(int j=aj->length() - ; j>=; j--)
{
s.push((*aj)[j]);
} r.add(v); visited[v] = true;
}
} ret = toArray(r);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Index i is invalid...");
} return ret;
} }; } #endif // GRAPH_H
测试程序如下:
#include <iostream>
#include "MatrixGraph.h"
#include "ListGraph.h" using namespace std;
using namespace DTLib; template< typename V, typename E >
Graph<V, E>& GraphEasy()
{
static MatrixGraph<, V, E> g; g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); return g;
} template< typename V, typename E >
Graph<V, E>& GraphComplex()
{
static ListGraph<V, E> g(); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); g.setEdge(, , );
g.setEdge(, , ); return g;
} int main()
{
Graph<int, int>& g = GraphComplex<int, int>(); SharedPointer< Array< Edge<int> > > sa = g.prim(, false); int w = ; for(int i=; i<sa->length(); i++)
{
w += (*sa)[i].data;
cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl;
} cout << "Weight: " << w << endl; return ;
}
结果如下:
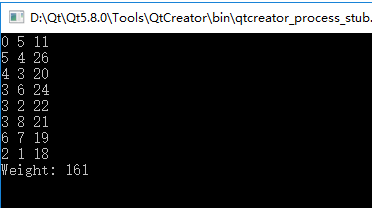
小结:

第76课 最小生成树(Prim)的更多相关文章
- 数据结构代码整理(线性表,栈,队列,串,二叉树,图的建立和遍历stl,最小生成树prim算法)。。持续更新中。。。
//归并排序递归方法实现 #include <iostream> #include <cstdio> using namespace std; #define maxn 100 ...
- 邻接矩阵c源码(构造邻接矩阵,深度优先遍历,广度优先遍历,最小生成树prim,kruskal算法)
matrix.c #include <stdio.h> #include <stdlib.h> #include <stdbool.h> #include < ...
- 最小生成树Prim算法(邻接矩阵和邻接表)
最小生成树,普利姆算法. 简述算法: 先初始化一棵只有一个顶点的树,以这一顶点开始,找到它的最小权值,将这条边上的令一个顶点添加到树中 再从这棵树中的所有顶点中找到一个最小权值(而且权值的另一顶点不属 ...
- 转载:最小生成树-Prim算法和Kruskal算法
本文摘自:http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html 最小生成树-Prim算法和Kruskal算法 Prim算 ...
- 最小生成树Prim
首先解释什么是最小生成树,最小生成树是指在一张图中找出一棵树,任意两点的距离已经是最短的了. 算法要点: 1.用book数组存放访问过的节点. 2.用dis数组保存对应下标的点到树的最近距离,这里要注 ...
- 最小生成树—prim算法
最小生成树prim算法实现 所谓生成树,就是n个点之间连成n-1条边的图形.而最小生成树,就是权值(两点间直线的值)之和的最小值. 首先,要用二维数组记录点和权值.如上图所示无向图: int map[ ...
- 最小生成树Prim算法和Kruskal算法
Prim算法(使用visited数组实现) Prim算法求最小生成树的时候和边数无关,和顶点树有关,所以适合求解稠密网的最小生成树. Prim算法的步骤包括: 1. 将一个图分为两部分,一部分归为点集 ...
- 最小生成树 Prim Kruskal
layout: post title: 最小生成树 Prim Kruskal date: 2017-04-29 tag: 数据结构和算法 --- 目录 TOC {:toc} 最小生成树Minimum ...
- POJ1258 (最小生成树prim)
Agri-Net Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 46319 Accepted: 19052 Descri ...
随机推荐
- TP5+jquery即点既改
//表单 {volist name="date" id="v"}<tr id="{$v.id}"> <td>< ...
- CURD插件(仿Django-admin版)
前言 如何提升自己的开发效率? 每个新项目都是自己经做过的项目(经验所致),在项目开发过程中不断总结.封装属于自己的组件, 例如:每个web项目大部分都涉及增删改查,分页显示,搜素,CRM就是这样的组 ...
- RCNN 目标识别基本原理
RCNN- 将CNN引入目标检测的开山之作 from:https://zhuanlan.zhihu.com/p/23006190 前面一直在写传统机器学习.从本篇开始写一写 深度学习的内容. 可能需要 ...
- redis sentinel哨兵模式集群搭建教程
1.环境说明 我们将使用192.168.220.128.192.168.220.129两台机器搭建sentinel交叉主从为例 当前我们已在192.168.220.128上按redis安装教程安装了r ...
- 逆袭之旅DAY16.东软实训.Oracle.序列
2018-07-12 14:07:44 序列 序列1.创建序列create sequence 序列名 [increment by n] ---步长 [start with n] ---序列的起始值 序 ...
- 模块化&os&sys
syspath python 使用import模块调用的优先级是根据sys.path路径来的,此变量中位置在列表中的先后顺序来调用,如果先找到对应的模块,则先调用此模块. import sys pri ...
- java⑩
1.for循环: for循环语法 for(表达式1;表达式2;表达式3){ 循环体4} 表达式1:初始化变量 只执行一次!表达式2:循环条件 满足条件进入循环体4表达式3:迭代变量 如果循环体 中只有 ...
- 重写equals() 和 hashCode()方法
什么情况下需要重写呢? 比如去重操作时, 有时候往Set集合存放对象User,我们User类的字段太多时,比如有50个字段, 判断两个User对象相同,不需要判断它们所有字段都相同,只需要判断它们的某 ...
- 第三篇 功能实现(2) (Android学习笔记)
第三篇 功能实现(2) ●Activity的四种启动模式 Activity的启动模式有四种,分别是standard.singleTop.singleTask和singleInstance. 在Andr ...
- PSP0级记录2
上课 编写程序 课外资料 日总计 3.13 周一 ...
