PCA原理解释（二）

PCA在做数据处理，一般会有一个数据预处理，其中一个目标就是将取数据特征向相关性。

为什么要去特征的相关性？

因为数据如果有相关性，在学习的时候是冗余的，徒增学习成本；所以对于数据处理（也称之为白化，英文有的时候称之为sphering），白化的目的：1.实现特征之间的相关性较低；2.所有的特征具有相同的方差。

怎么去特征相关性，就是让他们的协方差为0，协方差，顾名思义，就是两组变量的协同性，如果两个变量的变化趋势是一致的，某个变量范围内，取值同样趋于增大、减少，这个时候，协方差就是正常，如果变化趋势相反，协方差就是正直；那么如果两个变量（函数）的变化趋势无关，协方差取值是0.

如果：E(X)=m，E（Y）=v，协方差公式如下：

cov(X,Y) = E((X-m)(Y-v)) = E(X*Y) - mv

如果E(X)和E(Y)两者独立，则协方差为0，这是因为：

E(X*Y) = E(X)E(Y) = mv

这里在深入讲一下，什么是期望？在学习概率的时候，前面几章都是在讲述分布（正态分布，0,1分布，T分布），分布讲述的数据的规律，期望讲述的一个值，用一个数来代表你的这些数集，这个就是期望，也称之为均值，我们看一下期望的公式：

 

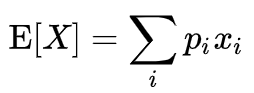
你就会发现其实无论是离散的概率还是连续的期望都是计算求全平均，这就印证上面说的：找一个数来代表你的这个分布；在numpy的array里面有一个mean函数，就是计算期望的。

讲到期望，就要说一下中心化（centered），所谓中心化就是列之间的期望为0。或者说PCA认为各个点都是以原点为中心来进行分散的。

 

SVD：奇异值分解，Singular Value Decomposition.

他的思路就是将一个矩阵（无论多复杂）用三个矩阵相乘得来：

其中M就是原始矩阵，U是M.dot(M.T)的特征向量，V是M.T.dot(M)的向量，Sigma就是一个对角矩阵。里面的元素就是奇异值。

关于矩阵乘法和特征值

矩阵的乘法（dot）本质其实是将一个矩阵中的向量从长度（伸缩）到方向（旋转）进行转变；如果一个M.dot(N)，只是有伸缩但是没有旋转，那么这个N就是M的特征向量。

那么回归本源，什么是特征值，特征向量？

对于矩阵A，如果存在数m以及向量x，满足Ax=mx，则成m为A的特征值，x是矩阵A对于m特征值的特征向量。

PCA中的核函数

很多时候，降维是为了减少数据量，提高运算速度；但是有的时候低维度的数据不好对数据进行划分，这个时候需要将数据提高维度，很多时候，高纬度数据反而更好找到super plane来对数据进行划分，那么核函数就是做这件事情的，通过提高维度来进行数据划分，将底维数据向高维数据做映射的函数，就是"核函数（kernel function）"。在sklearn里面就有KernelPCA用于为PCA指定核函数。

提到了PCA一定要提一下无偏估计。因为PCA的有一部分就是就协方差的。

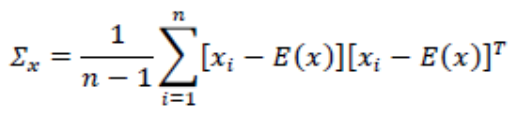
方差嘛，本来应该是[X-E(X)]**2，但是主要，你现在出列都是矩阵，所以如果想要实现平方，是需要和他的转置矩阵相乘来处理的。

 

 

参考：

关于SVD很硬的一篇博客

https://www.cnblogs.com/lzllovesyl/p/5243370.html