Adaboost\GBDT\GBRT\组合算法

Adaboost\GBDT\GBRT\组合算法（龙心尘老师上课笔记）

一、Bagging （并行bootstrap）& Boosting（串行）

随机森林实际上是bagging的思路，而GBDT和Adaboost实际上是boosting的思路。而bagging和boosting有什么区别呢？怎样从bagging转到boosting呢？

Bagging的假设函数：

如果是二分类问题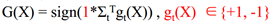：，其中T是分类器的总数，g(x)是其中的小分类器的取值（+1或-1），最后根据各个分类器的值求加和，根据和的符号得到最终大分类器是正还是负。

如果是回归问题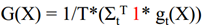：，最后取得是各个小分类器的平均值。

Bagging的特点1.各个学习器相互独立，可以同时并行生成；2.各个学习期权重相同

而Boosting特别大的区别就在于，各个学习器强烈依赖（上一个学习器产生，再产生下一个），串行生成，其中，gbdt（每个学习器权重相同），Adaboost（每个学习器权重不同）。

Boosting要解决的核心问题：

产生不同的训练集（训练集各样本标签不同，训练集各样本抽样权重不同）

产生不同的模型（不同的训练集，就能产生不同模型）

产生不同模型对应的权重

二、GBDT（生成新标签，串行生成树）

假设函数：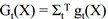

损失函数：均方损失函数

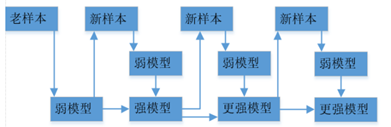
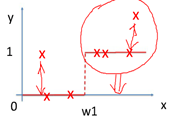
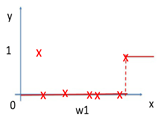
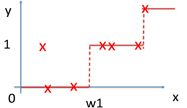
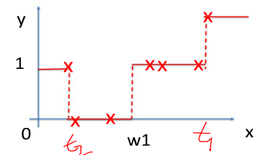
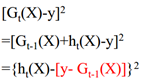其中红色部分是之前集成学习器产生的残差，对应来看，这样可以理解成，红色部分相当于可以把之前学习器的残差，作为原来样本的新标签。这样就产生了新的训练集可以生成新的模型（下面右图2）。集成弱模型，得到强模型（下图3，样本x不变，标签Y变），依次下去重复，直到集合成最强模型。

损失函数：

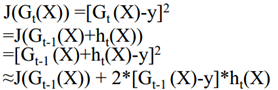（一阶泰勒展开，因为h(x)不是单位长度，所以需要放缩到单位长度，变成有约束条件下的凸优化问题；chargeboost中试二阶展开，就不用放缩了）

从集成学习器变成基学习器，不优化集成学习器整体，而以之前的学习器为已知项（G(X)），优化增加的那个学习器（损失函数也优化基学习器的）。不优化权重整体，而以之前的权重为已知项，优化权重变化的小量。每一步H(X)实际上就是CART树的生成过程。

三、Adaboost（每次新的学习器是基于上一次分类错误的样本，通过关注样本的权重来实现）

可以证明GDBT也是Adaboost的一种，最本质的区别：损失函数不同，指数损失函数：

另一个区别：假设函数不同：

g(x)的取值实际上是+1，-1，然后给一个权重相加，最后只取符号，正的就是+1，负的就是-1；a会越来越小，后面的学习器会越来越弱，所以尽管后面可能有些前面的被分类错误了，影响也不大。一直经历分对，分错，分对，分错的过程，直到损失函数最小，但后面的学习器的分布权重减少。

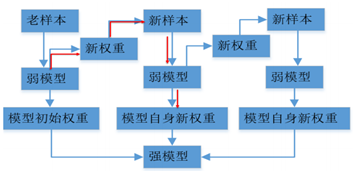
理解Adaboost训练过程

1．  新的弱模型来自于上一个弱模型，而不是之前所有模型的集合（GBDT）

2．  每个弱模型到强模型之前有权重（弱模型自身生成的权重）

3．  新权重，是样本的权重

样本权重：不同的样本分布权重对应不同训练集，类比boostrap，每一次boostrap抽样产生的新的训练集各类别样本比例不一样。（类似于上采样，多复制几遍负样本，也就是给予较多的权重）

基于错误分类的样本，给予权重的放大缩小，以使其分类正确。

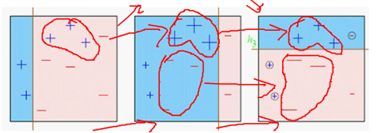
样本的权重（其实是损失函数的系数）：

新的分类器必须是在上一个分类器上表现最差，与上一个分类器不一样，这样才能改进上一个学习器，否者没有什么作用，而二分类问题，表现最差的情况就是拍脑袋分类1/2概率，从而求解权重u_n. 这种方式求解u过麻烦，因而就有了下图中，构造一种递推的方式。

模型的权重：

误差率越小，模型权重越高，也就是说如果一个模型能把所有的都分对，那我们就给予一个很高的权重。

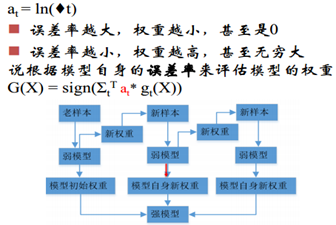
梯度下降理解Adaboost：

要求解的仍然是增加的新学习器的g(x)和模型权重a_t

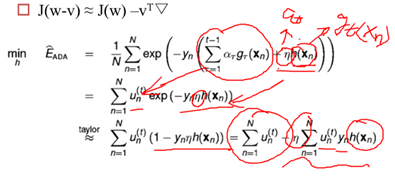
求解h(x)，最优解就是h(x)=gt

求解η，最优解就是模型权重a_t

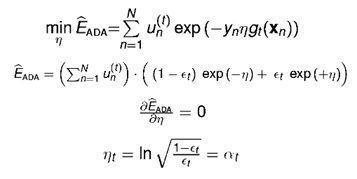
四、集成学习

精英制是加了权重之后再投票。

偏差是算法可能预测出一系列的值，取平均，与真实结果的偏离。方差是训练集数据的变化对学习结果的影响。如果说一个模型偏差高，则是欠拟合；如果说一个模型方差高，则是过拟合。一个模型的误差是由方差、偏差和噪声共同构成。

损失函数，adaboost基学习器的损失还是是0-1损失函数，只是前面加了权重，集成学习器的损失函数为指数损失函数；CART也可以看做集成学习器，看成是每一个树桩的集成学习。