编辑距离12 · Edit Distance12

［抄题］：

给出两个单词word1和word2，计算出将word1 转换为word2的最少操作次数。

你总共三种操作方法：

• 插入一个字符
• 删除一个字符
• 替换一个字符

［思维问题］：

［一句话思路］：

分析双序列变换的所有情况

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

［一刷］：

1. 由于数组多加了一位，所有的上限都要加1
2. Math.min最多一次只能比较2个数

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

注意上限都要加1

［复杂度］：Time complexity: O(n^2) Space complexity: O(n^2)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

双序列型dp

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

583. Delete Operation for Two Strings 只能删除：还是dp

712. Minimum ASCII Delete Sum for Two Strings 加一个ascii转化

[代码风格] ：

else热脸贴冷屁股，不要空格，更不要换行

public class Solution {
    /*
     * @param word1: A string
     * @param word2: A string
     * @return: The minimum number of steps.
     */
    public int minDistance(String word1, String word2) {
        //state
        int m = word1.length();
        int n = word2.length();
        //initialization
        int[][] dp = new int[m + 1][n + 1];
        //m == 0
        for (int i = 0; i < n + 1; i++) {
            dp[0][i] = i;
        }
        // n == 0
        for (int i = 0; i < m + 1; i++) {
            dp[i][0] = i;
        }
        //function
        for (int i = 1; i < m + 1; i++) {
            for (int j = 1; j < n + 1; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                }else {
                    dp[i][j] = 1 + Math.min(dp[i - 1][j - 1],Math.min(dp[i][j - 1],dp[i - 1][j]));
                }
            }
        }
        //answer
        return dp[m][n];
    }
}

一步编辑

［抄题］：

给你两个字符串 S 和 T, 判断他们是否只差一步编辑。

给你字符串 s = "aDb", t= "adb" 
返回 true

[暴力解法]：

时间分析：

空间分析：

［思维问题］：

原始想法：相差一位字母时，每删一个字母，比较字符串是否相同。问题是没有办法比较字符串是否相同。

［一句话思路］：

1. 柿子要找软的捏，从特殊情况讨论开始。
2. 相差一位字母时，删除第一个不相同的字母，用（.substring equals不是==号！）比较剩余的字符串是否相同 下图。

［输入量］：空： 正常情况：特大：特小：程序里处理到的特殊情况：异常情况（不合法不合理的输入）：

［画图］：

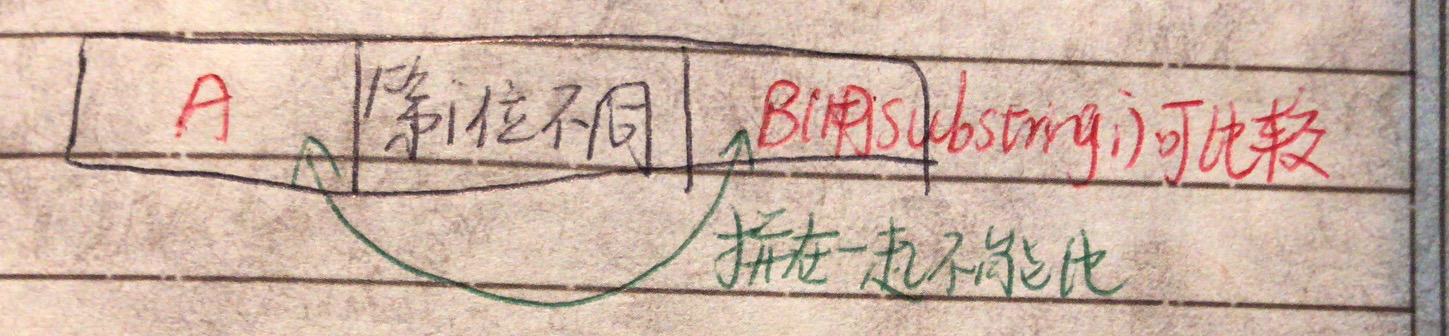
［一刷］：

1. 两个字符串长度不符合，直接在返回函数里取反 isOneEditDistance(t, s)
2. 用count统计不相同的字母个数，为1时才返回true。

［二刷］：

［三刷］：

［四刷］：

［五刷］：

[五分钟肉眼debug的结果]：

［总结］：

注意简写：return true if a = return a

［复杂度］：Time complexity: O(n) Space complexity: O(n)

［英文数据结构或算法，为什么不用别的数据结构或算法］：

由于已经讨论特殊情况了，比较字符串是否相等即可。不用任何的数据结构、算法

［其他解法］：

［Follow Up］：

［LC给出的题目变变变］：

[代码风格] ：