AP聚类算法

一、算法简介

Affinity Propagation聚类算法简称AP，是一个在07年发表在Science上的聚类算法。它实际属于message-passing algorithms的一种。算法的基本思想将数据看成网络中的节点，通过在数据点之间传递消息，分别是吸引度(responsibility)和归属度(availability)，不断修改聚类中心的数量与位置，直到整个数据集相似度达到最大，同时产生高聚类中心，并将其余各点分配到相应的聚类中。

二、算法描述

1、相关概念

• Exemplar：指的是聚类中心，该聚类中心实际存在，并不是如同K-Means算法由计算生成的。

• Similarity：数据点i和点j的相似度记为s(i, j)，是指点j作为点i的聚类中心的相似度。一般使用欧氏距离来计算；相似度值越大说明点与点的距离越近，便于后面的比较计算。

• Preference：数据点i的参考度称为p(i)或s(i,i)，是指点i作为聚类中心的参考度。一般取s相似度值的中值。

• Responsibility：r(i,k)用来描述点k适合作为数据点i的聚类中心的程度。

• Availability：a(i,k)用来描述点i选择点k作为其聚类中心的适合程度。

• Damping factor(阻尼因子)λ：主要是起收敛作用的。

2、算法步骤

2.1 具体算法步骤

AP算法可能需要指定一些参数，如Preference与Damping factor与最大迭代次数maxIte​rNum.

step 1: 初始化参数Damping factor与maxIterNum，并读取数据；

step 2：计算相似度矩阵Similarity[i,j],一般使用欧氏距离，并求出相似度矩阵的中位值并赋给Preference；

step 3: 更新吸引度矩阵；

step 4: 更新归属度矩阵；

setp 4: 判断是否达到最大迭代次数或达到终止条件，如未达到跳转step 2，否则继续下一步；

setp 5: 生成最终Exemplar，并将各数据分配到相应的聚类中。

2.2 算法详解

AP算法有两个关键步骤，即更新吸引度矩阵与更新归属度矩阵。

更新吸引度矩阵：

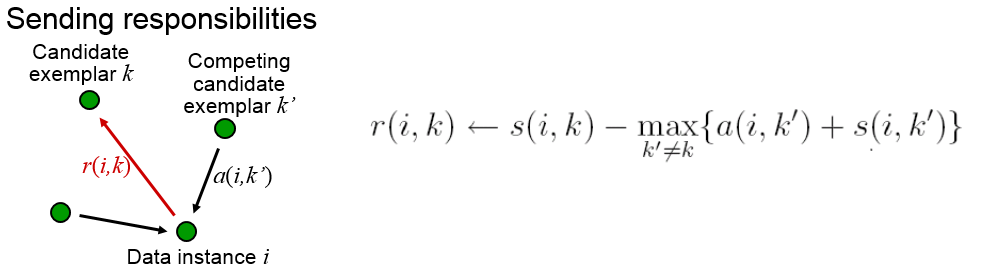
更新归属度矩阵：

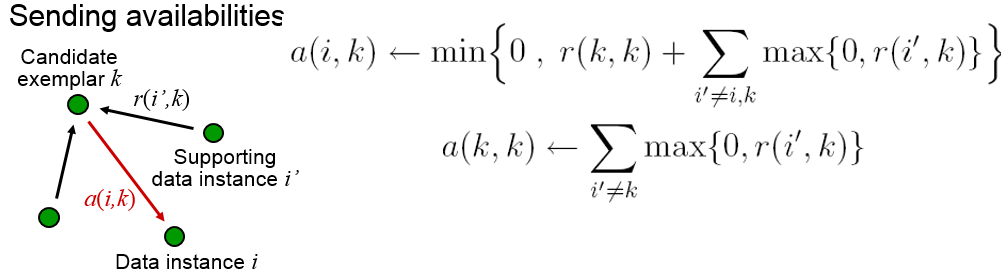
为了避免振荡，AP算法更新信息时引入了衰减系数λ。每条信息被设置为它前次迭代更新值的λ倍加上本次信息更新值的1-λ倍。其中，衰减系数

到1之间的实数。即第t+1次r(i,k)与a(i,k)的迭代值：

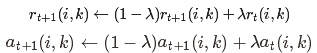
2.3 算法优缺点

优点：

• 不需要事先指定聚类的数量

• 聚类结果很稳定

• 适用于非对称相似性矩阵

• 初始值不敏感

缺点：

• 算法复杂度较高，为O(N*N*logN)，该算法比较慢，对于大量数据，计算很久

三、算法实现（Java）

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380

package cang.algorithms.clustering.ap;   import java.io.BufferedReader; import java.io.FileReader; import java.io.IOException; import java.util.ArrayList; import java.util.Arrays; import java.util.Collections; import java.util.HashMap; import java.util.List; import java.util.Map; import java.util.Map.Entry;   /**  * 近邻传播算法，半监督聚类算法<br>  * 优点：不需事先指定类的个数；对初值的选取不敏感；对距离矩阵的对称性没要求<br>  * 缺点：算法复杂度较高，为O(N*N*logN)  *  * @author cang  *  */ public class AP {       private int maxIterNum;     // 聚类结果不变次数     private int changedCount;     private int unchangeNum;     private int dataNum;     private Point[] dataset;     // 相似度矩阵，数据点i和点j的相似度记为s(i, j)，是指点j作为点i的聚类中心的相似度     private double similar[][];     // 吸引信息矩阵，r(i,k)用来描述点k适合作为数据点i的聚类中心的程度     private double r[][];     // 归属信息矩阵，a(i,k)用来描述点i选择点k作为其聚类中心的适合程度     private double a[][];     // 衰减系数,主要是起收敛作用的     private double lambda;     // 聚类中心     private List<Integer> exemplar;     private List<Integer> oldExemplar;       public AP() {         this(1000, 0.9);     }       public AP(int maxIterNum, double lambda) {         this.maxIterNum = maxIterNum;         this.lambda = lambda;     }       /**      * 数据初始化      */     public void init() {         oldExemplar = new ArrayList<Integer>();         exemplar = new ArrayList<Integer>();         similar = new double[dataNum][dataNum];         r = new double[dataNum][dataNum];         a = new double[dataNum][dataNum];         for (int i = 0; i < dataset.length; i++) {             for (int j = i + 1; j < dataset.length; j++) {                 similar[i][j] = distance(dataset[i].dimensioin,                         dataset[j].dimensioin);                 similar[j][i] = similar[i][j];             }         }         setPreference(3);     }       /**      * 获取数据点i的参考度<br>      * 称为p(i)或s(i,i) 是指点i作为聚类中心的参考度。一般取s相似度值的中值      *      * @param prefType 参考度类型      */     private void setPreference(int prefType) {         List<Double> list = new ArrayList<Double>();         // find the median         for (int i = 0; i < dataNum; i++) {             for (int j = i + 1; j < dataNum; j++) {                 list.add(similar[i][j]);             }         }         Collections.sort(list);         double pref = 0;         // use the median as preference         if (prefType == 1) {             if (list.size() % 2 == 0) {                 pref = (list.get(list.size() / 2)                         + list.get(list.size() / 2 - 1)) / 2;             } else {                 pref = list.get((list.size()) / 2);             }             // use the minimum as preference         } else if (prefType == 2) {             pref = list.get(0);             // use the 0.5 * (min + max) as preference         } else if (prefType == 3) {             pref = list.get(0)                     + (list.get(list.size() - 1) + list.get(0)) * 0.5;             // use the maximum as preference         } else if (prefType == 4) {             pref = list.get(list.size() - 1);         } else {             System.out.println("prefType error");             System.exit(-1);         }         System.out.println(pref);         for (int i = 0; i < dataNum; i++) {             similar[i][i] = pref;         }     }       public void clustering() {         for (int i = 0; i < maxIterNum; i++) {             updateResponsible();             updateAvailable();               oldExemplar.clear();             if (!exemplar.isEmpty()) {                 for (Integer v : exemplar) {                     oldExemplar.add(v);                 }             }             exemplar.clear();               changedCount = 0;             // 获取聚类中心             for (int k = 0; k < dataNum; k++) {                 if (r[k][k] + a[k][k] > 0) {                     exemplar.add(k);                 }             }             // data point assignment             assignCluster();               if (changedCount == 0) {                 unchangeNum++;                 if (unchangeNum > 10) {                     maxIterNum = i;                     break;                 }             } else {                 unchangeNum = 0;             }           }         // 生成预测标签         setPredictLabel();     }       /**      * 将各数据点分配到聚类中心      */     private void assignCluster() {         for (int i = 0; i < dataNum; i++) {             double max = Double.MIN_VALUE;             int index = 0;             for (Integer k : exemplar) {                 if (max < similar[i][k]) {                     max = similar[i][k];                     index = k;                 }             }             if (dataset[i].cid != index) {                 dataset[i].cid = index;                 changedCount++;             }         }     }       /**      * 更新吸引信息矩阵      */     private void updateResponsible() {         for (int i = 0; i < dataNum; i++) {             for (int k = 0; k < dataNum; k++) {                 double max = Double.MIN_VALUE;                 for (int j = 0; j < dataNum; j++) {                     if (j != k) {                         if (max < a[i][j] + similar[i][j]) {                             max = a[i][j] + similar[i][j];                         }                     }                 }                 r[i][k] = (1 - lambda) * (similar[i][k] - max)                         + lambda * r[i][k];             }         }     }       /**      * 更新归属信息矩阵      */     private void updateAvailable() {         for (int i = 0; i < dataNum; i++) {             for (int k = 0; k < dataNum; k++) {                 if (i == k) {                     double sum = 0;                     for (int j = 0; j < dataNum; j++) {                         if (j != k) {                             if (r[j][k] > 0) {                                 sum += r[j][k];                             }                         }                     }                     a[k][k] = sum;                 } else {                     double sum = 0;                     for (int j = 0; j < dataNum; j++) {                         if (j != i && j != k) {                             if (r[j][k] > 0) {                                 sum += r[j][k];                             }                         }                     }                     a[i][k] = (1 - lambda) * (r[k][k] + sum) + lambda * a[i][k];                     if (a[i][k] > 0) {                         a[i][k] = 0;                     }                 }             }         }     }       /**      * 生成数据点的聚类标签      */     private void setPredictLabel() {         Map<Integer, String> labelMap = new HashMap<Integer, String>();         for (int cid : exemplar) {             Map<String, Integer> tempMap = new HashMap<String, Integer>();             for (Point p : dataset) {                 if (cid == p.cid) {                     if (tempMap.get(p.label) == null) {                         tempMap.put(p.label, 1);                     } else {                         tempMap.put(p.label, tempMap.get(p.label) + 1);                     }                 }             }             String maxLabel = null;             int temp = 0;             for (Entry<String, Integer> iter : tempMap.entrySet()) {                 if (temp < iter.getValue()) {                     temp = iter.getValue();                     maxLabel = iter.getKey();                 }             }             labelMap.put(cid, maxLabel);         }           for (Point p : dataset) {             p.predictLabel = labelMap.get(p.cid);         }     }       /**      * 计算数据点之间的距离      *      * @param a 数据的坐标      * @param b 另一个数据的坐标      * @return      */     private double distance(double[] a, double[] b) {         if (a.length != b.length) {             throw new IllegalArgumentException("Arrry a not equal array b!");         }         double sum = 0;         for (int i = 0; i < a.length; i++) {             double dp = a[i] - b[i];             sum += dp * dp;         }         return (double) Math.sqrt(sum);     }         /**      * 读取数据集<br>      * 将数据集保存到数据集中      *      * @param fileName 文件名      * @param split 分隔符      * @param labelAtHead 标签是否在头部      * @throws IOException      */     public void importDataWithLabel(String fileName, String split,             boolean labelAtHead) throws IOException {         int dimensionNum = 0;         List<Point> dataList = new ArrayList<Point>();         // 读取数据文件         BufferedReader reader = new BufferedReader(new FileReader(fileName));         String line = null;         while ((line = reader.readLine()) != null) {             if (line.trim().equals("")) {                 continue;             }             // 字符串以split拆分             String[] splitStrs = line.split(split);             dimensionNum = splitStrs.length - 1;             double[] temp = new double[dimensionNum];               String label = splitStrs[dimensionNum];             if (labelAtHead) {                 label = splitStrs[0];                 for (int i = 0; i < dimensionNum; i++) {                     temp[i] = Double.parseDouble(splitStrs[i + 1]);                 }             } else {                 for (int i = 0; i < dimensionNum; i++) {                     temp[i] = Double.parseDouble(splitStrs[i]);                 }             }             dataList.add(new Point(temp, label));             dataNum++;         }         reader.close();         Collections.shuffle(dataList);         dataset = new Point[dataList.size()];         dataList.toArray(dataset);     }       /**      * 打印输出聚类信息      */     public void printInfo() {         System.out.println("迭代次数:" + maxIterNum);         System.out.println("聚类数目为:" + exemplar.size());         for (int j = 0; j < exemplar.size(); j++) {             System.out.println(j + ": " + exemplar.get(j));         }         for (Point point : dataset) {             System.out.println(point);         }     }         static class Point {         // 数据标签         private String label;         // 聚类预测的标签         private String predictLabel;         // 数据点所属簇id         private int cid;         // 数据点的维度         private double dimensioin[];           public Point(double dimensioin[], String label) {             this.label = label;             init(dimensioin);         }           public Point(double dimensioin[]) {             init(dimensioin);         }           public void init(double value[]) {             dimensioin = new double[value.length];             for (int i = 0; i < value.length; i++) {                 dimensioin[i] = value[i];             }         }           @Override         public String toString() {             return "Point [label=" + label + ", predictLabel=" + predictLabel                     + ", cid=" + cid + ", dimensioin="                     + Arrays.toString(dimensioin) + "]";         }       }   public static void main(String[] args) throws IOException {         AP ap = new AP(10000, 0.6);         ap.importDataWithLabel(FILEPATH, ",", false);         ap.init();         ap.clustering();         ap.printInfo();     } }