[数据结构]图的DFS和BFS的两种实现方式

深度优先搜索

深度优先搜索，我们以无向图为例。

图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。

它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

显然，深度优先搜索是一个递归的过程。

邻接矩阵DFS

package com.darrenchan.graph;

public class MatrixNDG {
    int size;//图顶点个数
    char[] vertexs;//图顶点名称
    int[][] matrix;//图关系矩阵

    public MatrixNDG(char[] vertexs, char[][] edges){
        size=vertexs.length;
        matrix=new int[size][size];//设定图关系矩阵大小
        this.vertexs=vertexs;

        for(char[] c:edges){//设置矩阵值
            int p1 = getPosition(c[0]);//根据顶点名称确定对应矩阵下标
            int p2 = getPosition(c[1]);

            matrix[p1][p2] = 1;//无向图，在两个对称位置存储
            matrix[p2][p1] = 1;
        }
    }

    //图的遍历输出
    public void print(){
        for(int[] i:matrix){
            for(int j:i){
                System.out.print(j+" ");
            }
            System.out.println();
        }
    }

    //根据顶点名称获取对应的矩阵下标
    private int getPosition(char ch) {
        for(int i=0; i<vertexs.length; i++)
            if(vertexs[i]==ch)
                return i;
        return -1;
    }

    public static void main(String[] args) {
        char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
        char[][] edges = new char[][]{
                {'A', 'C'},
                {'A', 'D'},
                {'A', 'F'},
                {'B', 'C'},
                {'C', 'D'},
                {'E', 'G'},
                {'D', 'G'},
                {'I', 'J'},
                {'J', 'G'},
                {'E', 'H'},
                {'H', 'K'}};
        MatrixNDG pG = new MatrixNDG(vexs, edges);
        pG.print();
        pG.DFS();
    }

    public void DFS(){
        boolean[] beTraversed=new boolean[size];
        for(int i=0;i<size;i++){
            beTraversed[i]=false;
        }
        System.out.print(vertexs[0] + " ");
        beTraversed[0]=true;
        DFS(0,0,beTraversed);
    }

    private void DFS(int x,int y,boolean[] beTraversed){
        while(y<=size-1){
            if(matrix[x][y]!=0&beTraversed[y]==false){
                System.out.print(vertexs[y] + " ");
                beTraversed[y]=true;
                DFS(y,0,beTraversed);
            }
            y++;
        }
    }
}

邻接表DFS

package com.darrenchan.graph;

public class ListNDG {
    Vertex[] vertexLists;//邻接表数组
    int size;

    class Vertex{//邻接表节点类，单链表数据结构
        char ch;
        Vertex next;

        Vertex(char ch){//初始化方法
            this.ch=ch;
        }
        void add(char ch){//加到链表尾
            Vertex node=this;
            while(node.next!=null){
                node=node.next;
            }
            node.next=new Vertex(ch);
        }
    }

    public ListNDG(char[] vertexs,char[][] edges){

        size=vertexs.length;
        this.vertexLists=new Vertex[size];//确定邻接表大小
        //设置邻接表每一个节点
        for(int i=0;i<size;i++){
            this.vertexLists[i]=new Vertex(vertexs[i]);
        }
        //存储边信息
        for(char[] c:edges){
            int p1=getPosition(c[0]);
            vertexLists[p1].add(c[1]);
            int p2=getPosition(c[1]);
            vertexLists[p2].add(c[0]);
        }

    }

    //跟据顶点名称获取链表下标
    private int getPosition(char ch) {
        for(int i=0; i<size; i++)
            if(vertexLists[i].ch==ch)
                return i;
        return -1;
    }

    //遍历输出邻接表
    public void print(){
        for(int i=0;i<size;i++){
            Vertex temp=vertexLists[i];
            while(temp!=null){
                System.out.print(temp.ch+" ");
                temp=temp.next;
            }
            System.out.println();
        }
    }

    public static void main(String[] args){
        char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
        char[][] edges = new char[][]{
                {'A', 'C'},
                {'A', 'D'},
                {'A', 'F'},
                {'B', 'C'},
                {'C', 'D'},
                {'E', 'G'},
                {'D', 'G'},
                {'I', 'J'},
                {'J', 'G'},
                {'E', 'H'},
                {'H', 'K'}};

        ListNDG pG = new ListNDG(vexs, edges);
        pG.print();   // 打印图
        pG.DFS();
    }

    public void DFS(){
        boolean[] beTraversed=new boolean[size];
        for(int i=0;i<size;i++){
            beTraversed[i]=false;
        }
        for (int i = 0; i < size; i++) {
            if (!beTraversed[i])
                DFS(beTraversed,vertexLists[i]);
        }

    }

    public void DFS(boolean[] beTraversed,Vertex temp){

        System.out.print(temp.ch + " ");
        beTraversed[getPosition(temp.ch)]=true;

        while(temp!=null){
            if(beTraversed[getPosition(temp.ch)]==false){
                DFS(beTraversed,vertexLists[getPosition(temp.ch)]);
            }
            temp=temp.next;
        }

    }
}

广度优先搜索

广度优先搜索，我们以有向图为例。

广度优先搜索算法(Breadth First Search)，又称为”宽度优先搜索”或”横向优先搜索”，简称BFS。

它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2…的顶点。

邻接矩阵BFS

package com.darrenchan.graph;

import java.util.LinkedList;

public class MatrixDG {
    int size;
    char[] vertexs;
    int[][] matrix;

    public MatrixDG(char[] vertexs,char[][] edges){
        size=vertexs.length;
        matrix=new int[size][size];
        this.vertexs=vertexs;

        //和邻接矩阵无向图差别仅仅在这里
        for(char[] c:edges){
            int p1 = getPosition(c[0]);
            int p2 = getPosition(c[1]);

            matrix[p1][p2] = 1;
        }

    }

    public void print(){
        for(int[] i:matrix){
            for(int j:i){
                System.out.print(j+" ");
            }
            System.out.println();
        }
    }

    private int getPosition(char ch) {
        for(int i=0; i<vertexs.length; i++)
            if(vertexs[i]==ch)
                return i;
        return -1;
    }

    public static void main(String[] args) {
        char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
        char[][] edges = new char[][]{
                {'A', 'C'},
                {'A', 'D'},
                {'A', 'F'},
                {'B', 'C'},
                {'C', 'D'},
                {'E', 'G'},
                {'D', 'G'},
                {'I', 'J'},
                {'J', 'G'},
                {'E', 'H'},
                {'H', 'K'}};
        MatrixDG pG = new MatrixDG(vexs, edges);
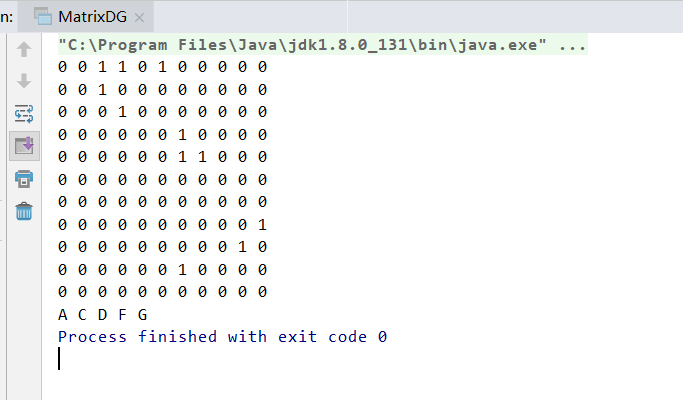
        pG.print();
        pG.BFS();
    }

    public void BFS(){
        boolean[] beTraversed=new boolean[size];
        for(int i=0;i<size;i++){
            beTraversed[i]=false;
        }
        System.out.print(vertexs[0] + " ");
        beTraversed[0]=true;
        BFS(0,beTraversed);
    }

    public void BFS(int x,boolean[] beTraversed){
        LinkedList<Character> list=new LinkedList<Character>();
        int y=0;
        while(y<=size-1){
            if(matrix[x][y]!=0&beTraversed[y]==false){
                System.out.print(vertexs[y] + " ");
                beTraversed[y]=true;
                list.add(vertexs[y]);
            }
            y++;
        }
        while(!list.isEmpty()){
            char ch=list.pop();
            int t=getPosition(ch);
            BFS(t,beTraversed);
        }
    }

}

邻接表BFS

package com.darrenchan.graph;

import java.util.LinkedList;

public class ListDG {
    Vertex[] vertexLists;
    int size;

    class Vertex{
        char ch;
        Vertex next;

        Vertex(char ch){
            this.ch=ch;
        }
        void add(char ch){
            Vertex node=this;
            while(node.next!=null){
                node=node.next;
            }
            node.next=new Vertex(ch);
        }

    }

    public ListDG(char[] vertexs,char[][] edges){

        size=vertexs.length;
        this.vertexLists=new Vertex[size];
        //设置邻接表每一个节点
        for(int i=0;i<size;i++){
            this.vertexLists[i]=new Vertex(vertexs[i]);
        }
        //存储边信息
        //只有这里和无序图不同
        for(char[] c:edges){
            int p=getPosition(c[0]);
            vertexLists[p].add(c[1]);
        }

    }

    private int getPosition(char ch) {
        for(int i=0; i<size; i++)
            if(vertexLists[i].ch==ch)
                return i;
        return -1;
    }

    public void print(){
        for(int i=0;i<size;i++){
            Vertex temp=vertexLists[i];
            while(temp!=null){
                System.out.print(temp.ch+" ");
                temp=temp.next;
            }
            System.out.println();
        }
    }

    public static void main(String[] args){
        char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
        char[][] edges = new char[][]{
                {'A', 'C'},
                {'A', 'D'},
                {'A', 'F'},
                {'B', 'C'},
                {'C', 'D'},
                {'E', 'G'},
                {'D', 'G'},
                {'I', 'J'},
                {'J', 'G'},
                {'E', 'H'},
                {'H', 'K'}};

        ListDG pG = new ListDG(vexs, edges);
        pG.print();   // 打印图
        pG.BFS();
    }

    public void BFS(){
        boolean[] isTraversed=new boolean[size];
        for(int i=0;i<size;i++){
            isTraversed[i]=false;
        }
        System.out.print(vertexLists[0].ch + " ");
        isTraversed[0]=true;
        BFS(0,isTraversed);
    }

    public void BFS(int x,boolean[] isTraversed){
        Vertex temp=vertexLists[x];
        LinkedList<Vertex> list=new LinkedList<Vertex>();
        while(temp!=null){
            if(isTraversed[getPosition(temp.ch)]==false){
                System.out.print(temp.ch + " ");
                isTraversed[getPosition(temp.ch)]=true;
                list.add(temp);
            }
            temp=temp.next;
        }
        while(!list.isEmpty()){
            Vertex v=list.pop();
            int t=getPosition(v.ch);
            BFS(t,isTraversed);
        }
    }
}

参考：https://blog.csdn.net/picway/article/details/68483894