POJ 1061 - 青蛙的约会 - [exgcd求解一元线性同余方程]

先上干货：

定理1：

如果d = gcd(a,b)，则必能找到正的或负的整数k和l，使ax + by = d.

（参考exgcd：http://www.cnblogs.com/dilthey/p/6804137.html）

定理2：

一元线性同余方程ax ≡ n (mod b) 有解，当且仅当gcd(a,b)|n.

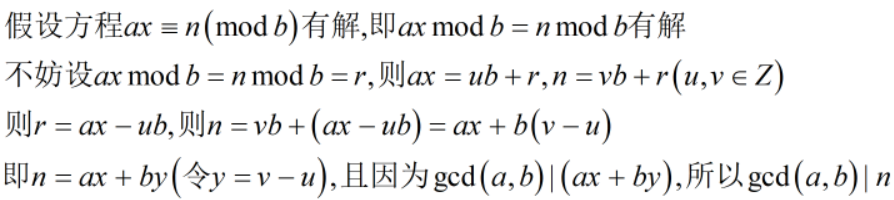
也就是说，解出了ax+by=gcd(a,b)，就相当于解出了ax≡n(mod b) （而且只要满足gcd(a,b)|n，就一定有解）

定理3：

若gcd(a,b) = 1，则方程ax ≡ n (mod b)在[0, b-1]上有唯一解.

由上可知ax ≡ n (mod b) 即方程 ax + by = n，由定理1可知必然存在x,y满足 ax + by = gcd(a,b) = 1，则必然存在nx,ny满足 ax + by = n

则必然ax ≡ n (mod b)有解nx，由于nx+kb都是该方程的解，则在[0, b-1]上必然出现一个解。

再证唯一性：

唯一满足mod b = 0的条件的，只有x1 = x2

定理4：

若gcd(a, b) = d，则方程ax ≡ n (mod b)在[0, b/d - 1]上有唯一解.

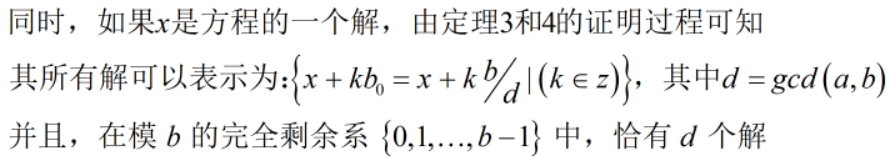
这样，如果我有一个方程ax ≡ n (mod b)的任意解X，那么我先X mod (b/d)，使得其在范围[-b/d+1,b/d-1]范围内，

再加上b/d就使其在范围[1,2(b/d)-1]范围内，再mod (b/d)就可以使其处在[0,b/d -1]范围内了。

即在[0,b/d-1]范围内的解x=[ X mod (b/d) + (b/d) ] mod (b/d).

分割线

然后正式关于题目：

题目链接：http://poj.org/problem?id=1061

题解：

青蛙A：a = ( x + mt ) mod L

青蛙B：b = ( y + nt ) mod L

现在要使得a=b，即( x + mt ) = ( y + nt ) (mod L)，即( x - y ) + ( m - n ) t = kL；

即求最小的正整数t满足 ( m - n ) t + KL = y - x （K=-k），即求一元线性同余方程( m - n ) x ≡ ( y - x ) (mod L) 的解；

那么就像上面那样，先算( m - n ) * x + L * K = gcd( m - n , L )，得到一个x的值；

然后判断( y - x ) mod gcd( m - n , L ) == 0 ?，若能整除，则有解；

然后就只要先把x *= ( y - x ) / gcd( m - n , L ) ，再根据上面求出解集中的最小正整数即为答案；

PS.当然，最后一步求[0,b/d-1]范围内的唯一解时，由于要mod (b/d)，我们要保证b/d为正，在本题中，即保证L/d为正，故d要为正。

AC代码：

 #include<cstdio>
 #include<algorithm>
 typedef long long ll;
 using namespace std;
 ll x,y,m,n,L;
 ll d,ans,K;
 void exgcd(ll a,ll b,ll &d,ll &x,ll &y){
     if(!b){d=a;x=;y=;}
     else {exgcd(b,a%b,d,y,x);y-=(a/b)*x;}
 }
 int main()
 {
     scanf("%lld%lld%lld%lld%lld",&x,&y,&m,&n,&L);
     if(m<n)
     {
         swap(m,n);
         swap(x,y);
     }
     exgcd(m-n,L,d,ans,K);
     if(d== || (x-y)%d!=) printf("Impossible\n");
     else
     {
         ans*=(y-x)/d;
         ans=(ans%(L/d)+(L/d))%(L/d);
         printf("%I64d\n",ans);
     }
 }

PS.曾经刚开始搞ACM的时候，就因为这题是POJ第一页上为数不多的中文题而钻了很久，不过以当时的实力，想想就知道怎么磕都磕不出来的，今天总算把这道题给补上了，感觉还是不错的