非参数估计——核密度估计（Parzen窗）

　　核密度估计，或Parzen窗，是非参数估计概率密度的一种。比如机器学习中还有K近邻法也是非参估计的一种，不过K近邻通常是用来判别样本类别的，就是把样本空间每个点划分为与其最接近的K个训练抽样中，占比最高的类别。

直方图

　　首先从直方图切入。对于随机变量$X$的一组抽样，即使$X$的值是连续的，我们也可以划分出若干宽度相同的区间，统计这组样本在各个区间的频率，并画出直方图。下图是均值为0，方差为2.5的正态分布。从分布中分别抽样了100000和10000个样本：

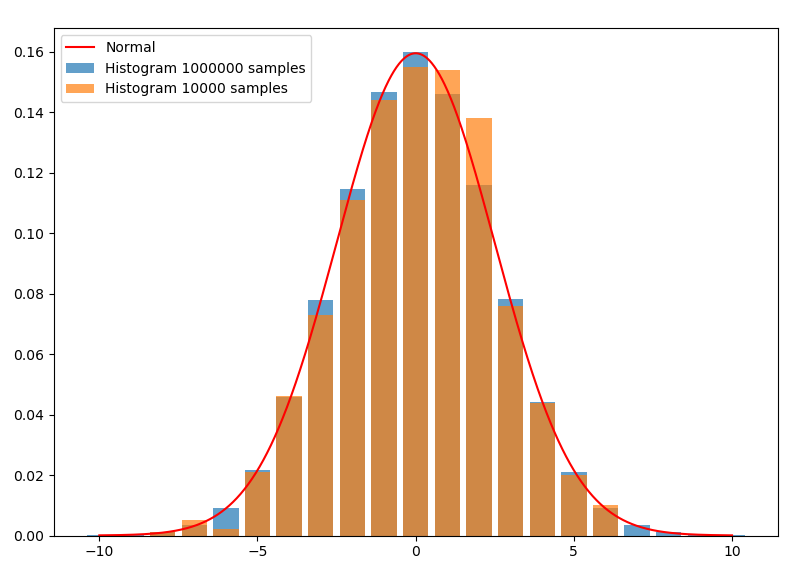
　　这里的直方图离散地取了21个相互无交集的区间：$[x-0.5,x+0.5), x=-10,-9,...,10$，单边间隔$h=0.5$。$h>0$在核函数估计中通常称作带宽，或窗口。每个长条的面积就是样本在这个区间内的频率。如果用频率当做概率，则面积除以区间宽度后的高，就是拟合出的在这个区间内的平均概率密度。因为这里取的区间宽度是1，所以高与面积在数值上相同，使得长条的顶端正好与密度函数曲线相契合。如果将区间中的$x$取成任意值，就可以拟合出实数域内的概率密度（其中$N_x$为样本$x_i\in [x-h,x+h),i=1,...,N$的样本数）：

$\displaystyle\hat{f}(x)=\frac{N_x}{N}\cdot\frac{1}{2h}$

　　这就已经是核函数估计的一种了。显然，抽样越多，这个平均概率密度能拟合得越好，正如蓝条中上方几乎都与曲线契合，而橙色则稂莠不齐。另外，如果抽样数$N\to \infty$，对$h$取极限$h\to 0$，拟合出的概率密度应该会更接近真实概率密度。但是，由于抽样的数量总是有限的，无限小的$h$将导致只有在抽样点处，才有频率$1/N$，而其它地方频率全为0，所以$h$不能无限小。相反，$h$太大的话又不能有效地将抽样量用起来。所以这两者之间应该有一个最优的$h$，能充分利用抽样来拟合概率密度曲线。容易推理出，$h$应该和抽样量$N$有关，而且应该与$N$成反比。

核函数估计

　　为了便于拓展，将拟合概率密度的式子进行变换：

$\displaystyle\hat{f}(x)=\frac{N_x}{2hN} = \frac{1}{hN}\sum\limits_{i=1}^{N}\begin{cases}1/2& x-h\le x_i < x+h\\ 0& else \end{cases}$

$\displaystyle = \frac{1}{hN}\sum\limits_{i=1}^{N}\begin{cases} 1/2,& -1\le \displaystyle\frac{x_i-x}{h} < 1\\ 0,& else \end{cases}$

$\displaystyle = \frac{1}{hN}\sum\limits_{i=1}^{N}\displaystyle K(\frac{x_i-x}{h}),\;\; where \; K(x) =\begin{cases} 1/2,& -1\le x < 1\\ 0,& else \end{cases}$

　　得到的$K(x)$就是uniform核函数（也又叫方形窗口函数），这是最简单最常用的核函数。形象地理解上式求和部分，就是样本出现在$x$邻域内部的加权频数（因为除以了2，所以所谓“加权”）。核函数有很多，常见的还有高斯核函数（高斯窗口函数），即：

$\displaystyle K(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2}$

　　各种核函数如下图所示：

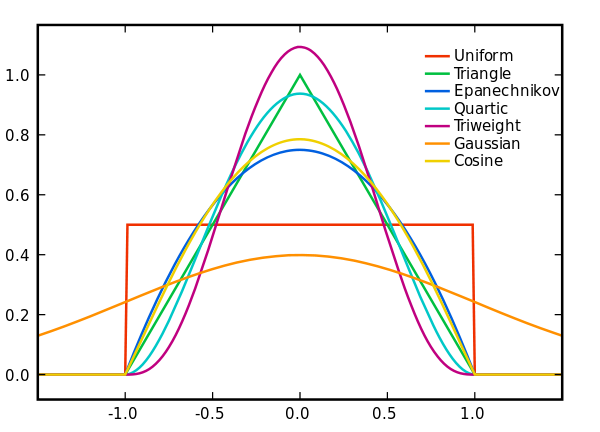
核函数的条件

　　并不是所有函数都能作为核函数的，因为$\hat{f}(x)$是概率密度，则它的积分应该为1，即：

$\displaystyle\int\limits_{R}\hat{f}(x) dx = \int\limits_{R}\frac{1}{hN}\sum\limits_{i=1}^{N} K(\frac{x_i-x}{h})dx =\frac{1}{hN}\sum\limits_{i=1}^{N} \int_{-\infty}^{\infty} K(\frac{x_i-x}{h})dx$

　　令$\displaystyle t = \frac{x_i-x}{h}$

$\displaystyle =\frac{1}{N}\sum\limits_{i=1}^{N} \int_{\infty}^{-\infty} -K(t)dt$

$\displaystyle=\frac{1}{N}\sum\limits_{i=1}^{N} \int_{-\infty}^{\infty} K(t)dt=1$

　　因积分部分为定值，所以可得$K(x)$需要的条件是：

$\displaystyle\int_{-\infty}^{\infty} K(x)dx=1$

　　通常$K(x)$是偶函数，而且不能小于0，否则就不符合实际了。

带宽选择与核函数优劣

　　正如前面提到的，带宽$h$的大小关系到拟合的精度。对于方形核函数，$N\to \infty$时，$h$通常取收敛速度小于$1/N$的值即可，如$h=1/\sqrt{N}$。对于高斯核，有证明指出$\displaystyle h=\left (  \frac{4 \hat{\sigma}^5 }{3N} \right )^{\frac{1}{5}}$时，有较优的拟合效果（$\hat{\sigma}^2$是样本方差）。具体的带宽选择还有更深入的算法，具体问题还是要具体分析，就先不细究了。使用高斯核时，待拟合的概率密度应该近似于高斯分布那样连续平滑的分布，如果是像均匀分布那样有明显分块的分布，拟合的效果会很差。我认为原因应该是它将离得很远的样本也用于拟合，导致本该突兀的地方都被均匀化了。

　　Epanechnikov在均方误差的意义下拟合效果是最好的。这也很符合直觉，越接近$x$的样本的权重本应该越高，而且超出带宽的样本权重直接为0也是符合常理的，它融合了均匀核与高斯核的优点。

多维情况

　　对于多维情况，假设随机变量$X$为$m$维（即$m$维向量），则拟合概率密度是$m$维的联合概率密度：

$\displaystyle \hat{f}(x)= \frac{1}{h^mN}\sum\limits_{i=1}^{N}\displaystyle K(\frac{x_i-x}{h})$

　　其中的$K(x)$也变成了$m$维的联合概率密度。另外，既然$\displaystyle\frac{1}{N}\sum\limits_{i=1}^{N} K(\frac{x_i-x}{h})$代表的是概率，$m$维的概率密度自然是概率除以$h^m$而不是$h$。

实验拟合情况