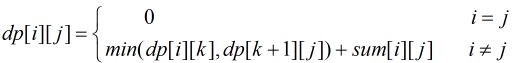DP之石子堆合并问题

• 相邻
• 环形

• 总结

（1）相邻：在一个圆形操场的四周摆放着n堆石子(n<= 100)，现要将石子有次序地合并成一堆。规定每次只能选取相邻的两堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。选择一种合并石子的方案，使得做n－1次合并，得分的总和最小。

 /*
      * 在一个圆形操场的四周摆放着n堆石子(n<= 100)，现要将石子有次序地合并成一堆。
      * 规定每次只能选取相邻的两堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。
      *选择一种合并石子的方案，使得做n－1次合并，得分的总和最小。
      */
     public static void test(int[]a) {
         //b[i][j]表示i-j相加之和，求出每一斜列的最小值就是这一步相加
         int[][]b=new int[a.length][a.length];
         //赋初值
         for(int i=0;i<a.length;i++) {
             b[i][i]=a[i];
             System.out.print(a[i]+" ");
         }
         int sum=0;
         System.out.println("score:"+sum);
         for(int r=1;r<=a.length-1;r++) {
             int min=b[1][r]+b[0][0];
             int index1=0,index2=r;
             b[0][r]=min;
             for(int i=1;i<a.length-r;i++) {
                 int j=i+r;
                 b[i][j]=b[i+1][j]+b[i][i];
                 if(b[i][j]<min) {
                     min=b[i][j];
                     index1=i;
                     index2=j;
                 }
             }

             for(int i=0;i<a.length;i++) {
                 if(i<index1||i>index2) {
                     System.out.print(a[i]+" ");
                 }else if(i==index1){//出现最小值
                     System.out.print(min+" ");
                 }
             }
             sum+=min;
             System.out.println("score:"+sum);
         }
     }

思路就是类似矩阵连乘，关键就是最优解不好表示或者我写的有问题。。。（明天再来改！！！今天累了）Ok得出结论了就是我的想法有问题。

下面是标准DP：

设dp[i][j]表示第i到第j堆石子合并的最优值（合并i-j的花费的最小力气），sum[i][j]表示第i到第j堆石子的总数量。那么就有状态转移公式： 

因为每一个石子堆无非是和左边合并或者先和右边合并。对第i到第j的每一个k（子问题）计算他们的最小值加上每堆石子的总数量因为最后一步总是把所有的都合并。

我们可以从最小问题想起来：假如这个数组只有三个数，那么最小力气就是min(左边两个,右边两个)+三个的总量（最后一步）

有四个数时，将它们分为1-3，2-4两个子问题再继续分...

 public static void testA(int[]a) {
         class Point{
             int start;
             int end;
             public Point(int start, int end) {
                 this.start = start;
                 this.end = end;
             }
         }
         //b[i][j]表示第i堆到第j堆的最优合并值
         int[][]b=new int[a.length][a.length];
         //s表示i到j的和
         int[][]s=new int[a.length][a.length];
         //保存最优解 0左 1下
         int[][]l=new int[a.length][a.length];
         Stack<Point> stack=new Stack<Point>();
         //赋初值
         for(int i=0;i<a.length;i++) {
             b[i][i]=0;
             s[i][i]=a[i];
         }

         for(int r=1;r<=a.length-1;r++) {
             for(int i=0;i<a.length-r;i++) {
                 int j=i+r;
                 s[i][j]=s[i][j-1]+s[j][j];
                 if(b[i][j-1]<b[i+1][j]) {//左边小
                     b[i][j]=b[i][j-1]+s[i][j];
                     l[i][j]=0;
                 }else {//下边小
                     b[i][j]=b[i+1][j]+s[i][j];
                     l[i][j]=1;
                 }
             }
         }
         int x=0,y=a.length-1;
         for(int i=0;i<a.length;i++) {
             stack.add(new Point(x,y));
             if(l[x][y]==0)//左边
                 y--;
             else
                 x++;
         }

         while(!stack.isEmpty()) {
             Point p=stack.pop();
             for(int i=0;i<a.length;i++) {
                 if(i<p.start||i>p.end)
                     System.out.print(a[i]+" ");
                 else if(i==p.start)
                     System.out.print(s[p.start][p.end]+" ");
             }
             System.out.println("score:"+b[p.start][p.end]);
         }
     }

（2）环形：就是不是相邻的是成环的

最简单的就是穷举相邻的找出最小的。这个时候把上面函数的返回值设为int然后计算。

第二种方法是将两边各扩展一位。因为只和左右相关边界位置应与头尾相连，然后进行相同的计算，最后在几种方案中挑出最小的。

 public static void testB(int[]a) {
         class Point{
             int start;
             int end;
             public Point(int start, int end) {
                 this.start = start;
                 this.end = end;
             }
         }
         //首尾相连
         int[]b=new int[a.length+2];
         b[0]=a[a.length-1];
         b[b.length-1]=a[0];
         for(int i=0;i<a.length;i++) {
             b[i+1]=a[i];
         }

         //i-j的最优
         int[][]d=new int[b.length][b.length];
         //sum
         int[][]s=new int[b.length][b.length];
         //最优解0左 1下
         int[][]l=new int[b.length][b.length];
         Stack<Point> stack=new Stack<Point>();
         //赋初值
         for(int i=0;i<b.length;i++) {
             d[i][i]=0;
             s[i][i]=b[i];
         }
         //可以不填满,只填到需要的就行
         int min=-1;
         Point end=new Point(-1,-1);
         for(int r=1;r<=a.length-1;r++) {
             for(int i=0;i<b.length-r;i++) {
                 int j=i+r;
                 s[i][j]=s[i][j-1]+s[j][j];
                 if(d[i][j-1]<d[i+1][j]) {//左边
                     d[i][j]=d[i][j-1]+s[i][j];
                     l[i][j]=0;
                 }else {//下边
                     d[i][j]=d[i+1][j]+s[i][j];
                     l[i][j]=1;
                 }
                 if(r==a.length-1) {//找到最小的那个的值并记录解
                     if(min==-1)
                         {
                         min=d[i][j];
                         end.start=i;
                         end.end=j;
                         }
                     else if(min>d[i][j])
                         {
                         min=d[i][j];
                         end.start=i;
                         end.end=j;
                         }
                 }
             }
         }
         int x=end.start,y=end.end;
         for(int i=0;i<a.length;i++) {
             stack.add(new Point(x,y));
             if(l[x][y]==0)//左边
                 y--;
             else
                 x++;
         }
         while(!stack.isEmpty()) {
             Point p=stack.pop();
             for(int i=0;i<a.length;i++) {
                 if(i<p.start||i>p.end)
                     System.out.print(b[i]+" ");
                 else if(i==p.start)
                     System.out.print(s[p.start][p.end]+" ");
             }
             System.out.println("score:"+d[p.start][p.end]);
         }
     }

(3)总结

这个是典型的DP问题，因为已经处理过之前的矩阵连乘问题，所以一开始我陷入了固定思维只想着填表，而没有去找子问题一步一步来。本末倒置。导致思路很不清晰但是代码似乎更简短。在处理环形时，选取了在两边扩展一位再每次分组计算最后取出一部分。