LeetCode做题笔记之动态规划

LeetCode之动态规划

时间有限只做了下面这几道：70、338、877、96、120、95、647，后续会继续更新

70：爬楼梯

先来道简单的练练手，一道经典的动态规划题目

可以采用动态规划的备忘录法，第n节楼梯的数目等于第n-1节和n-2节的和，因为第n节一定由n-1或n-2上去的。可以不使用递归而使用简单的for循环实现：

public int climbStairs(int n) {
    int[] ints = new int[n + 1];
    ints[1] = 1;
    if (n > 1) ints[2] = 2;
    for (int i = 3; i <= n; i++) {
        ints[i] = ints[i - 1] + ints[i - 2];
    }
    return ints[n];
}

这道题的难点在于想到第n节的数目等于n-1和n-2节的数目，对于没有接触过动态规划的菜鸟来说还是有点意思的。

PS：如果数目过大超出了int类型的最大值，可以使用BigInteger类

338：比特位计数

这道题也还行，对二进制数来说，一个偶数的最后一位一定是0，基于这个原理可以得出下面的代码：

for (int i = 0; i < arr.length; i++) {
    if (i % 2 == 0) {
        arr[i] = arr[i / 2];
    }else {
        arr[i] = arr[i /2] + 1;
    }
}

然而~~大佬们总是有强大的方法，我那if else用一行代码就搞定了：arr[i] = arr[i >> 1] + (i & 1)，右移倒也还好，这个i & 1用的就简直了，佩服佩服。

话说这和动态规划没什么关系吧？可我是专门挑的动态规划的题做的欸

877：石子游戏

感觉这题出的不太好，因为我想看到的是你的算法比我的算法厉害，而不是你直接给我说先手必赢，因为我完全没有往这方面考虑过（估计大佬能想出来吧）。先手必赢的原因是先手可以决定拿所有的偶数堆还是奇数堆，而对偶数堆和奇数堆两个一定有一个是数目比较多的（总数为奇数）

最开始我觉得比较一下前后的的大小直接挑大的就行，但是对于[3,2,10,4]这样的排列先手会得7分而后手得12分，这显然是错误的。

这一题的思路是以局部最优解得出整体最优解，典型的动态规划

public static boolean stoneGame(int[] piles) {
    int length = piles.length;
    //results[i][j]存储的是piles中第i个数到第j个数组成序列的最佳拿取方式下的得分
    int[][] results = new int[length][length];
    //当集合中只有一个堆的时候，拿的那个人直接得分
    for(int i=0;i<length;i++){
        results[i][i]=piles[i];
    }
    //当集合中有两个数的时候，先选的人肯定是拿较大数,分数为max-min
    for(int i=0;i<length-1;i++){
        results[i][i+1]=Math.abs(piles[i]-piles[i+1]);
    }

    for(int i=length-3;i>=0;i--){
        for(int j=i+2;j<length;j++){
            results[i][j]=Math.max(piles[i]-results[i+1][j],piles[j]-results[i][j-1]);
        }
    }
    return results[0][length-1]>0;
}

对于二维数组results[i][j]：

第一个for循环计算的是绿色的方块，第二个for循环计算蓝色的方块，第三个填充右上的白色的方块

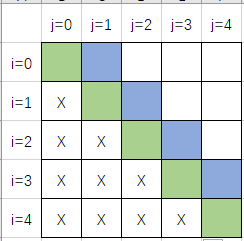
最后只要看右上角的值是否大于0即可。

96：不同的二叉搜索树

这一道题的难点在于找出节点增加时二叉搜索树种类如何增加。

首先，新增加的节点默认是最大的（不然没什么意义），对于n+1个节点的树来说，有C(n+1) = C0 * Cn + C1 * C(n-1) + ... + C(n-1) * C1 + Cn * C0其中C0 = 1, C1 = 1解释：对于第n+1个节点的树来说，C0 * Cn对应以最小节点为根节点，左节点为0个，右节点为n个；C1 * C(n-1)对应以倒数第二小的为根节点，左边1个节点，右边n-1个节点......直到第n+1个节点为子节点。这样的话代码就很容易写出来了。

public static int numTrees(int n) {
    if(n<=1)return 1;
    int[] dp=new int[n+1];
    dp[0]=1;
    dp[1]=1;
    for(int i=2;i<=n;i++){
        for(int j=1;j<=i;j++){
            dp[i]+=dp[j-1]*dp[i-j];
        }
    }
    return dp[n];
}

话说这道题根本和动态规划没多大关系啊，完全是在计算CatAlan数。。。

120：三角形最小路径和

这一题和第877题比较像，可以把三角形斜向左上，就像这样：



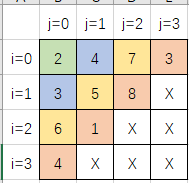
解法也和877比较像：

public static int minimumTotal(List<List<Integer>> triangle) {
    int[][] arr = new int[triangle.size()][triangle.size()];
    List<Integer> lastList = triangle.get(triangle.size() - 1);
    for (int i = 0; i < lastList.size(); i++) {
        arr[arr.length - 1 - i][i] = lastList.get(i);
    }

    for (int n = triangle.size() -2; n >= 0; n--) {
        List<Integer> list = triangle.get(n);
        for (int i = 0; i <= n; i++) {
            int j = n-i;
            arr[i][j] = list.get(j) + Math.min(arr[i + 1][j], arr[i][j + 1]);
        }
    }
    return arr[0][0];
}

然后再新建个一样的二维数组记录由该点到底部所需的最小和。

95：不同的二叉搜索树2

这一题是第96题的增强题，不仅要求求出多少个，还要求出每个什么样子。这一题其实最开始没解出来，看了答案之后才动了怎么做，原来是通过暴力递归（貌似也只能这么做了），题目做多了之后下意识地觉得肯定不是暴力解，总想着找一种更省力的方法，然而有时候就是会陷入其中。

private static List<TreeNode> helper(int start, int end) {
    List<TreeNode> res = new ArrayList<>();
    if (start > end) {
        res.add(null);
        return res;
    }
    for (int val = start; val <= end; val++) {
        List<TreeNode> left = helper(start, val - 1);
        List<TreeNode> right = helper(val + 1, end);
        for (TreeNode l : left) {
            for (TreeNode r : right) {
                TreeNode root = new TreeNode(val);
                root.left = l;
                root.right = r;
                res.add(root);
            }
        }
    }
    return res;
}

647：回文子串

最开始看到这一题时想到了第五题：最长回文子串，然后想到了Manacher（马拉车）算法，马拉车的数组P[]既然可以求出最长回文子串，那么就能求出回文子串的个数：

//此方法对字符串进行加工
public static String preProcess(String s) {
    StringBuilder sb = new StringBuilder(s.length()*2+3);
    sb.append("^");
    for (int i = 0; i < s.length(); i++) {
        sb.append("#").append(s.charAt(i));
    }
    sb.append("#$");
    return sb.toString();
}

// 马拉车算法
public static int countSubstrings(String s) {
    String T = preProcess(s);
//        System.out.println(Arrays.toString(T.toCharArray()));
    int n = T.length();
    int[] P = new int[n];
    int C = 0, R = 0;
    for (int i = 1; i < n - 1; i++) {
        int i_mirror = 2 * C - i;
        if (R > i) {
            P[i] = Math.min(R - i, P[i_mirror]);// 防止超出 R
        } else {
            P[i] = 0;// 等于 R 的情况
        }

        // 碰到之前讲的三种情况时候，需要继续扩展
        while (T.charAt(i + 1 + P[i]) == T.charAt(i - 1 - P[i])) {
            P[i]++;
        }

        // 判断是否需要更新 R
        if (i + P[i] > R) {
            C = i;
            R = i + P[i];
        }
    }
    //此时P[]数组已经求出，根据该数组可以获得回文子串的个数
    int sum = 0;
    for (int i = 1; i < P.length - 1; i++) {
        if (i % 2 == 0) {
            sum += (P[i] + 1) / 2;
        } else {
            sum += P[i] / 2;
        }
    }
//        System.out.println(Arrays.toString(P));
    return sum;
}

结果一看评论全都是用的两边扫描……我就纳闷了，做第五题的时候都在马拉车，就我两边扫描，结果到这题了都是两边扫描就我马拉车，难道我思维比较奇葩？

贴个中心扫描的答案：

public int countSubstrings2(String s) {
    for (int i=0; i < s.length(); i++){
        count(s, i, i);//回文串长度为奇数
        count(s, i, i+1);//回文串长度为偶数
    }
    return num;
}

public void count(String s, int start, int end){
    while(start >= 0 && end < s.length() && s.charAt(start) == s.charAt(end)){
        num++;
        start--;
        end++;
    }
}

┓(;´_｀)┏