手写实现java栈结构，并实现简易的计算器（基于后缀算法）

　　一、定义

　　栈是一种线性表结构，栈结构中有两端，对栈的操作都是对栈的一端进行操作的，那么被操作的一端称为栈顶，另一端则为栈底。对栈的操作其实就是只有两种，分别是入栈（也称为压栈）和出栈（也称为弹栈）。入栈，将新元素压入栈中，那么此时这个栈元素就成为了栈顶元素，栈深度相应的+1。出栈，将栈中的栈顶元素弹出来，此时栈顶的下一个元素就会成为新的栈顶元素，栈深度也相应的-1。根据入栈和出栈的规则，也可以得到栈数据的顺序是后进先出（LIFO,LAST IN FIRST OUT）的特性。栈结构的效率是非常高的，因此无论栈中数据的量有多大，操作的也只有栈顶元素一个数据，因此栈的时间复杂度为O（1）,这里不考虑栈溢出扩容的问题。栈结构示意图下图：

　　二、栈的应用场景

　　栈的数据接口在编程中的应用是非常广泛的，其中包括：

　　1、浏览器页面的浏览记录。我们在浏览器中浏览的页面的时候后退和前进能够正确的跳转到对应的页面，就是利用了栈的特性来实现的。

　　2、java虚拟机中栈的操作数栈也是利用栈实现的。java在编译的时候讲操作的代码压入操作数栈中，进行运算时就将栈顶元素弹出来，然后进行运算后将结果再压进操作数栈中。

　　3、计算器的实现。我们在计算的时候一般都是从左往右计算的，但是这种方式对于计算机是非常不友好的，它需要进行大量的判断才可以。但是利用栈以及一些算法就能轻松实现计算的功能。我们下面的例子也将会利用栈结构来实现简易的计算器的功能。

　　三、入栈和出栈

　　栈结构可以使用数组结构和链表结构来实现，因此不同的实现方式，入栈和出栈的实现方式也会有所区别。基于数组实现的栈的入栈和出栈操作实质是在内部维护了一个指针，这个指针指向的元素即为栈顶元素，入栈时讲指针向上移动一位，相反地则向下移动一位。基于链表的栈就没有了指针的概念。链表使用单向链表即可实现。链表的出栈和入栈实质上维护的链表头部元素。下面使用示意图来简单的演示一下两种结构的入栈和出栈的流程：

　　1、基于数组的入栈和出栈：

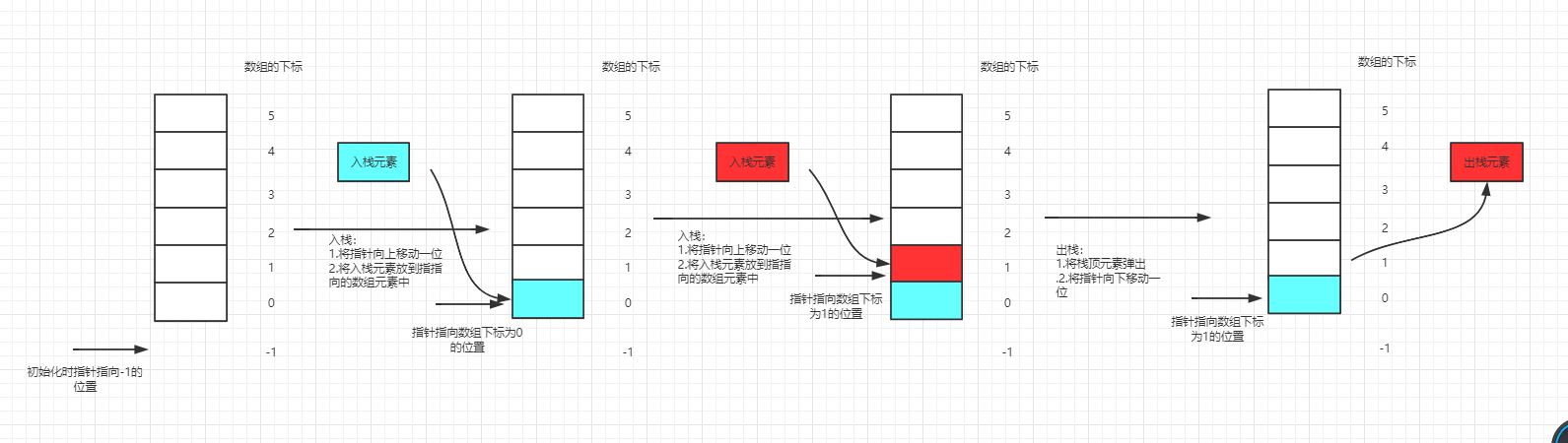
　　2.链表的入栈和出栈

　　

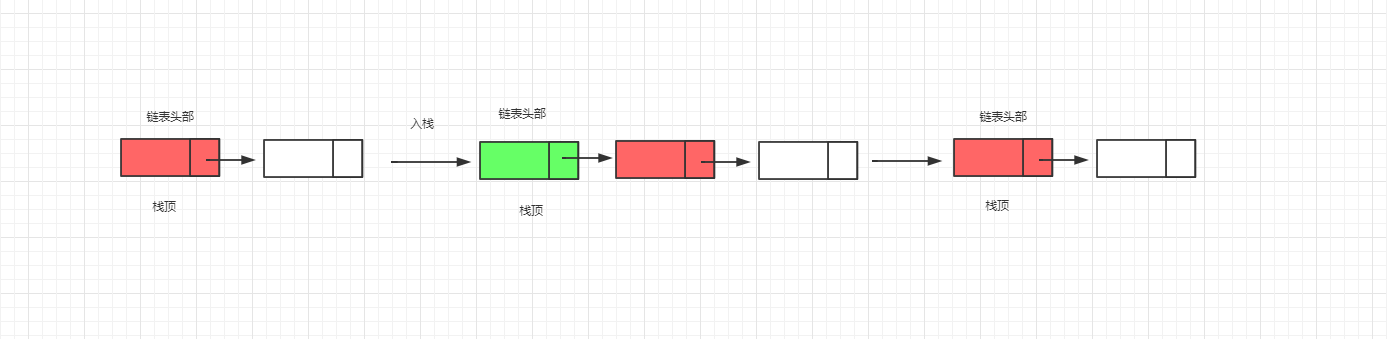
　　四、代码实现

　　1.数组

/**
 * 基于数组实现的栈
 */
public class ArrayStack<E> implements Stack<E> {

    private Object[] data;
    private int index = -1;
    private int deep;
    private static final int DEFAULT_CAPACITY = 1 << 4;

    public ArrayStack() {
        deep = DEFAULT_CAPACITY;
        data = new Object[deep];
    }

    public ArrayStack(int capacity) {
        if (capacity <= 0) {
            capacity = DEFAULT_CAPACITY;
        }
        deep = capacity;
        data = new Object[deep];
    }

    /**
     * 添加数据，数组满了就不添加
     * @param e 入栈元素
     * @return
     */
    @Override
    public E push(E e) {
        if (isFull()) {
            System.out.println("栈已满");
            return null;
        }
        data[++index] = e;
        return e;
    }

    /**
     * 弹出元素
     * @return 栈顶元素
     */
    @Override
    public E pop() {
        if (isEmpty()) {
            System.out.println("栈为空");
            return null;
        }
        return (E) data[index--];
    }

    /**
     * 查看栈顶元素
     * @return
     */
    @Override
    public E peek() {
        if (isEmpty()) {
            System.out.println("栈为空");
            return null;
        }
        return (E) data[index];
    }

    /**
     * 栈深度
     * @return
     */
    @Override
    public int size() {
        return index + 1;
    }

    private boolean isEmpty() {
        return index <= -1;
    }

    private boolean isFull() {
        return deep == index + 1;
    }

　　2.链表

/**
 * 基于链表实现的栈
 * @param <E>
 */
public class LinkStack<E> implements Stack<E> {

    private Node<E> head;
    private int size;

    @Override
    public E push(E e) {
        Node<E> node = new Node<>(e);
        if (head == null) {
            head = node;
        }else {
            Node<E> n = head;
            head = node;
            head.next = n;
        }
        size++;
        return e;
    }

    @Override
    public E pop() {
        if (head == null) {
            return null;
        }
        E data = head.data;
        head = head.next;
        size--;
        return data;
    }

    @Override
    public E peek() {
        return head == null ? null : head.data;
    }

    @Override
    public int size() {
        return size;
    }

    private static class Node<E> {
        E data;
        Node<E> next;

        public Node(E e) {
            data = e;
        }
    }
}

　　

/**
 * 栈结构
 */
public interface Stack<E> {

    /**
     * 入栈
     * @param e 入栈元素
     * @return 入栈元素
     */
    E push(E e);

    /**
     * 将栈顶元素弹出
     * @return 栈顶元素
     */
    E pop();

    /**
     * 查看栈顶元素，该方法不会弹出栈顶元素
     * @return 栈顶元素
     */
    E peek();

    /**
     * 查看栈深度
     * @return 栈深度
     */
    int size();
}

　　

　　五、应用实例：简易计算器

　　在进入写代码之前需要知道的前置知识是：前缀表达式（也叫波兰表达式），中缀表达式和后缀表达式（也叫逆波兰表达式）。

　　前缀、中缀、后缀表达式是对表达式的不同记法，其区别在于运算符相对于操作数的位置不同，前缀表达式的运算符位于操作数之前，中缀和后缀同理

　　举例：
　　中缀表达式：1 + (2 + 3) × 4 - 5
　　前缀表达式：- + 1 × + 2 3 4 5
　　后缀表达式：1 2 3 + 4 × + 5 -

　　中缀表达式 中缀表达式是一种通用的算术或逻辑公式表示方法，操作符以中缀形式处于操作数的中间。中缀表达式是人们常用的算术表示方法。 虽然人的大脑很容易理解与分析中缀表达式，但对计算机来说中缀表达式却是很复杂的，因此计算表达式的值时，通常需要先将中缀表达式转换为前缀或后缀表达式，然后再进行求值。对计算机来说，计算前缀或后缀表达式的值非常简单。

　　我下面讲解的例子中是利用后缀表达式的算法来实现的，因此，代码中回涉及到 运算字符串转中缀表达式，中缀表达式转后缀表达式的过程。

　　后缀表达式步骤

　　从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 和 栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果。

　　例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:

　　1.从左至右扫描，将3和4压入堆栈；
　　2.遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
　　3.将5入栈；
　　4.接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
　　5.将6入栈；
　　6.最后是-运算符，计算出35-6的值，即29，由此得出最终结果

　　根据上面的步骤，我们可以使用代码来实现：

　

/**
     * 根据后缀表达式计算值
     * @param items 后缀表达式
     * @return 计算结果
     */
    public int calculate(List<String> items) {
        /**
         * 用于保存过程变量和操作符等
         */
        Stack<String> stack = new LinkStack<>();
        //便利
        for (String item : items) {
            //如果为数字，直接放入栈中
            if (item.matches("\\d+")) {
                stack.push(item);
            }else {
                //弹出栈顶元素进行运算
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res;
                switch (item) {
                    case "+" :
                        res = num1 + num2;
                        break;
                    case "-" :
                        res = num1 - num2;
                        break;
                    case "*" :
                        res = num1 * num2;
                        break;
                    case "/" :
                        res = num1 / num2;
                        break;
                    default:
                        throw new RuntimeException("非法的运算符：" + item);
                }
                //运算完将结果压入栈中
                stack.push("" + res);
            }
        }
        //整个表达式扫描结束后，此时栈中只剩一个元素，该元素即为结算结果，从栈中弹出即可
        return Integer.parseInt(stack.pop());
    }

　　测试结果：

 public static void main(String[] args) {
        Calculator calculator = new Calculator();
        List<String> items = new ArrayList<>();
        items.add("3");
        items.add("4");
        items.add("+");
        items.add("5");
        items.add("*");
        items.add("6");
        items.add("-");
        System.out.println(calculator.calculate(items));
    }

//结果：29

　　虽然后面可以计算出表达式的最终结果，但是的实际的应用中计算的表达式往往都是按照我们的计算习惯来书写的（即中缀表达式，如(3+4)×5-6）。因此，想要正确的得到结果我们需要再多一个步骤，就是人们习惯的计算方式的中缀表达式转换成对计算机友好的后缀表达式。具体步骤如下：　　

　　1）初始化两个栈：运算符栈s1和储存中间结果的栈s2；
　　2）从左至右扫描中缀表达式；
　　3）遇到操作数时，将其压s2；
　　4）遇到运算符时，比较其与s1栈顶运算符的优先级：
　　　　4.1）如果s1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
　　　　4.2）否则，若优先级比栈顶运算符的高，也将运算符压入s1；
　　　　4.3）否则，将s1栈顶的运算符弹出并压入到s2中，再次转到(4-1)与s1中新的栈顶运算符相比较；

　　5）遇到括号时：
　　　　5.1) 如果是左括号“(”，则直接压入s1
　　　　5.2) 如果是右括号“)”，则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，此时将这一对括号丢弃
　　6）重复步骤2至5，直到表达式的最右边
　　7）将s1中剩余的运算符依次弹出并压入s2
　　8）依次弹出s2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

　　具体代码如下：

　　（一）、解析算式

/**
     * 将表达式解析成List
     * @param expression 表达式
     * @return
     */
    private List<String> parseExpr(String expression) {
        char[] chars = expression.toCharArray();
        int len = chars.length;
        List<String> items = new ArrayList<>(len);
        int index = 0;
        while (index < len) {
            char c = chars[index];
            //数字
            if (c >= 48 && c <= 57) {
                String tmp = "";
                //操作数大于一位数，主要是通过判断下一位是否为数字
                while (index < chars.length && chars[index] >= 48 && chars[index] <= 57) {
                    tmp += chars[index];
                    index++;
                }
                items.add(tmp);
            }else {
                items.add(c + "");
                index++;
            }
        }
        return items;
    }

　　（二）、获取运算符的优先级

/**
     * 获取运算符的优先级，数字越大优先级越大
     * @param operateChar 运算符
     * @return 优先级
     */
    private int priority(String operateChar) {
        if ("*".equals(operateChar) || "/".equals(operateChar)) {
            return 2;
        }else if ("+".equals(operateChar) || "-".equals(operateChar)) {
            return 1;
        }else {
            //throw new RuntimeException("非法的操作符：" + operateChar);
            return 0;
        }
    }

　　

　　（三）、中缀转后缀表达式

/**
 * 1）初始化两个栈：运算符栈operateStack和储存中间结果的栈tmp；
 * 2）从左至右扫描中缀表达式；
 * 3）遇到操作数时，将其压tmp；
 * 4）遇到运算符时，比较其与operateStack栈顶运算符的优先级：
 * 　　4.1）如果operateStack为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
 * 　　4.2）否则，若优先级比栈顶运算符的高，也将运算符压入operateStack；
 * 　　4.3）否则，将operateStack栈顶的运算符弹出并压入到tmp中，再次转到(4-1)与operateStack中新的栈顶运算符相比较；
 * 5）遇到括号时：
 * 　　5.1) 如果是左括号“(”，则直接压入operateStack
 * 　　5.2) 如果是右括号“)”，则依次弹出operateStack栈顶的运算符，并压入tmp，直到遇到左括号为止，此时将这一对括号丢弃
 * 6）重复步骤2至5，直到表达式的最右边
 * 7）将operateStack中剩余的运算符依次弹出并压入tmp
 * 8）依次弹出tmp中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式
 * @param expr 中缀表达式
 * @return 后缀表达式
 */
public List<String> midfixToSuffix(String expr) {
    /**
     * 将表达式的操作数和运算符转换成集合
     */
    List<String> items = parseExpr(expr);
    //操作数栈
    Stack<String> operateStack = new LinkStack<>();
    //临时变量的保存集合，这里使用了List集合
    //如果用栈也可以实现，但是需要在最后将弹出栈元素的逆序进行运算
    //所以使用List集合避免了这个转换的问题
    List<String> tmp = new ArrayList<>();
    //操作的位置
    int index = 0;
    //表达式长度
    int len = items.size();
    while (index < len) {
        String item = items.get(index);
        //遇到操作数时，将其压tmp；
        if (item.matches("\\d+")) {
            tmp.add(item);
        }else if (item.equals("(")) {//如果是左括号“(”，则直接压入operateStack
            operateStack.push(item);
        } else if (item.equals(")")) {//如果是右括号“)”，则依次弹出operateStack栈顶的运算符，并压入tmp，直到遇到左括号为止，此时将这一对括号丢弃
            while (!operateStack.peek().equals("(")) {
                tmp.add(operateStack.pop());
            }
            //直接弹出栈顶元素即可
            operateStack.pop();
        } else {//遇到运算符时，比较其与operateStack栈顶运算符的优先级
            //如果operateStack为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
            if (operateStack.isEmpty() || "(".equals(operateStack.peek())) {
                operateStack.push(item);
            }else if (priority(item) > priority(operateStack.peek())) {//否则，若优先级比栈顶运算符的高，也将运算符压入operateStack；
                tmp.add(item);
            } else {//否则，将operateStack栈顶的运算符弹出并压入到tmp中，再次转到(4-1)与operateStack中新的栈顶运算符相比较；
                while (!operateStack.isEmpty() && priority(item) <= priority(operateStack.peek())) {
                    tmp.add(operateStack.pop());
                }
                //将运算符压入栈
                operateStack.push(item);
            }
        }
        //没一轮结束需要将操作位置往后移动一位
        index++;
    }
    //解析结束后需要将剩下的栈元素全部弹出来放入到tmp中
    while (!operateStack.isEmpty()) {
        tmp.add(operateStack.pop());
    }
    return tmp;
}

　　(四）、计算结果

/**
     * 根据后缀表达式计算值
     * @param items 后缀表达式
     * @return 计算结果
     */
    public int calculate(List<String> items) {
        /**
         * 用于保存过程变量和操作符等
         */
        Stack<String> stack = new LinkStack<>();
        //便利
        for (String item : items) {
            //如果为数字，直接放入栈中
            if (item.matches("\\d+")) {
                stack.push(item);
            }else {
                //弹出栈顶元素进行运算
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res;
                switch (item) {
                    case "+" :
                        res = num1 + num2;
                        break;
                    case "-" :
                        res = num1 - num2;
                        break;
                    case "*" :
                        res = num1 * num2;
                        break;
                    case "/" :
                        res = num1 / num2;
                        break;
                    default:
                        throw new RuntimeException("非法的运算符：" + item);
                }
                //运算完将结果压入栈中
                stack.push("" + res);
            }
        }
        //整个表达式扫描结束后，此时栈中只剩一个元素，该元素即为结算结果，从栈中弹出即可
        return Integer.parseInt(stack.pop());
    }

　　（五）、测试

public static void main(String[] args) {
        Calculator calculator = new Calculator();
        List<String> items = calculator.midfixToSuffix("(3+4)*5-6");
        System.out.println("后缀表达式为：" + items);
        int result = calculator.calculate(items);
        System.out.println("运算结果为： " + result);
    }

//后缀表达式为：[3, 4, +, 5, *, 6, -]
//运算结果为： 29

　　完整的代码如下：

public class Calculator {

    public static void main(String[] args) {
        Calculator calculator = new Calculator();
        List<String> items = calculator.midfixToSuffix("(3+4)*5-6");
        System.out.println("后缀表达式为：" + items);
        int result = calculator.calculate(items);
        System.out.println("运算结果为： " + result);
    }

    /**
     * 1）初始化两个栈：运算符栈operateStack和储存中间结果的栈tmp；
     * 2）从左至右扫描中缀表达式；
     * 3）遇到操作数时，将其压tmp；
     * 4）遇到运算符时，比较其与operateStack栈顶运算符的优先级：
     * 　　4.1）如果operateStack为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
     * 　　4.2）否则，若优先级比栈顶运算符的高，也将运算符压入operateStack；
     * 　　4.3）否则，将operateStack栈顶的运算符弹出并压入到tmp中，再次转到(4-1)与operateStack中新的栈顶运算符相比较；
     * 5）遇到括号时：
     * 　　5.1) 如果是左括号“(”，则直接压入operateStack
     * 　　5.2) 如果是右括号“)”，则依次弹出operateStack栈顶的运算符，并压入tmp，直到遇到左括号为止，此时将这一对括号丢弃
     * 6）重复步骤2至5，直到表达式的最右边
     * 7）将operateStack中剩余的运算符依次弹出并压入tmp
     * 8）依次弹出tmp中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式
     * @param expr 中缀表达式
     * @return 后缀表达式
     */
    public List<String> midfixToSuffix(String expr) {
        /**
         * 将表达式的操作数和运算符转换成集合
         */
        List<String> items = parseExpr(expr);
        //操作数栈
        Stack<String> operateStack = new LinkStack<>();
        //临时变量的保存集合，这里使用了List集合
        //如果用栈也可以实现，但是需要在最后将弹出栈元素的逆序进行运算
        //所以使用List集合避免了这个转换的问题
        List<String> tmp = new ArrayList<>();
        //操作的位置
        int index = 0;
        //表达式长度
        int len = items.size();
        while (index < len) {
            String item = items.get(index);
            //遇到操作数时，将其压tmp；
            if (item.matches("\\d+")) {
                tmp.add(item);
            }else if (item.equals("(")) {//如果是左括号“(”，则直接压入operateStack
                operateStack.push(item);
            } else if (item.equals(")")) {//如果是右括号“)”，则依次弹出operateStack栈顶的运算符，并压入tmp，直到遇到左括号为止，此时将这一对括号丢弃
                while (!operateStack.peek().equals("(")) {
                    tmp.add(operateStack.pop());
                }
                //直接弹出栈顶元素即可
                operateStack.pop();
            } else {//遇到运算符时，比较其与operateStack栈顶运算符的优先级
                //如果operateStack为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
                if (operateStack.isEmpty() || "(".equals(operateStack.peek())) {
                    operateStack.push(item);
                }else if (priority(item) > priority(operateStack.peek())) {//否则，若优先级比栈顶运算符的高，也将运算符压入operateStack；
                    tmp.add(item);
                } else {//否则，将operateStack栈顶的运算符弹出并压入到tmp中，再次转到(4-1)与operateStack中新的栈顶运算符相比较；
                    while (!operateStack.isEmpty() && priority(item) <= priority(operateStack.peek())) {
                        tmp.add(operateStack.pop());
                    }
                    //将运算符压入栈
                    operateStack.push(item);
                }
            }
            //没一轮结束需要将操作位置往后移动一位
            index++;
        }
        //解析结束后需要将剩下的栈元素全部弹出来放入到tmp中
        while (!operateStack.isEmpty()) {
            tmp.add(operateStack.pop());
        }
        return tmp;
    }

    /**
     * 获取运算符的优先级，数字越大优先级越大
     * @param operateChar 运算符
     * @return 优先级
     */
    private int priority(String operateChar) {
        if ("*".equals(operateChar) || "/".equals(operateChar)) {
            return 2;
        }else if ("+".equals(operateChar) || "-".equals(operateChar)) {
            return 1;
        }else {
            //throw new RuntimeException("非法的操作符：" + operateChar);
            return 0;
        }
    }

    /**
     * 将表达式解析成List
     * @param expression 表达式
     * @return
     */
    private List<String> parseExpr(String expression) {
        char[] chars = expression.toCharArray();
        int len = chars.length;
        List<String> items = new ArrayList<>(len);
        int index = 0;
        while (index < len) {
            char c = chars[index];
            //数字
            if (c >= 48 && c <= 57) {
                String tmp = "";
                //操作数大于一位数，主要是通过判断下一位是否为数字
                while (index < chars.length && chars[index] >= 48 && chars[index] <= 57) {
                    tmp += chars[index];
                    index++;
                }
                items.add(tmp);
            }else {
                items.add(c + "");
                index++;
            }
        }
        return items;
    }

    /**
     * 根据后缀表达式计算值
     * @param items 后缀表达式
     * @return 计算结果
     */
    public int calculate(List<String> items) {
        /**
         * 用于保存过程变量和操作符等
         */
        Stack<String> stack = new LinkStack<>();
        //便利
        for (String item : items) {
            //如果为数字，直接放入栈中
            if (item.matches("\\d+")) {
                stack.push(item);
            }else {
                //弹出栈顶元素进行运算
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res;
                switch (item) {
                    case "+" :
                        res = num1 + num2;
                        break;
                    case "-" :
                        res = num1 - num2;
                        break;
                    case "*" :
                        res = num1 * num2;
                        break;
                    case "/" :
                        res = num1 / num2;
                        break;
                    default:
                        throw new RuntimeException("非法的运算符：" + item);
                }
                //运算完将结果压入栈中
                stack.push("" + res);
            }
        }
        //整个表达式扫描结束后，此时栈中只剩一个元素，该元素即为结算结果，从栈中弹出即可
        return Integer.parseInt(stack.pop());
    }

}

　　

　　简单的计算器基本已经写完了。如果你感兴趣的话，可以将上面的代码拿下来自己显现更多的功能，比如说支持小数，其他的运算，表达式中允许有空格等。这些功能实现起来是不难的，只要在上面的基础上做一些改动即可。