图-最短路-dijkstra-0/1BFS-1368. 使网格图至少有一条有效路径的最小代价

2020-03-01 22:59:59

问题描述：

给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字，对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况：

• 1 ，下一步往右走，也就是你会从 grid[i][j] 走到 grid[i][j + 1]
• 2 ，下一步往左走，也就是你会从 grid[i][j] 走到 grid[i][j - 1]
• 3 ，下一步往下走，也就是你会从 grid[i][j] 走到 grid[i + 1][j]
• 4 ，下一步往上走，也就是你会从 grid[i][j] 走到 grid[i - 1][j]

注意网格图中可能会有 无效数字 ，因为它们可能指向 grid 以外的区域。

一开始，你会从最左上角的格子 (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0) 出发，每一步都顺着数字对应方向走，最终在最右下角的格子 (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。

你可以花费 cost = 1 的代价修改一个格子中的数字，但每个格子中的数字 只能修改一次 。

请你返回让网格图至少有一条有效路径的最小代价。

示例 1：

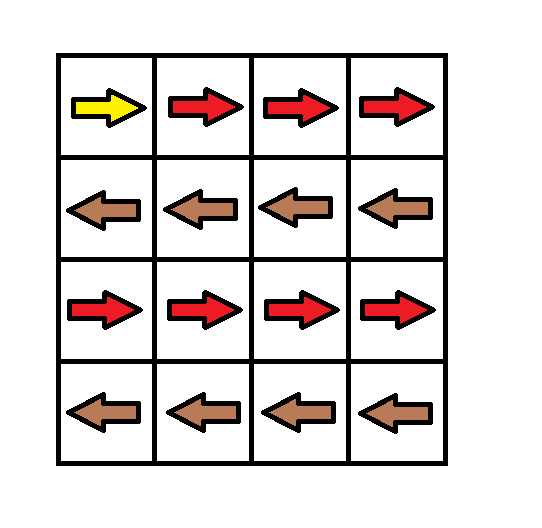
输入：grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
输出：3
解释：你将从点 (0, 0) 出发。
到达 (3, 3) 的路径为： (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) 花费代价 cost = 1 使方向向下 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) 花费代价 cost = 1 使方向向下 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) 花费代价 cost = 1 使方向向下 --> (3, 3)
总花费为 cost = 3.

示例 2：

输入：grid = [[1,1,3],[3,2,2],[1,1,4]]
输出：0
解释：不修改任何数字你就可以从 (0, 0) 到达 (2, 2) 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100

问题求解：

最重要的是reduce，如何将问题转成已知的知识非常重要。

本题中看似是需要求改变方向个数最少，其实是在最短路径。

如果我们将通过标示到达w = 0，那么通过修改到达的w = 1。

解法一：dijkstra

朴素的dijkstra算法的时间复杂度为O(V ^ 2)；如果使用优先队列和邻接表可以将时间复杂度优化为O((E + V)logV)。

时间复杂度：O(mnlog(mn))

    int[][] dirs = new int[][]{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

    public int minCost(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[] dist = new int[m * n];
        Arrays.fill(dist, (int)(1e9));
        PriorityQueue<int[]> pq = new PriorityQueue<>((int[] o1, int[] o2) -> o1[1] - o2[1]);
        int[] used = new int[m * n];
        pq.add(new int[]{0, 0});
        while (!pq.isEmpty()) {
            int[] node = pq.poll();
            int from = node[0];
            int d = node[1];
            if (used[from] == 1) continue;
            used[from] = 1;
            dist[from] = d;
            int x = from / n;
            int y = from % n;
            for (int i = 1; i <= 4; i++) {
                int nx = x + dirs[i - 1][0];
                int ny = y + dirs[i - 1][1];
                if (nx >= m || nx < 0 || ny >= n || ny < 0) continue;
                int w = grid[x][y] == i ? 0 : 1;
                int to = nx * n + ny;
                if (dist[to] > dist[from] + w) {
                    dist[to] = dist[from] + w;
                    pq.add(new int[]{to, dist[to]});
                }
            }
        }
        return dist[m * n - 1];
    }

解法二：0-1BFS

本题有个特殊的地方就是边权重只为0 / 1，在这样的图上求解最短路径的最优解是使用0-1 BFS。

0-1BFS使用了BFS的性质，当前层和下一层的节点的距离最大不超过1，因此当我们碰到w = 0的节点的时候可将其加入队首，如果碰到w = 1的节点的时候将其加入队尾，这样就巧妙的进行了排序工作，因此时间复杂度要更优。

时间复杂度：O(mn)

    int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    public int minCost(int[][] grid) {
        int res = 0;
        int m = grid.length;
        int n = grid[0].length;
        if (m == 1 && n == 1) return res;
        Deque<int[]> q = new LinkedList<>();
        Set<Integer> used = new HashSet<>();
        q.add(new int[]{0, 0});
        while (!q.isEmpty()) {
            int[] curr = q.pollFirst();
            if (used.contains(curr[0])) continue;
            used.add(curr[0]);
            int x = curr[0] / n;
            int y = curr[0] % n;
            int cost = curr[1];
            if (x == m - 1 && y == n - 1) return cost;
            for (int i = 1; i <= 4; i++) {
                int nx = x + dirs[i - 1][0];
                int ny = y + dirs[i - 1][1];
                if (nx < 0 || nx >= m || ny < 0 || ny >= n || used.contains(nx * n + ny)) continue;
                if (grid[x][y] == i)
                    q.addFirst(new int[]{nx * n + ny, cost});
                else
                    q.addLast(new int[]{nx * n + ny, cost + 1});
            }
        }
        return -1;
    }