最大比率传输（Maximum Ratio Transmission， MRT）原理分析

转载请注明出处。

最大比率发射（Maximum Ratio Transmission， MRT）是文献中经常看见的一个词，今天就在这里做一下笔记。

参考文献为:T. K. Y. Lo, "Maximum ratio transmission," in IEEE Transactions on Communications, vol. 47, no. 10, pp. 1458-1461, Oct. 1999. doi: 10.1109/26.795811

1. 背景

无线通信系统受到的最不利的传播影响是多径衰落。天线分集技术是无线通信工程师对抗多径衰落的常用方法之一。一种经典的组合技术是最大比率组合（MRC），MRC中来自接收天线单元的信号被加权，使得其和的信噪比（SNR）最大。目前为止，MRC技术仅用于接收应用处理中。随着越来越多的无线业务的出现，越来越多的应用可能需要在发射机或发射机和接收机处进行分集以对抗严重的衰落效应。因此提出了一些方案，比如延迟发射分集方案。

然而，这些发射分集技术建立在目标的基础上，而不是最大化信噪比。也就是说，就信噪比性能而言，它们是次优的。因此，本文将从概念和原理上建立最大传动比（MRT）的框架。它可以看作是多发射天线和多接收天线最大比值算法的推广。它还为系统利用发射分集和接收分集获得最佳性能提供了参考。

2. 系统模型

发射端配备 \(K\) 根天线，接收端配备 \(L\) 根发射天线，其系统模型如图1所示：

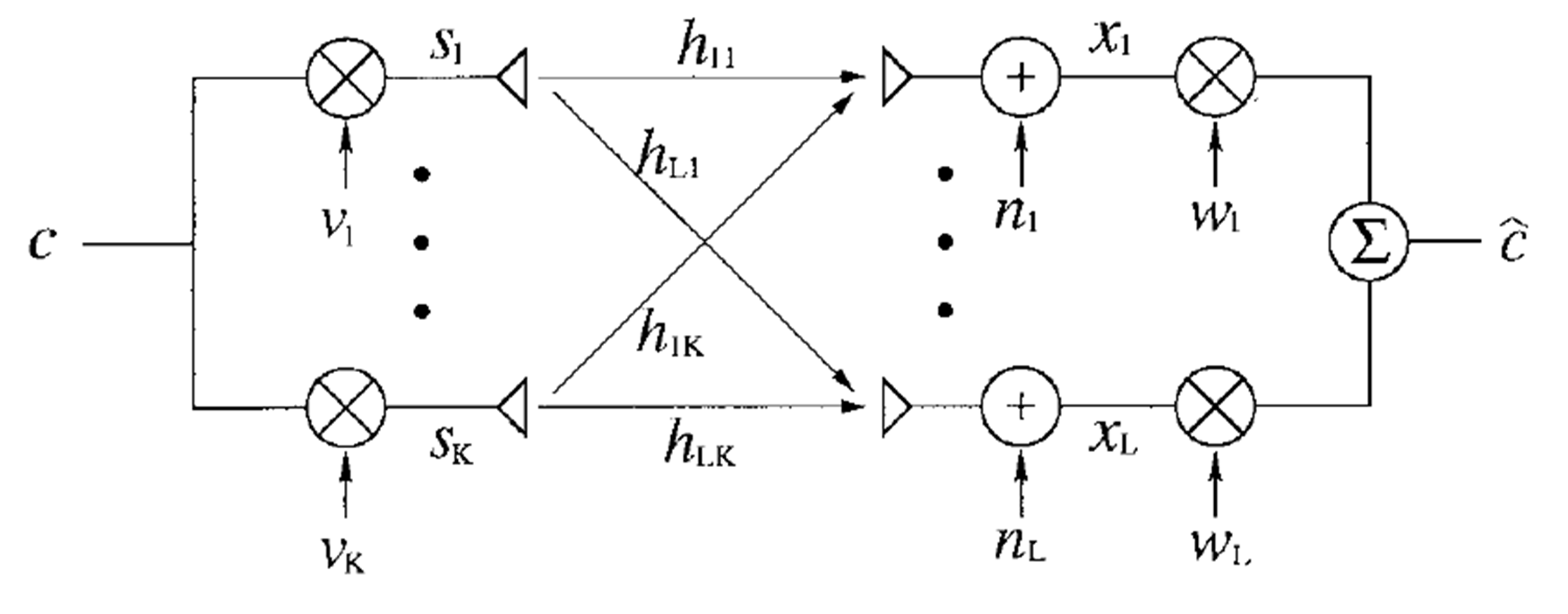图1. 系统模型

假设其信道 \(\pmb{H}\) 是统计信道，可以表示为：

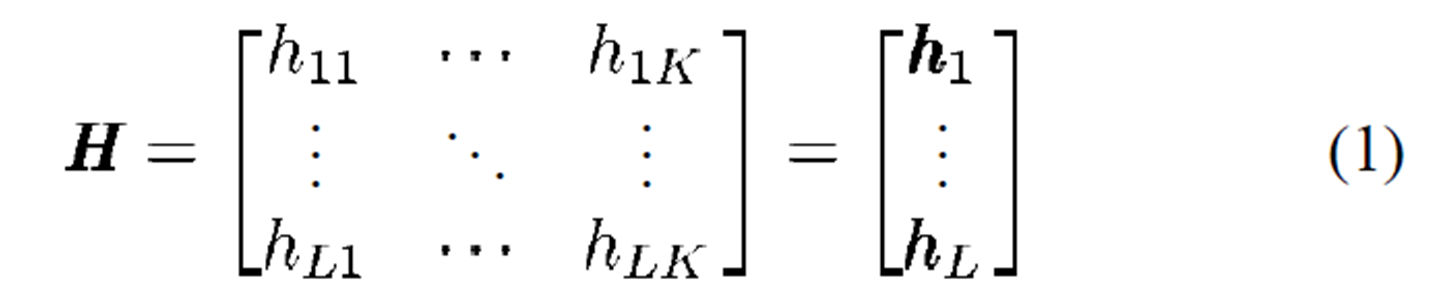
这里 \(h_{pk}\) 表示第 \(k\) 根天线和第 \(p\) 根天线的信道系数。

\[{\pmb{x}} = {\boldsymbol{Hs}} + {\boldsymbol{n}} \quad \quad \quad \quad \quad(2)
\]

这里发射的信号 \(\boldsymbol{s}\) 表示为

\[{\pmb{s}} = {[{s_1} \cdots {s_K}]^{\rm T}} = c{[{v_1} \cdots {v_K}]^{\rm T}}
\]

\({\pmb{n}} = {[{n_1} \cdots {n_L}]^{\rm T}}\) 表示加性高斯白噪声。

3. 最大比率发射（MRT）原理

为了从信道矩阵生成 \(K \times 1\) 的传输权重向量，需要进行线性变换，即:

\[{\pmb{v}} = \frac{1}{a}{({\pmb{gH}})^{\rm H}}
\]

这里 \({\pmb{g}} = [{g_1} \cdots {g_L}]\)。传输信号向量就可以表示为：

\[{\pmb{s}} = \frac{c}{a}{({\pmb{gH}})^{\rm H}}
\]

归一化因子 \(a\) 必须满足：

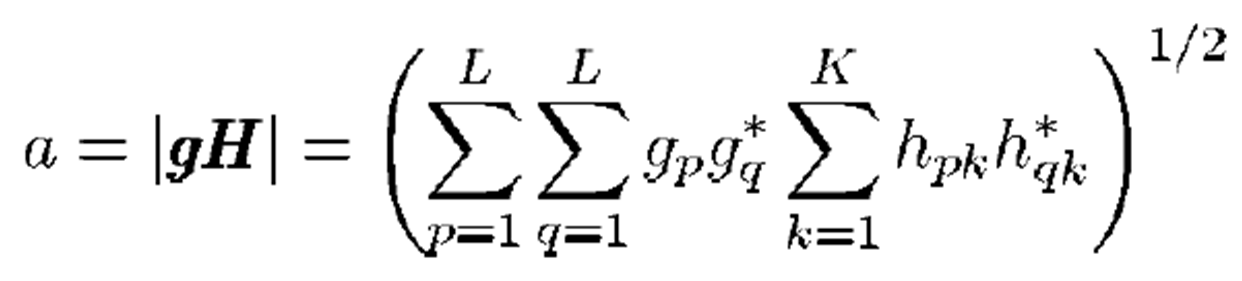
因此，接收信号变为：

\[{\pmb{x}} = \frac{c}{a}{\pmb{H}}{({\pmb{gH}})^{\rm H}} + {\pmb{n}}
\]

为了估计发送符号，必须将接收权重向量 \(\pmb{w}\) 应用于接收信号向量 \(\pmb{x}\)，如果将 \(\pmb{w}\) 设为 \(\pmb{g}\)，那么估计的符号为：

\[\tilde c = {\pmb{gx}} = \frac{c}{a}{\pmb{gH}}{({\pmb{gH}})^{\rm H}} + {\pmb{gH}} = ac + {\pmb{gn}}
\]

总的SNR为：

\[\gamma = \frac{{{a^2}}}{{{\pmb{g}}{{\pmb{g}}^{\rm H}}}}{\gamma _0} = \frac{{{a^2}{\gamma _0}}}{{\sum\limits_{p = 1}^L {{{\left| {{g_p}} \right|}^2}} }}\quad \quad \quad\quad\quad(10)
\]

这里 \({\gamma _0} = \frac{{\sigma _c^2}}{{\sigma _n^2}}\) 表示单发射天线的平均SNR，（即没有分集）。

从（10）式可知，总SNR和 \(\pmb{g}\) 有关，因此，可以通过选择合适的 \(\pmb{g}\) 来最大化总的SNR。

由于 \(h_{pk}\) 假设在统计意义上是相同的，所以最大化SNR必须满足 \(\left| {{g_1}} \right| = \left| {{g_2}} \right| = \cdots = \left| {{g_L}} \right|\)。在不改变问题性质的情况下，为了简单起见，可以设置 \(\left| {{g_p}} \right| = 1\)，因此，总的SNR可以表示为：

\[\gamma = \frac{{{a^2}}}{L}{\gamma _0} \quad \quad\quad \quad\quad \quad （11）
\]

所以，当 \({{a^2}}\) 最大时，（11）式就是最大值。那么 \({{a^2}}\) 时就有：

\[{({g_p}g_q^*)^*} = \frac{{\sum\limits_{k = 1}^K {{h_{pk}}h_{qk}^*} }}{{\left| {\sum\limits_{k = 1}^K {{h_{pk}}h_{qk}^*} } \right|}}
\]

此时，有：

\[{a^2} = \sum\limits_{p = 1}^L {\sum\limits_{q = 1}^L {\left| {\sum\limits_{k = 1}^K {{h_{pk}}h_{qk}^*} } \right|} }
\]

4. 讨论

往期精选：

[1] 线性降维：主成分分析PCA原理分析与仿真验证

[2] 5G+AI：有哪些新的研究方向和新范式？

[3] 简述3D点云配准算法

[4] 5G为人工智能与工业互联网赋能|79页高清PPT

[5] 智能算法|以动物命名的算法

[6] 一份超全面的机器学习公共数据集

[7] 矩阵填充|奇异值阈值算法

[8] 可重构/大规模智能反射表面reconfigurable/large intelligent surface综述

[9] 迭代硬阈值类算法总结||IHT/NIHT/CGIHT/HTP

[10] 软阈值迭代算法（ISTA）和快速软阈值迭代算法（FISTA）

[11] 伍德伯里矩阵恒等式（Woodbury matrix identity）

[12] 压缩感知：一种新型亚采样技术

更多精彩内容请关注订阅号优化与算法和加入QQ讨论群1032493483获取更多资料