LeetCode——221. 最大正方形

221. 最大正方形

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

输入: 

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出: 4

https://leetcode-cn.com/problems/maximal-square/

暴力法：

把数组中每一个点都当成正方形的左顶点来向右下方扫描，来寻找最大正方形。

具体的扫描方法是，确定了左顶点后，再往下扫的时候，正方形的竖边长度就确定了，只需要找到横边即可，这时候我们使用直方图的原理，从其累加值能反映出上面的值是否全为1。

通过这种方法我们就可以找出最大的正方形，参见代码如下：

c++

class Solution {
public:
    int maximalSquare(vector<vector<char> >& matrix) {
        int res = 0;
        for (int i = 0; i < matrix.size(); ++i) {
            vector<int> v(matrix[i].size(), 0);
            for (int j = i; j < matrix.size(); ++j) {
                for (int k = 0; k < matrix[j].size(); ++k) {
                    if (matrix[j][k] == '1') ++v[k];
                }
                res = max(res, getSquareArea(v, j - i + 1));
            }
        }
        return res;
    }
    int getSquareArea(vector<int> &v, int k) {
        if (v.size() < k) return 0;
        int count = 0;
        for (int i = 0; i < v.size(); ++i) {
            if (v[i] != k) count = 0;
            else ++count;
            if (count == k) return k * k;
        }
        return 0;
    }
};

累加法：

下面这个方法用到了建立累计和数组的方法。

原理是建立好了累加和数组后，我们开始遍历二维数组的每一个位置，对于任意一个位置 (i, j)，我们从该位置往 (0,0) 点遍历所有的正方形，正方形的个数为 min(i,j)+1，由于我们有了累加和矩阵，能快速的求出任意一个区域之和，所以我们能快速得到所有子正方形之和，比较正方形之和跟边长的平方是否相等，相等说明正方形中的数字均为1，更新 res 结果即可，参见代码如下：

c++

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int m = matrix.size(), n = matrix[0].size(), res = 0;
        vector<vector<int>> sum(m, vector<int>(n, 0));
        for (int i = 0; i < matrix.size(); ++i) {
            for (int j = 0; j < matrix[i].size(); ++j) {
                int t = matrix[i][j] - '0';
                if (i > 0) t += sum[i - 1][j];
                if (j > 0) t += sum[i][j - 1];
                if (i > 0 && j > 0) t -= sum[i - 1][j - 1];
                sum[i][j] = t;
                int cnt = 1;
                for (int k = min(i, j); k >= 0; --k) {
                    int d = sum[i][j];
                    if (i - cnt >= 0) d -= sum[i - cnt][j];
                    if (j - cnt >= 0) d -= sum[i][j - cnt];
                    if (i - cnt >= 0 && j - cnt >= 0) d += sum[i - cnt][j - cnt];
                    if (d == cnt * cnt) res = max(res, d);
                    ++cnt;
                }
            }
        }
        return res;
    }
};

动态规划：

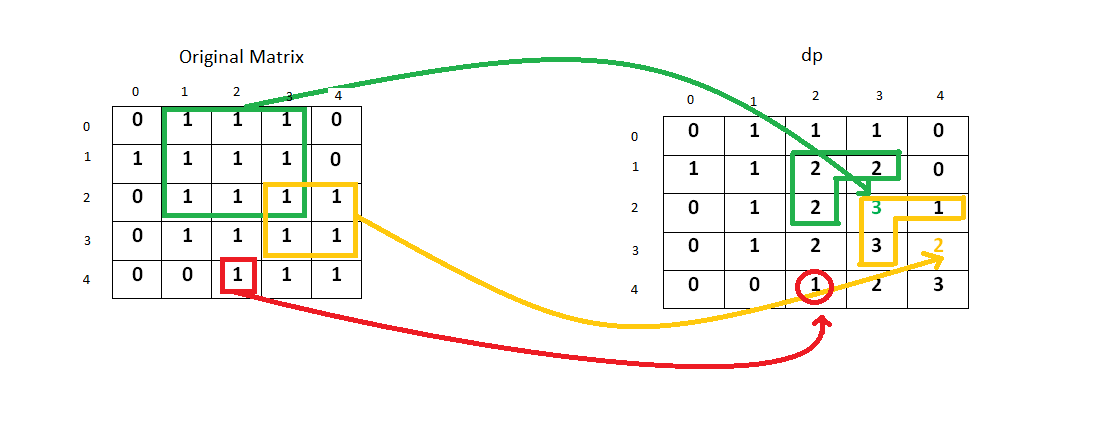
我们还可以进一步的优化时间复杂度到 O(n^2)，做法是使用 DP，建立一个二维 dp 数组，其中 dp[i][j] 表示到达 (i, j) 位置所能组成的最大正方形的边长。

首先来考虑边界情况，也就是当 i 或 j 为0的情况，那么在首行或者首列中，必定有一个方向长度为1，那么就无法组成长度超过1的正方形，最多能组成长度为1的正方形，条件是当前位置为1。边界条件处理完了，再来看一般情况的递推公式怎么办，对于任意一点 dp[i][j]，由于该点是正方形的右下角，所以该点的右边，下边，右下边都不用考虑，关心的就是左边，上边，和左上边。这三个位置的dp值 suppose 都应该算好的，还有就是要知道一点，只有当前 ( i , j ) 位置为1，dp[i] [j] 才有可能大于0，否则 dp[i][j] 一定为0。当 ( i , j ) 位置为1，此时要看 dp[i-1] [j-1], dp[i] [j-1]，和 dp[i-1] [j] 这三个位置，我们找其中最小的值，并加上1，就是 dp[i][j] 的当前值了，这个并不难想，毕竟不能有0存在，所以只能取交集，最后再用 dp[i][j] 的值来更新结果 res 的值即可，参见代码如下：

c++

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int m = matrix.size(), n = matrix[0].size(), res = 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || j == 0) dp[i][j] = matrix[i][j] - '0';
                else if (matrix[i][j] == '1') {
                    dp[i][j] = min(dp[i - 1][j - 1],
                                   min(dp[i][j - 1], dp[i - 1][j])) + 1;
                }
                res = max(res, dp[i][j]);
            }
        }
        return res * res;
    }
};

java

public class Solution {
    public int maximalSquare(char[][] matrix) {
        int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
        int[][] dp = new int[rows + 1][cols + 1];
        int maxsqlen = 0;
        for (int i = 1; i <= rows; i++) {
            for (int j = 1; j <= cols; j++) {
                if (matrix[i-1][j-1] == '1'){
                    dp[i][j] = Math.min(Math.min(dp[i][j - 1], dp[i - 1][j]),
                                        dp[i - 1][j - 1]) + 1;
                    maxsqlen = Math.max(maxsqlen, dp[i][j]);
                }
            }
        }
        return maxsqlen * maxsqlen;
    }
}

python

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        if(not matrix):
            return 0
        m=len(matrix)
        n=len(matrix[0])
        res=0
        dp=[[0]*(n+1) for _ in range(m+1)]
        for i in range(1,m+1):
            for j in range(1,n+1):
                if(matrix[i-1][j-1]=="1"):
                    dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])+1
                    res=max(dp[i][j],res)
        return res*res

动态规划优化：

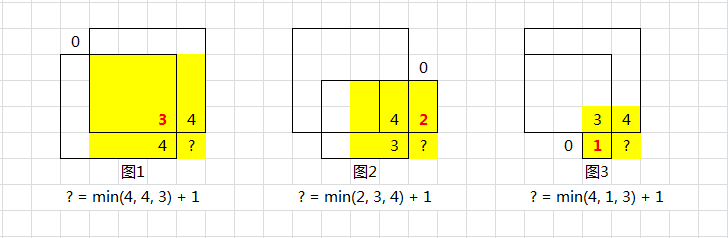
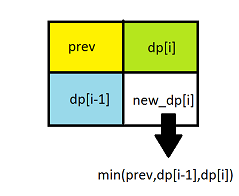
下面这种解法进一步的优化了空间复杂度，此时只需要用一个一维数组就可以解决，为了处理边界情况，padding 了一位，所以 dp 的长度是 m+1，然后还需要一个变量 pre 来记录上一个层的 dp 值，我们更新的顺序是行优先，就是先往下遍历，用一个临时变量t保存当前 dp 值，然后看如果当前位置为1，则更新 dp[i] 为 dp[i], dp[i-1], 和 pre 三者之间的最小值，再加上1，来更新结果 res，如果当前位置为0，则重置当前 dp 值为0，因为只有一维数组，每个位置会被重复使用，参见代码如下：

c++

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int m = matrix.size(), n = matrix[0].size(), res = 0, pre = 0;
        vector<int> dp(m + 1, 0);
        for (int j = 0; j < n; ++j) {
            for (int i = 1; i <= m; ++i) {
                int t = dp[i];
                if (matrix[i - 1][j] == '1') {
                    dp[i] = min(dp[i], min(dp[i - 1], pre)) + 1;
                    res = max(res, dp[i]);
                } else {
                    dp[i] = 0;
                }
                pre = t;
            }
        }
        return res * res;
    }
};

java

public class Solution {
    public int maximalSquare(char[][] matrix) {
        int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
        int[] dp = new int[cols + 1];
        int maxsqlen = 0, prev = 0;
        for (int i = 1; i <= rows; i++) {
            for (int j = 1; j <= cols; j++) {
                int temp = dp[j];
                if (matrix[i - 1][j - 1] == '1') {
                    dp[j] = Math.min(Math.min(dp[j - 1], prev), dp[j]) + 1;
                    maxsqlen = Math.max(maxsqlen, dp[j]);
                } else {
                    dp[j] = 0;
                }
                prev = temp;
            }
        }
        return maxsqlen * maxsqlen;
    }
}

python

class Solution:
    def maximalSquare(self, matrix: List[List[str]]) -> int:
        if(not matrix):
            return 0
        m=len(matrix)
        n=len(matrix[0])
        res=0
        pre=0
        dp=[0]*(n+1)
        for i in range(0,m):
            for j in range(1,n+1):
                tmp=dp[j]
                if(matrix[i][j-1]=="1"):
                    dp[j]=min(pre,dp[j-1],dp[j])+1
                    res=max(dp[j],res)
                else:
                    dp[j]=0
                pre=tmp
            pre=0
        return res*res